Michał Kucab Rzeszów 07.11.08r
Maciek Kościński
EF-DI 1 L06
Sprawozdanie z lab. 2
Badanie sygnałów dyskretnych z wykorzystaniem przekształcenia Z
Wyznaczyć transformaty Z i narysować wykresy następujących funkcji
a) f1=(n-1)
![]()
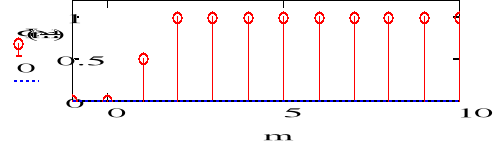
b) f2(n)=(n)+(n-2)
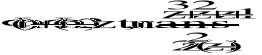
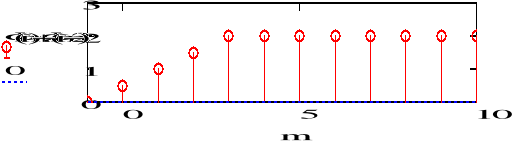
c) f3(n)=(n) - (n-4)

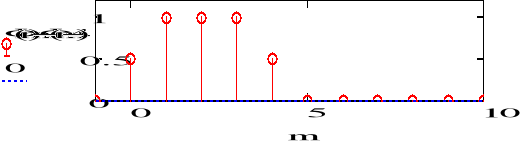
d) f4(n)=(n-1) * (n-3)
![]()
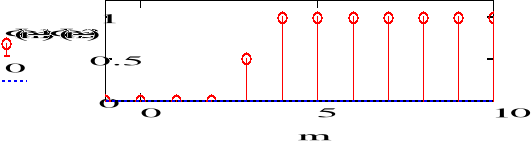
Wyznaczyć transformaty Z i narysować wykresy następujących funkcji
a) f1=(n-1)
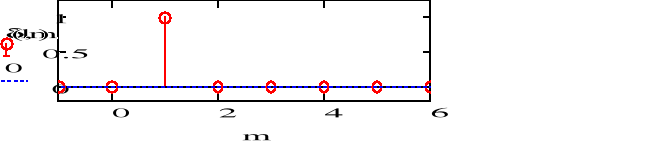
b) f2(n)=(n)+(n-2)
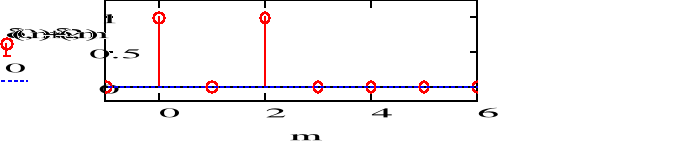
c) f3(n)=3(n) +2(n-1) - (n-3)

Wyznaczyć transformaty Z i narysować wykresy następujących funkcji
a) f1(n)=(0.25)n
![]()
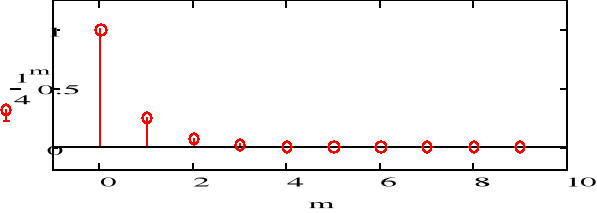
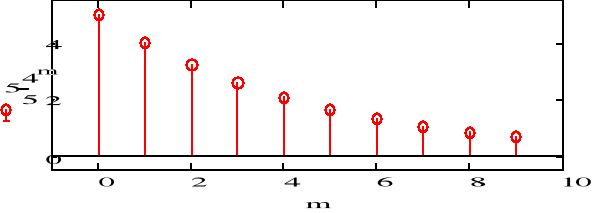
b) f2(n)=5(0.8)n
![]()
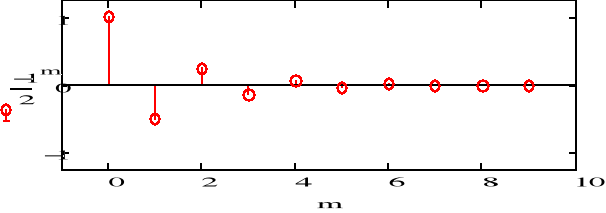
c) f3(n)=(-0.5)n
![]()
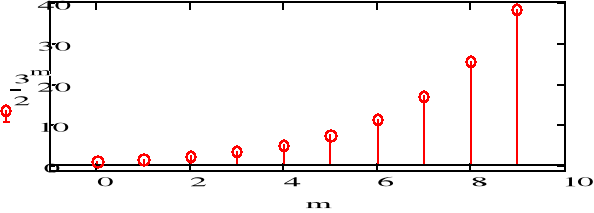
d) f4(n)=(1.5)n
![]()
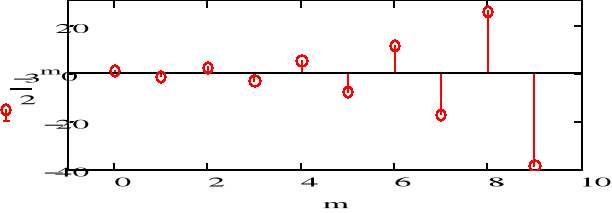
e) f5(n)=(-1.5)n
![]()
f) f6(n)=n
![]()
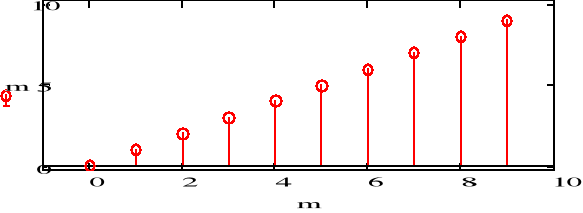
Wyznaczyć odwrotne transformaty Z i narysować wykresy następujących funkcji
a) F(z)=1/z
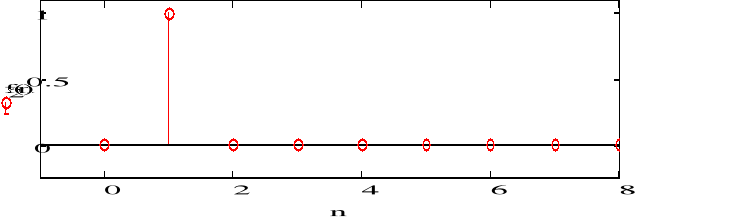
![]()
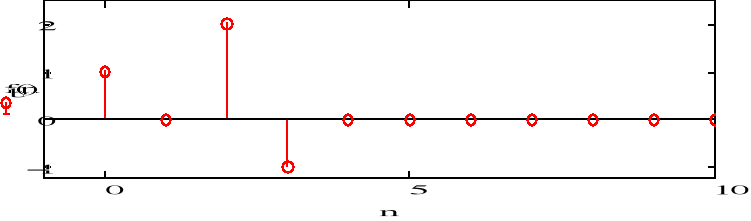
b) F(z)=1+2z-2 -z-3
![]()
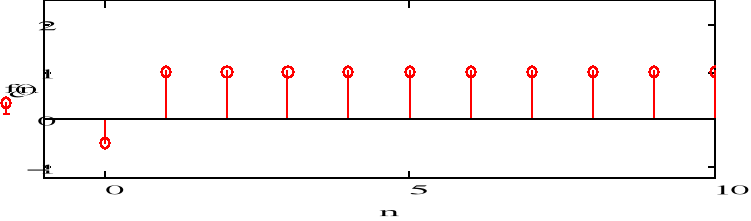
c) F(z)=1/(z-1)
![]()
d) F(z)=z-2/(z-1)
![]()
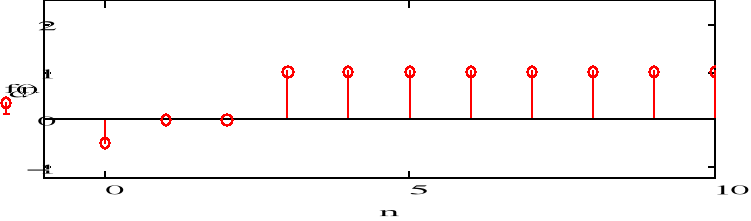
e) F(z)=z/(z-1)(z-1)
![]()
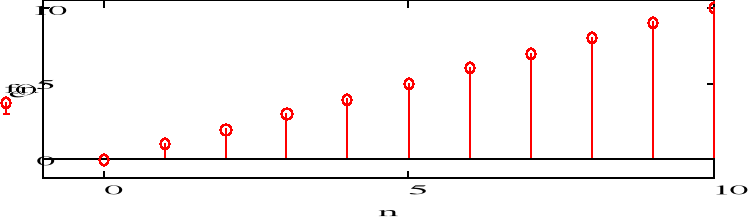
f) F(z)=z2/(z-1/3)(z-1/5)
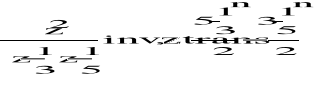
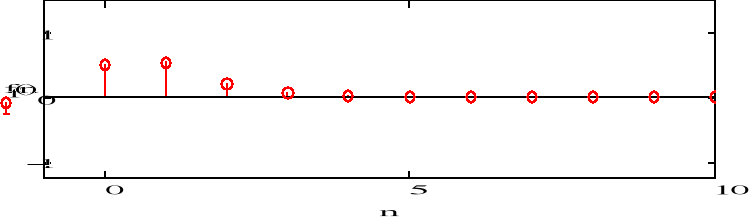
g) F(z)=10z/(z-1/2)(z-1/5)
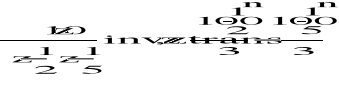
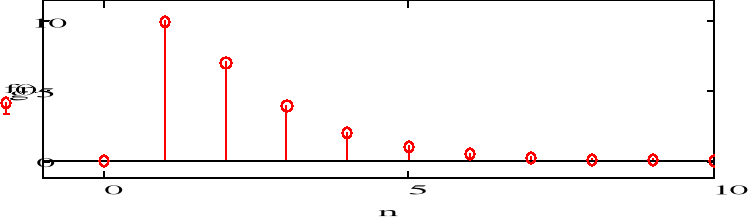
h) F(z)=1/(z-2)(z+3)
![]()
Wnioski :
Ad. 1
Jak zmienia się kształt sygnału oraz jego położenie względem podstawowego skoku jednostkowego?
Kształt sygnału zmienia się w zależności od wartości, którą podajemy przed skokiem jednostkowym, natomiast położenie sygnału zmienia sie w zależności od wartości przesunięcia względem punktu 0.
Ad. 2
Jak zmienia się kształt sygnału oraz jego położenie względem Delty podstawowej δ(n) (nieprzesuniętej)?
Kształt sygnału zmienia się w zależności od ilości delt, które dodajemy lub odejmujemy np. W podpunkcie a) mamy jedną Deltę Kronecker'a więc sygnał przyjmuje wartość różną od zera w tylko jednym miejscu zaś w c) mamy trzy Delty (przesunięte o różne wartości) i na wykresie można zauważyć, że sygnał przyjmuje wartości różne od zera w trzech miejscach. Położenie zaś zmienia sie podobnie jak w skoku jednostkowym, czyli w zależności od wartości przesunięcia względem 0.
Ad. 3
Jak zmienia się kształt sygnału?
Kształt sygnału zmienia się w zależności od podstawy funkcji wykładniczej (a):
1) a<-1 - dla potęg parzystych sygnał przyjmuje wartości dodatnie, które ze wzrostem argumentu dążą do 0, zaś dla potęg nieparzystych sygnał przyjmuje wartości ujemne, które również wraz ze wzrostem argumentu dążą do 0.
2) -1<a<0 - dla potęg parzystych sygnał przyjmuje wartości dodatnie, które ze wzrostem argumentu rosną, zaś dla potęg nieparzystych sygnał przyjmuje wartości ujemne, które ze wzrostem argumentu maleją.
3) 0<a<1 - sygnał malejący.
4) a>1 - sygnał rosnący.
Wyszukiwarka