WSTĘP
Jestem nauczycielem matematyki w szkole średniej. Od początku swojej pracy zawodowej dzielę się swoją wiedzą, umiejętnościami i doświadczeniem z innymi pracownikami szkoły. Dzielenie się wiedzą w zakresie dydaktyki przedmiotu i moimi doświadczeniami w nauczaniu matematyki odbywa się głownie podczas organizowanych przeze mnie od lat lekcji otwartych, na które zapraszam nauczycieli zespołu matematyczno - fizyczno - chemicznego i przedstawicieli innych zespołów. Po takich lekcjach udostępniam swoje materiały dydaktyczne, z których nauczyciele matematyki chętnie korzystają. Często nauczyciele innych przedmiotów czerpią pomysły do swoich lekcji.
Proponuję konspekt lekcji „Rozwiązywanie zadań z zastosowaniem własności ciągu arytmetycznego i geometrycznego”.
KONSPEKT LEKCJI
Klasa: II szkoły średniej
Przedmiot: matematyka
Nauczyciel: Ewa Szatkowska
Miejsce prowadzenia hospitacji: pracownia matematyczna
Temat lekcji: Rozwiązywanie zadań z zastosowaniem własności ciągu
arytmetycznego i geometrycznego.
Cele lekcji:
Uczeń potrafi:
rozpoznać ciąg arytmetyczny i geometryczny w zadaniach typowych i nietypowych
utworzyć kolejne wyrazy ciągu arytmetyczny i geometryczny, znając pierwszy wyraz i różnicę lub iloraz
stosować wzory dla ciągu arytmetyczny i geometryczny w zadaniach typowych i nietypowych
Metody:
rozmowa kierowana
praca z kartą pracy
Formy pracy:
zbiorowa jednolita
indywidualna jednolita
Środki i materiały dydaktyczne:
karta pracy ucznia - załącznik nr 4
przygotowane wykresy
Przebieg lekcji:
Przypomnienie podstawowych wiadomości dotyczących ciągu arytmetycznego i geometrycznego
Podanie tematu lekcji: „Rozwiązywanie zadań z zastosowaniem własności ciągu arytmetycznego i geometrycznego”
Podanie celów lekcji
Praca zbiorowa - rozwiązanie zadania 1 (uczniowie rozwiązują zadanie dwoma sposobami: nie używając wzorów na ciąg arytmetyczny i z zastosowaniem tych wzorów) - załącznik nr1
Praca zbiorowa - rozwiązanie zadania 2 (uczniowie rozwiązują zadanie dwoma sposobami: nie używając wzorów na ciąg arytmetyczny i z zastosowaniem tych wzorów; uczniowie korzystają przy rozwiązaniu z przygotowanych wykresów) - załącznik nr2
Praca zbiorowa - rozwiązanie zadania 3a (uczniowie rozwiązują zadanie dwoma sposobami: nie używając wzorów na ciąg geometryczny i z zastosowaniem tych wzorów) - załącznik nr3
Podsumowanie lekcji - praca indywidualna - rozwiązanie zadania 4 (uczniowie poprawiane i ocienione rozwiązania otrzymają na następnej lekcji)
Opracowała:
Ewa Szatkowska
Załącznik nr1
ZADANIE 1
Składając do kasy oszczędności, w każdym miesiącu o 20zł więcej niż w poprzednim uzbieramy po n miesiącach 1845zł. Oblicz liczbę miesięcy n, jeżeli pierwszy wkład wynosił 125zł.
I sposób rozwiązania zadania
1 wkład 125zł
2 wkład 125zł+20zł=145zł
3 wkład 145zł+20zł=165zł
4 wkład 165zł+20zł=185zł
5 wkład 185zł+20zł=205zł
6 wkład 205zł+20zl=225zł
7 wkład 225zł+20zł=245zl
8 wkład 245zl+20zł=265zł
9 wkład 265zł+20zł=285zł
Razem po 9 miesiącach 125+145+165+185+205+225+245+265+285=1845zł
II sposób rozwiązania zadania (stosowanie wiadomości dotyczących ciągu arytmetycznego)
Analiza zadania
Dane: a1=125 (pierwsza wpłata); r=20 (zwiększanie wpłaty); Sn=1845 (suma oszczędności)
Szukane: n- ilość miesięcy (miesięcy jest liczbę naturalną dodatnią)
Obliczenia
![]()
wzór na sumę n-początkowych wyrazów ciągu arytmetycznego
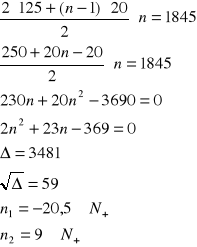
Ilość miesięcy n wynosi 9.
Załącznik nr2
ZADANIE 2
Temperatura w górach obniża się latem o 0,7ºC na każde 100m wzniesienia. Oblicz:
Temperaturę na Giewoncie (1900m), gdy w Zakopanym (837m) jest 16,4ºC.
Temperaturę nad Morskim Okiem (1393m), gdy na Rysach (2503m) jest 8,7ºC.
I sposób rozwiązania zadania 2a
Uczniowie nanoszą dane na wykres
1 Zakopane 837m temperatura 16,4
2 937m temperatura 16,4-0,7=15,7
3 1037m temperatura 15,7-0,7=15
4 1137m temperatura 15-0,7=14,3
5 1237m temperatura 14,3-0,7=13,6
6 1337m temperatura 13,6-0,7=12,9
7 1437m temperatura 12,9-0,7=12,2
8 1537m temperatura 12,2-0,7=11,5
9 1637m temperatura 11,5-0,7=10,8
10 1737m temperatura 10,8-0,7=10,1
11 1837m temperatura 10,1-0,7=9,4
GIEWONT 1900m - temperatura 9,4°C
II sposób rozwiązania zadania (stosowanie wiadomości dotyczących ciągu arytmetycznego)
Analiza zadania
Dane: a1=16,4(temperatura w Zakopanym); r= -0,7 (obniżka temperatury); n=11
Szukane: a11- temperatura na Giewoncie
Obliczenia
a11 = a1+10r
a11 = 16,4 + 10(- 0,7) = 9,4
I sposób rozwiązania zadania 2b
Uczniowie nanoszą dane na wykres
1 Rysy 2503m temperatura 8,7
2 2403m temperatura 8,7+0,7=9,4
3 2303m temperatura 9,4+o,7=10,1
4 2203m temperatura 10,1+0,7=10,8
5 2103m temperatura 10,8+0,7=11,5
6 2003m temperatura 11,5+0,7=12,2
7 1903m temperatura 12,2+0,7=12,9
8 1803m temperatura 12,9+0,7=13,6
9 1703m temperatura 13,6+0,7=14,3
10 1603m temperatura 14,3+0,7=15
11 1503m temperatura 15+0,7=15,7
12 1403m temperatura 15,7+0,7=16,4
MORSKIE OKO 1393m - temperatura 16,4°C
II sposób rozwiązania zadania (stosowanie wiadomości dotyczących ciągu arytmetycznego)
Analiza zadania
Dane: a1=8,7(temperatura na Rysach); r= 0,7 (wzrost temperatury); n=12
Szukane: a12- temperatura nad Morskim Okiem
Obliczenia
a12 = a1+11r
a12 = 8,7 + 11⋅0,7 = 16,4
Załącznik nr3
ZADANIE 3
Składamy 2 stycznia do banku 100zł na oprocentowanie 3% miesięcznie, tzn. ostatniego dnia miesiąca bank dopisuje do kwoty znajdującej się na koncie 3% tej kwoty i kwota ta wchodzi do podstawy oprocentowania w następnym miesiącu. Jaką kwotą będziemy dysponowali po upływie 2 kwartałów nie dokonując wpłat ani wypłat.
I sposób rozwiązania zadania
I miesiąc wpłata 100zł
II miesiąc wpłata 100zł + 3%*100zł =103zł
III miesiąc wpłata 103zł + 3%*103zł =106,09zł
IV miesiąc wpłata 106,09zl +3%*106,09zł = 109,2727 ≅ 109,27zł
V miesiąc wpłata 109,27zl +3%*109,27zł = 112,5508 ≅ 112,55zł
VI miesiąc wpłata 112,55zzł + 3%*112,55zł = 115,9274≅ 115,93zł
II sposób rozwiązania zadania (stosowanie wiadomości dotyczących ciągu geometrycznego)
Analiza zadania
Dane: a1 = 100(pierwsza wpłata); q = 1,03; n = 6 (ilość miesięcy po dwóch kwartałach)
Szukane: a6 (kwota po dwóch kwartałach)
Obliczenia
a6 = a1 ·q5
a6 = 100⋅ (1,03)5 = 115,93
ZADANIE 4 (praca indywidualna)
Rozwiąż zadanie 3 w przypadku oprocentowania 9% kwartalnie.
Załącznik nr4
KARTA PRACY UCZNIA
ZADANIE 1
Składając do kasy oszczędności, w każdym miesiącu o 20zł więcej niż w poprzednim uzbieramy po n miesiącach 1845zł. Oblicz liczbę miesięcy n, jeżeli pierwszy wkład wynosił 125zł.
I sposób rozwiązania zadania
II sposób rozwiązania zadania (stosowanie wiadomości dotyczących ciągu arytmetycznego)
ZADANIE 2
Temperatura w górach obniża się latem o 0,7ºC na każde 100m wzniesienia. Oblicz:
Temperaturę na Giewoncie (1900m), gdy w Zakopanym (837m) jest 16,4ºC.
Temperaturę nad Morskim Okiem (1393m), gdy na Rysach (2503m) jest 8,7ºC.
I sposób rozwiązania zadania 2a
II sposób rozwiązania zadania (stosowanie wiadomości dotyczących ciągu arytmetycznego)
I sposób rozwiązania zadania 2b
II sposób rozwiązania zadania (stosowanie wiadomości dotyczących ciągu arytmetycznego)
ZADANIE 3
Składamy 2 stycznia do banku 100zł na oprocentowanie 3% miesięcznie, tzn. ostatniego dnia miesiąca bank dopisuje do kwoty znajdującej się na koncie 3% tej kwoty i kwota ta wchodzi do podstawy oprocentowania w następnym miesiącu. Jaką kwotą będziemy dysponowali po upływie 2 kwartałów nie dokonując wpłat ani wypłat.
Lekcja pokazowa dla Zespołu Przedmiotowego - przeprowadziła mgr Ewa Szatkowska
Strona 1 z 9
ZAKOPANE
RYSY
ZAKOPANE
RYSY
Wyszukiwarka