Poprawa sprawozdania
Przebieg ćwiczenia
![]()
![]()
Pierwszą rzeczą jaką należało wykonać, aby rozpocząć pracę ze spektrometrem scyntylacyjnym było jego wyskalowanie, czyli przypisanie poszczególnym kanałom konkretnych energii. Do dyspozycji mieliśmy trzy izotopy :
![]()
Jak wynika ze schematów rozpadu najwłaściwszy do wyskalowania jest preparat kobaltowy. Po pierwsze ma największą spośród podanych trzech izotopów energię kwantów oraz, co najważniejsze jądra atomów niklu emitują dwa kwanty γ o różnych wartościach energii(co daje jeden punkt więcej w porównaniu z pozostałymi preparatami do wyznaczenia prostej skalowania).
Zjawisko fotoelektyczne
Cechą charakterystyczną tego zjawiska jest fakt, że kwanty γ znikają w całości przekazując swą energię elektronom na jednej z powłok elektronowych. Tak więc spektrometr rejestrujący widmo energetyczne elektronów da na wyjściu impulsy odpowiadające energii kwantu γ. Z analizy widma energetycznego kwantów preparatu kobaltowego łatwo dostrzec dwa fotopiki o największej energii:
Pik 2 - 1.33 MeV - energia kwantu γ emitowanego przez jądro 60 Ni w stanie o energii
1,33 MeV przy przejściu do stanu o energii 1,33 MV
Pik 4 - 1.17 MeV - energia kwantu γ emitowanego przez jądro 60 Ni w stanie o energii
2,50 MeV przy przejściu do stanu o energii 1,33 MV
Zjawisko Comptona
Polega na rozproszeniu kwantów γ na swobodnych elektronach(elektron nie uzyskuje całej energii kwantu γ). Wskutek komptonowskich zderzeń kwantów γ o energii Eγ powstaje : strumień kwantów γ o energiach Eγ'∈(Eγ; ), a także strumień elektronów o energiach Ee∈(0; ). Strumień kwantów γ może później oddziaływać z atomami scyntylatora. Zjawisko comptonowskiego rozproszenia kwantów γ na swobodnym elektronie można zaobserwować na rysunku 1 od pików 7 do 9. Pik 9 powstaje od kwantów rozproszenia komptonowskiego i jest maksimum rozproszenia wstecznego kwantów, które wywołały w krysztale zjawisko fotoelektryczne. Korzystając ze wzoru na energię elektronów w funkcji kąta rozproszenia Eγmin możemy stwierdzić jaka jest energia tego punktu. Właśnie temu punktowi odpowiada pik 9.
Następnie na podstawie trzech punktów wyznaczamy prostą skalowania:
E=aN+b
,gdzie
E- energia odpowiadająca kwantowi N
N- numer kanału
a=(3962±5)*10-7 [MeV/kanał]
b=(-33.2±1.2)*10-3 [MeV/kanał]
Prosta skalowania jest przedstawiona na rysunku 2. Przy jej pomocy można wyznaczyć energię dowolnych punktów widma energetycznego dla dowolnych nieznanych izotopów. Poniższe tabele przedstawiają wyniki pomiarów punktów składających się na określone widma. Zostały także wyznaczone błędy energii:
ΔE= NΔa + Δb
Dla Co
Nr pkt. |
2 |
4 |
5 |
6 |
7 |
9 |
11 |
E[MeV] |
1.33 |
1.17 |
1.02 |
0.96 |
0.9 |
0.21 |
0.06 |
ΔE*10-3 [MeV] |
2.5 |
2.4 |
2.2 |
2.1 |
2.1 |
1.4 |
1.2 |
Dla Cs
Nr pkt. |
1 |
2 |
3 |
4 |
5 |
6 |
E[MeV] |
0.65 |
0.53 |
0.46 |
0.43 |
0.18 |
0.05 |
ΔE*10-3 [MeV] |
1.2 |
1.2 |
1.2 |
1.2 |
1.2 |
1.1 |
Dla Na
Nr pkt. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
E[MeV] |
1.25 |
1.12 |
1.05 |
0.97 |
0.5 |
0.41 |
0.34 |
0.29 |
0.17 |
0.08 |
ΔE*10-3 [MeV] |
2.4 |
2.3 |
2.2 |
2,2 |
1,7 |
1,6 |
1,5 |
1,4 |
1,3 |
1,3 |
Następnie określiłem zdolność rozdzielczą spektrometru na podstawie poszczególnych widm energetycznych:
R=ΔE/E *100%
Preparat kobaltowy
pik 2 R=6.9 %
pik 4 R=7.2 %
Preparat cezowy
R= 10%
Preparat sodowy
R= 8 %
![]()
Wnioski:
Kobalt
Preparat kobaltowy wskutek zajścia efektu fotoelektrycznego emituje strumienie promieniowania γ o energiach 1,33MeV oraz 1.17 MeV. Pod wpływem wymienionego zjawiska powstają dwa strumienie elektronów o energiach kinetycznych odpowiadających tym energiom oraz strumień promieniowania X. W otrzymanym widmie zjawiskom tym odpowiadają piki 2 i 4.
Strumień promieniowania γ o energii 1.17 MeV wywołuje efekt Comptona. W wyniku tego oddziaływania powstaje strumień elektronów o energiach od 0 do 0,96 Me, a także strumień promieniowania γ o energiach od 0,21 do 1,17 MeV. Punktk 6 odpowiada krawędzi komptonowskiej. Jest maksymalna energia strumienie elektronów powstałych w zjawisku Comptona(Ee=0,96MeV) . Strumień promieniowania γ' o energii 0.21MeV wywołuje efekt fotoelektryczny, w wyniku którego powstaje strumień elektronów o energii 0.21 MeV (pik 9) oraz strumień promieniowania. Promieniowanie X powoduje wystąpienie zjawiska fotoelektrycznego w wyniku którego powstaje strumień elektronów o energii około 0.053MeV (pik 11).
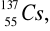
Cez
Preparat cezowy emituje promieniowanie γ o energii 0.66MeV. Pik 1 powstał w wyniku zajścia zjawiska fotoelektrycznego, wywołanego oddziaływaniem kwantów γ. W wyniku tego powstaje strumień elektronów o energii kinetycznej 0.65MeV.
Piki od 3 do 5 powstały w wyniku występowania zjawiska rozpraszania komptonowskiego. W wyniku oddziaływania kwantów γ o energii 0.66MeV powstał strumień elektronów o energii w zakresie od 0 do 0.48 MeV oraz strumień promieniowania γ o energiach od 0.18 do 0.66 MeV. Pik 3 odpowiada maksymalnej energii elektronu (0.48MeV). Wartość doświadczalna wynosi 0.46MeV.
W wyniku oddziaływania promieniowania γ o energii 0.18 powstał pik 5 w wyniku zjawiska fotoelektrycznego. W wyniku tych samych zjawisk powstaje strumień kwantów γ, który z kolei wywołuje kolejne efekty fotoelektryczne. W wyniku tego powstają strumienie elektronów o energii 0.052MeV (pik 6 ).
![]()
Sód
Preparat emituje promieniowanie γ o energii 1.27 MeV. Fotopik o wierzchołku w punkcie 1 powstał w wyniku zjawiska fotoelektrycznego, który został wywołany strumieniem promieniowania γ o energii 1.27MeV. W wyniku tego powstał strumień elektronów o energii 1.27 MeV oraz promieniowanie X.
Ten sam strumień kwantów γ wywołuje zjawisko Comptona. W wyniku tego powstaje strumień elektronów o energiach z zakresu od 0 do 1.06 MeV oraz strumień kwantów γ o energiach z zakresu od 0.22 do 1.27 MeV. Pikowi 3 odpowiada maksymalna energia elektronów (1.06MeV), zmierzona doświadczalnie wynosi ona 1.05MeV. Pik ten stanowi krawędź komptonowską. Pik 5 powstał w wyniku zajścia zjawiska fotoelektrycznego, które zostało wywołane strumieniem kwantów γ o energii 0.5 MeV. Kwanty te powstały w wyniku zajścia zjawiska tworzenia par elektron-pozyton. W wyniku występowania wymienionego zjawiska fotoelektrycznego powstaje strumień elektronów o energiach ok. 0.5MeV oraz strumień promieniowania X. Kwanty gamma o energii 0.5 MeV wywołują zajście zjawiska Comptona. Co powoduje powstanie strumieni elektronów o energii od 0 do 0.33MeV oraz strumieni kwantów γ o energii od 0.17 do 0.5 MeV. Pik 7 reprezentuje krawędź komptonowską. W wyniku oddziaływania kwantów γ o energii 0.17MeV z kierunkiem powstał kolejny pik 9. Pik 11 powstał w wyniku zajścia zjawiska fotoelektrycznego. Wyniku tego powstał strumień elektronów o energii około 0.05MeV.
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka