Przykładowe zadania z matematyki

Zadanie 1.

1. Rozwiązanie:

Aby obliczyć granicę wyciągam wyrażenia o najwyższym stopniu zarówno w liczniku jak i mianowniku:

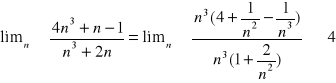
*Objaśnienie:

Biorąc pod uwagę pierwszy nawias (w liczniku): mianowniki w ułamkach dążą do nieskończoności, a więc same ułamki do odwrotności, czyli zera. Opierając się na tym wysnuwamy wniosek, że nawias1 dąży do czwórki. Nawias2 analogicznie dąży do 1. W skrótowym zapisie mamy 4n³/1n³. Skracamy jak zwykły ułamek i wychodzi nam 4.

**Dla szukających w książkach:

Włodzimierz Krysicki, Lech Włodarski: „Analiza matematyczna w zadaniach”, Wyd. XXVIII, Warszawa 2001, „II.Ciągi nieskończone”,str.30-31

Odpowiedź: Granica dąży do 4.

b)

Obliczając daną granicę korzystam z następującego wzoru teorii granic:

jeżeli lim _n→∞ a_n=0 i ciąg jest niezerowy

A dokładniej z jego szczególniejszego wzoru:n

Rozwiązanie:

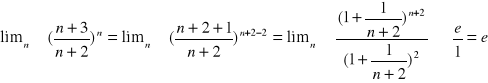
*Objaśnienia:

Najpierw zamieniam ułamek niewłaściwy tak, aby dostosować go do wzoru, a więc n+3 rozpisuję na n+2. Następnie operuję na potęgach, aby dostosować licznik do wzoru (to znaczy, aby mogła powstać w liczniku taka potęga, jak w mianowniku ułamka(po 2 znaku =). Licznik zatem dąży do e, a mianownik do 1 (jak w poprzednim podpunkcie).

Liczba e to oczywiście podstawa logarytmów naturalnych, liczba Eulera, około 2,71828.

**Dla szukających w książkach:

Włodzimierz Krysicki, Lech Włodarski: „Analiza matematyczna w zadaniach”, Wyd. XXVIII, Warszawa 2001, „II.Ciągi nieskończone”,str.34-35

Odpowiedź: Granica dąży do liczby e, stałej Eulera, około 2,71.

c)

Rozwiązanie:

Licząc tą granicę dzielę każdy wyraz przez największą liczbę z wykładnikiem n..

*Objaśnienia:

W ułamku piętrowym, np. ułamek 2ⁿ/5ⁿ dąży do zera, ponieważ

A. 2 do n dążącego do nieskończoności „rośnie” wolniej niż 5 do n dążącego do nieskończoności

B. Skoro 2<5 to obie strony podniesione do tej samej potęgi nie zmieniają znaku równości, a więc 2 do n < 5 do n, co pokazuje nam, że (2 do n/5 do n) < 1, a więc ułamek dąży do zera.

**Dla szukających w książkach:

Włodzimierz Krysicki, Lech Włodarski: „Analiza matematyczna w zadaniach”, Wyd. XXVIII, Warszawa 2001, „II.Ciągi nieskończone”,str.33 (Zadanie 2.7, około połowy strony)

Odpowiedź: Granica dąży do 1.

d)

Korzystam z wzoru algebry elementarnej:

A² - B² = (A - B) * (A+B)

I przekształcam go na wzór z ułamkiem, aby móc pozbyć się pierwiastka:

Rozwiązanie:

Korzystając z przekształconego powyżej wzoru obliczam granicę:

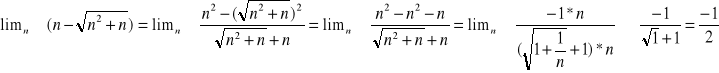
*Objaśnienia:

Po pierwszym znaku „=” podstawiam pod wzór, następnie podnoszę do kwadratu i opuszczam niwelujące się wyrazy n² i - n². Otrzymuję postać, w której wystarczy wyciągnąć najwyższe potęgi przed nawias i zauważyć jeden ułamek dążący do zera.

**Dla szukających w książkach:

Włodzimierz Krysicki, Lech Włodarski: „Analiza matematyczna w zadaniach”, Wyd. XXVIII, Warszawa 2001, „II.Ciągi nieskończone”,str.32 (Zadanie 2.5, około początku strony)

Odpowiedź: Granica dąży do -1/2.

---