Sprawozdanie ćw. 24
Badanie długości fali świetlnej za pomocą siatki dyfrakcyjnej
Bielinski Rafał A-21
Wstęp
Spójna wiązka światła przechodząc przez dwie jednakowe szczeliny ulega na nich ugięciu, dając po przejściu przez szczelinę dwie fale kuliste interferujące ze sobą. W wyniku interferencji otrzymuje się na ekranie umieszczonym w pewnej odległości za szczelinami jasne i ciemne prążki interferencyjne.
Siatka dyfrakcyjna jest powieleniem doświadczenia z dwiema szczelinami. Zasadnicza różnica polega na tym, że zamiast dwóch znajduje się znacznie więcej jednakowych, równoległych szczelin.
W wyniku powiększenia liczby szczelin w widmie dyfrakcyjnym na ekranie po obu stronach środkowego maksimum rzędu zerowego, maksima boczne stają się coraz węższe i jaśniejsze. Jest to związane z tym, że coraz większa liczba promieni bierze udział w interferencji. Zjawisko to nazywa się interferencją wielopromieniową. W takiej sytuacji nie można mówić o zlokalizowanym ciemnym minimum dyfrakcyjnym.
Niech fala świetlna pada na siatkę dyfrakcyjną. Ze środka każdej szczeliny prowadzimy normalną do promienia ugiętego na sąsiedniej szczelinie. Jeżeli d jest odległością między środkami każdej pary dwóch sąsiednich szczelin, - kątem, jaki tworzy kierunek promienia ugiętego z normalną do powierzchni siatki, - różnicą dróg między dwoma ugiętymi sąsiednimi promieniami, to tak jak w przypadku interferencji na dwóch szczelinach
sin = /d.
Fale przechodzące przez szczeliny będą w fazie i będą się wzmacniać wszędzie tam, gdzie
=m,
przy czym m = 0, 1, 2 - rząd widma, - długość fali świetlnej.
Wobec tego położenie maksimów dane jest przez
d sin = m.
Przebieg doświadczenia
Pierwsza część doświadczenia przeprowadzona była z udziałem lampy sodowej. Długość fali świetlnej wynosiła 589,3 nm. Przed przystąpieniem do doświadczenia ustawiliśmy siatkę dyfrakcyjną równolegle do kolimatora, wcześniej ustawiając wartość 0 na noniuszu. Następnie zbadaliśmy odchylenie kątowe prążków I, II i III rzędu. By stwierdzić, że siatka jest dobrze ustawiona różnice pomiędzy prążkami tych samych rzędów nie mogą być większe niż 5'.
|
I rząd |
II rząd |
II rząd |
Lewe prążki |
6º 46' |
13º 32' |
20º 38' |
Prawe prążki |
6º 48' |
13º 38' |
20º 42' |
Wartości średnie |
6º 47' |
13º 35' |
20º 40' |
Wartości w radianach |
0,0376π |
0,075π |
0,112π |
Wyznaczanie stałej siatki dyfrakcyjnej
Pomiar drugiego rzędu nie zgadza się z tym założeniem, ale ponieważ I i III rząd mieszczą się w dopuszczalnych normach, przyjmujemy dane ustawienie jako prawidłowe.
d sin = m
Korzystając z tego wzoru wyliczam wartość „d”, czyli stałą siatki dyfrakcyjnej.
d= m/sin
d1= 1x 589,3 nm/ sin0,0376 π
d1= 4989,23 x 10^-9 [m]
d2= 2x 589,3n/sin0,075 π
d2= 5018,32 x 10^-9 [m]
d3= 3 x 589,3n/sin0,112 π
d3= 5152,53 x 10^-9 [m]
Średnia wartość d
d= (d1+d2+d3)/3= (4989,23 + 5018,32 + 5152,53)/3 = 5053,36 x 10^-9 [m]
Wyznaczanie błędu stałej siatki
Rachunek błędu:
![]()
=> 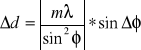
∆d1 = |(1x589,3nm) / sin²0,0376 π | x sin∆ ,x 10^-9 [m]
∆d2 = |(2x589,3nm) / sin²0,075 π | x sin∆ ,x 10^-9 [m]
∆d3 = |(3x589,3nm) / sin²0,112 π | x sin∆ ,x 10^-9 [m]
∆d = (∆d1+∆d2+∆d3)/3
∆d= 15,25 x 10^-9
Stała siatki wynosi, więc 5053,36 x 10^-9 +- 15,25 x 10^-9m
Pomiar kątów ugięcia prążków fal emitowanych przez lampę neonową oraz pomiar długości tej fal i ich błędy
Tabela dla ugięć I rzędu
Kolor |
Kąt ugięcia po lewej stronie |
Kąt ugięcia po prawej stronie |
Średnie ugięcie |
Średnie ugięcie w radianach |
Fiolet |
5° |
5° |
5° |
0,028π |
Zielono-niebieski |
6° 14' |
6° 16' |
6° 15' |
0,035π |
Żółty |
6° 44' |
6° 46' |
6° 45' |
0,036π |
Pomarańczowy |
7° |
7° |
7° |
0,039π |
Czerwony |
7° 20' |
7° 22' |
7° 21' |
0,040π |
Tabela ugięć dla II rzędu
Kolor |
Kąt ugięcia po lewej stronie |
Kąt ugięcia po prawej stronie |
Średnie ugięcie |
Średnie ugięcie w radianach |
Zielony |
12° 36' |
12° 34' |
12° 35' |
0,07π |
Żółty |
13° 32' |
13° 32' |
13° 32' |
0,075π |
d sin = m
= d sin /m
I rząd
λfiolet = 5053, 36 x 10^-9 x sin 0,028 π/1= 440,43 nm
λzielono-niebieski = 5053, 36 x 10^-9 x sin 0,035 π/1= 550,14 nm
λżółty = 5053, 36 x 10^-9 x sin 0,036 π/1= 593,96 nm
λpomarańcz = 5053, 36 x 10^-9 x sin 0,039 π/1= 615,85 nm
λczerwony = 5053, 36 x 10^-9 x sin 0,04 π/1= 646,48 nm
λfiolet = 5053, 36 x 10^-9 x sin 0,028 π/1= 440,43 nm
λfiolet = 5053, 36 x 10^-9 x sin 0,028 π/1= 440,43 nm
II rząd
λzielony = 5053, 36 x 10^-9 x sin 0,07 π/2= 550,46 nm
λżółty = 5053, 36 x 10^-9 x sin 0,075 π/2= 591,27 nm
6. Rachunek błędów
![]()
Rząd I
∆λfiolet = |sin 0,028 π/1|x 15,25 x 10^-9 + |5053,36 x10^-9/1| x sin∆0,00002 π = 7,88 x 10^-11 m
∆λzielono-niebieski = |sin 0,035 π/1|x 15,25 x 10^-9 + |5053,36 x10^-9/1| x sin∆0,00002 π = 8,47 x 10^-11 m
∆λżółty= |sin 0,036 π/1|x 15,25 x 10^-9 + |5053,36 x10^-9/1| x sin∆0,00002 π = 8,55 x 10^-11 m
∆λpomarańcz = |sin 0,039 π/1|x 15,25 x 10^-9 + |5053,36 x10^-9/1| x sin∆0,00002 π = 8,80 x 10^-11 m
∆λczerwony = |sin 0,04 π/1|x 15,25 x 10^-9 + |5053,36 x10^-9/1| x sin∆0,00002 π = 8,87 x 10^-11 m
Rząd II
∆λzielony = |sin 0,07 π/2|x 15,25 x 10^-9 + |5053,36 x10^-9/2| x sin∆0,00002 π = 5,7x 10^-11 m
∆λżółty = |sin 0,075 π/2|x 15,25 x 10^-9 + |5053,36 x10^-9/2| x sin∆0,00002 π = 5,91 x 10^-11 m
Wyniki końcowe
λfiolet = 5053, 36 x 10^-9 x sin 0,028 π/1= 440,43 nm +- 7,88 x 10^-11 m
λzielono-niebieski = 5053, 36 x 10^-9 x sin 0,035 π/1= 550,14 nm +- 8,47 x 10^-11 m
λżółty = 5053, 36 x 10^-9 x sin 0,036 π/1= 593,96 nm +- 8,55 x 10^-11 m
λpomarańcz = 5053, 36 x 10^-9 x sin 0,039 π/1= 615,85 nm +- 8,80 x 10^-11 m
λczerwony = 5053, 36 x 10^-9 x sin 0,04 π/1= 646,48 nm +- 8,87 x 10^-11 m
II rząd
λzielony = 5053, 36 x 10^-9 x sin 0,07 π/2= 550,46 nm +- 5,7x 10^-11 m
λżółty = 5053, 36 x 10^-9 x sin 0,075 π/2= 591,27 nm +- 5,91 x 10^-11 m
Wartości tablicowe:
Fiolet : 433, 4 x 10^-9 [m]
Zielono Niebieski: 488,5 x 10^-9 [m]
Żółty: 582,2 x 10^-9 [m]
Pomarańcz: 603 x 10^-9 [m]
Czerwony 640 x 10^-9 [m]
Zielony: 537,5 x 10^-9 [m]
Wnioski
Dzięki temu doświadczeniu można było zaobserwować zjawisko rozszczepienia światła, a także zobaczyć działanie siatki dyfrakcyjnej. Wartości tablicowe potwierdzają większość pomiarów, co oznacza, że doświadczenie zostało wykonane prawie bezbłędnie. Jedynie wartość Zielono-Niebieska znacznie odbiega od wartości tablicowej, jednak jej wartość nie odbiega od wartości światła widzialnego.
Wyszukiwarka