Zadania z geometrii
Napisać równanie płaszczyzny przechodzącej przez punkt P (1, 2, 3), która jest równoległa do prostych
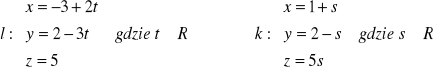
Wyznaczyć sinus lub kosinus kąta między prostymi
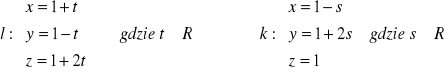

Dany jest punkt P (1, 1, 1) i płaszczyzna π: x + 2y - z + 3 = 0. Znaleźć rzut prostokątny punktu P na płaszczyznę π.
Napisać równanie parametryczne płaszczyzny przechodzącej przez punkt P (4, 7, 2) i prostopadłej do prostej

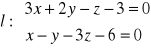
Napisać równanie parametryczne prostej przechodzącej przez punkt P (1, 2, 3) i równoległej do prostej
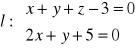
Znaleźć punkt symetryczny do punktu A (6, -3, 0) względem płaszczyzny π: x + y + z = 0.
Punkty A (2, 3, 2) i B (0, 1, 1) są kolejnymi wierzchołkami rombu ABCD, zaś wektor
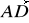
jest zgodnie równoległy do wektora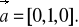
Obliczyć pole tego rombu.Obliczyć kąt między prostymi
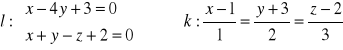
Dany jest punkt P (1, 1, 1) i prosta
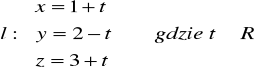
Znaleźć rzut prostokątny punktu P na prostą l.Napisać równanie płaszczyzny równoległej do osi Oz i przechodzącej przez punkty P (2, 3, -1), Q (-1, 2, 4).
Napisać równanie parametryczne i kierunkowe prostej przechodzącej przez punkt P (3, 2, -5) i prostopadłej do płaszczyzny
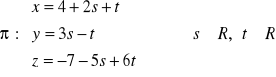
Obliczyć pole trójkąta, którego wierzchołkami są punkty przecięcia osi układu współrzędnych
z płaszczyzną π: 2x + y + 3z = 6Obliczyć odległość punktu P (2, 3, -1) od prostej
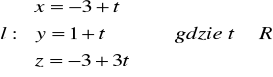
.Obliczyć pole trójkąta utworzonego na płaszczyźnie x + y + z = 10 w wyniku jej przecięcia płaszczyznami x = 1, y = 2 oraz z = 3.
Wyznaczyć równanie płaszczyzny przechodzącej przez punkt P = (1, -1, 2) i prostą
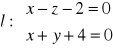
Napisać równanie płaszczyzny rozpiętej na przecinających się prostych
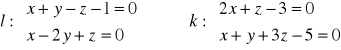
Wyszukiwarka