1. Zaprojektować izotermiczny reaktor okresowy oraz izotermiczny reaktor zbiornikowy przepływowy dla reakcji I- rzędowej:

C₂H₄O+H₂o→HO-CH₂-CH₂-OH

Wydajność produkcyjna reaktora ma wynosić L_p=900[kg] glikolu etylenowego na godzinę (dla reaktora okresowego nie uwzględniać okresów załadunku i rozładunku). Stopień przemiany α_A=0,6 (A - tlenek etylenu, B - woda, C - glikol etylenowy). Gęstość mieszaniny należy przyjąć jako stałą, wynoszącą 1000[kg/m³]. Woda doprowadzana jest z trzykrotnym nadmiarem. Stała szybkości reakcji k=9,81∙10^-4[s^-1].

a) reaktor okresowy

woda doprowadzana z trzykrotnym nadmiarem

b) reaktor zbiornikowy przepływowy

Reaktor zbiornikowy z idealnym mieszaniem:

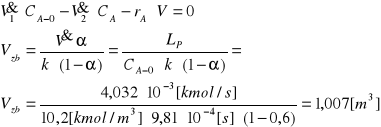
2. Proces otrzymywania glikolu etylenowego, opisany w poprzednim zadaniu, prowadzono w identycznych warunkach, z tym że zamiast pojedynczego reaktora zbiornikowego zastosowano kaskadę 3 reaktorów o tej samej sumarycznej objętości. Porównać stopnie przemiany i wydajność dla przypadku, gdyby zastosowano aparaty o objętościach 0,2 0,3 0,507[m³] oraz dla przypadku, w którym stopnie kaskady miały by równe pojemności.

3. Należy wyprodukować 50000[kg/dobę] octanu etylu z alkoholu etylowego i kwasu octowego, przy czym reakcję opisuje następujące równanie:

C₂H₅OH+CH₃COOH=CH₃COOC₂H₅+H₂O

Szybkość reakcji w fazie ciekłej określona jest równaniem:

R_B=k[C_AC_B-C_pC_Q/K_C]

Gdzie A - C₂H₅OH_, B - CH₃COOH, P - CH₃COOC₂H₅, Q - H₂O.

Znaleziono eksperymentalnie k=7,93∙10^-6[m³/kmol∙s], a stała równowagi K_C=2,93.

Skład surowca jest następujący:

x_0A=0,46[kgA/kg miesz] ; x_0B=0,23[kgB/kg miesz] ; x_0Q=0,31[kgQ/kg miesz].

Reakcję należy prowadzić do α_B=0,35. przyjąć stałą gęstość wynoszącą ρ=1020[kg/m³]. Obliczyć wielkość reaktora zbiornikowego przepływowego, który jest niezbędny do zapewnienia żądanej produkcji.

4. Do reaktora z idealnym mieszaniem dopływa 10^-4[m³/s] surówki zawierającej składnik A.Stężenie składnika A w surówce wynosi 1,44[kmol/m³]. W reaktorze zachodzi reakcja według równania stechiometrycznego: A→B+C. Z przeprowadzonych doświadczeń wynika, że równanie kinetyczne tej reakcji należy zapisać następującym wzorem r=k∙c^0,5. Stała szybkości reakcji wynosi 1,28∙10^-4[s^-1kmol^0,5m^-1,5]. Znaleźć objętość reaktora zapewniającą uzyskanie konwersji równej 0,64.

5. Reakcję odwracalną A+B=R+S, zachodzącą w fazie ciekłej, należy przeprowadzić w ciągłym reaktorze zbiornikowym o pojemności 120[dm³]. Stałe szybkości reakcji wynoszą k₁=7[dm³/mol∙min] k₂=3[dm³/mol∙min]. Reaktor jest zasilany dwoma strumieniami o koncentracjach: C_0A=2,8[mol/dm³] i C_0B=1,6[mol/dm³], przy czym objętościowe natężenia przepływu obu strumieni są identyczne. Jakie powinny być natężenia przepływu, jeśli żądana jest 75%konwersja składnika B? Gęstość mieszaniny reagującej może być uważana za niezmienną.

6. Zaprojektować okresowy reaktor izotermiczny, w którym przebiega r-cja I-rzędowa: A→B, do wyprodukowania 100[kgB/h], gdzie M_B=80[kg/kmol], stała szybkość reakcji k=0,1[s^-1], stopień przereagowania składnika A wynosi 0,99, stężenie początkowe składnika A C_A0=0,2[kmol/m³]. Założyć stała gęstość. Znaleźć objętość reakcyjną.

7. Dla pewnej reakcji I-rzędu można dobrać reaktor zbiornikowy z idealnym wymieszaniem lub rurowy z przepływem tłokowym. Jaki będzie stosunek objętości reaktora zbiornikowego do rurowego , jeżeli reakcja jest nieodwracalna, a stopień przemiany wynosi 0,8? Założyć stałą gęstość i takie same objętościowe natężenia przepływu w obu reaktorach.

8. Reakcję estryfikacji ftalanu ortylowego alkoholem ortylowym prowadzi się w izotermicznym reaktorze zbiornikowym przepływowym w temp. 170°C w obecności tytanianu butylowego jako katalizatora homogenicznego. Reakcja zachodzi w fazie ciekłej według równania :

F + A → FO + W

Ftalan jednooktylowy alkohol oktylowy ftalan oktylowy woda

Reakcja jest praktyczne nieodwracalna ze względu na natychmiastowe wyprowadzenie wody ze środowiska reakcji. Jest to reakcja II-rzędu, r_F = k c_F c_A. Stała szybkość k=0,02[m³/kmol min]przy stosowanym stężeniu katalizatora C_K=0,0096[mol/dm³]. Przyjąć , że gęstość mieszaniny reakcyjnej jest stała i wynosi Q_m=0,849[kg/m³].alkochol ortylowy jest użyty w nadmiarze przy czym:

1). Określić zastępczy czas przebywania (średni czas przebywania) niezbędny dla osiągnięcia stopnia przemiany ftalany jednooktylowego α_F=0,99.

2). Wyznaczyć objętość przestrzeni reakcyjnej przy założonej zdolności produkcyjnej L_p=7500∙10³[kg/rok] ftalany ortylowego i dla stopnia przemiany α_F=0,99.

---