Wstęp teoretyczny do ćwiczeń laboratoryjnych numer 76:

Wyznaczanie współczynnika załamania szkła za pomocą spektrometru

Celem tego ćwiczenia jest wykonanie pomiarów kąta łamiącego i kąta minimalnego odchylenia pryzmatu. Będziemy mieli również za zadanie wyznaczyć współczynnik załamania światła dla szkła w funkcji długości fali. Również zajmiemy się wyznaczaniem dyspersji szkła.

Aby otrzymać widmo będziemy posługiwać się spektrometrem. Na pryzmat skierujemy wiązkę światła, a następnie obserwujemy ją przez lunetę. Po odpowiednim ustawieniu lunety otrzymamy punkt przecięcia krzyża w środku wybranego prążka widma. Po czym odczytujemy kąt obrotu lunety na kole podziałowym.

Prawo Snelliusa

Światło załamuje się na granicy dwóch różnych ośrodków. Właśnie to zjawisko załamania ilościowo opisuje prawo Snelliusa, które możemy wyrazić przez poniższe wzory:

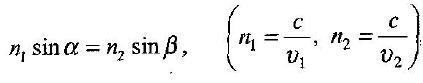
Oznaczenia n₁ i n₂ to bezwzględne współczynniki załamania światła (odpowiednich ośrodków jednego i drugiego); V₁ i V₂ są prędkościami w danym ośrodku; c jest prędkością światła w próżni; natomiast α i β to kąty oznaczające padanie i załamanie promienia świetlnego w danym ośrodku.

Kąt γ

Dwie płaszczyzny optycznie czynne znajdujące się w pryzmacie mogą tworzyć ze sobą kąt γ, który nazywamy kątem łamiącym pryzmatu. Dzieje się tak, jeśli światło monochromatyczne pada na pierwszą płaszczyznę pryzmatu pod kątem α, a następnie załamuje się pod kątem β. Zaraz jednak pada na drugą powierzchnię i ponownie załamuje się pod kątem α. Jednak w tym wypadku musi być spełniona reguła, że kąt padania β musi być mniejszy od kąta granicznego. Ostatecznie światło które przeszło przez pryzmat odchyliło się o kąt γ. Natomiast kąt graniczny jest to maksymalny kąt, pod jakim promienie światła mogą padać, a następnie się załamać. Powyżej wartości tego kąta wiązki światła nie załamią się.

Rozszczepianie światłą w pryzmacie

Jeżeli na powierzchni dwóch płaszczyzn skierujemy wiązkę światła na ich powierzchnię graniczną, pod odpowiednim kątem będącym w przedziale większym od zera, ale mniejszym od kąta granicznego, to wówczas fale o różnych długościach przechodzące do drugiego ośrodka zostaną załamane pod różnymi kątami. Właśnie to zjawisko nosi nazwę rozszczepieniem światła bądź dyspersją.

Pryzmat wykorzystuje się do rozłożenia światła białego na pozostałe barwy. Największe odchylenie posiada kolor fioletowy, zaś najmniejsze pomarańczowy.

Dyspersja średnia

Dyspersja to zależność współczynnika załamania ośrodka od częstotliwości fali świetlnej. Żeby określić wielkość dyspersji w zakresie światła widzialnego stosujemy wzór na dyspersję średnią:

nF jest współczynnikiem załamania dla światła niebieskiego (tzw. linia Fraunhofera F wynosząca 486,1 nm), natomiast nC to współczynnika załamania dla światła czerwonego (tzw. linia Fraunhofera C wynosząca 656,3 nm).

Liczba Abbego

Jest to jedna z liczb prawdopodobieństwa i charakteryzuje stosunek załamania się fali do dyspersji płaszczyzny:

W tym wzorze nD, nF, nC są to współczynniki załamania płaszczyzny dla poszczególnych linii Fraunhofera; V to prędkość.

---