Akademia Górniczo-Hutnicza
w Krakowie
Wydział Górnictwa i Geoinżynierii
Inżynieria Środowiska II
Laboratorium z Mechaniki Płynów
Adam Chwałek
Tomasz Ziomek
Tomasz Szramik
Piotr Kasprzyk
Grupa 2/2, rok II, zespół IV
Data wykonania ćwiczenia: 17.03.2010 rok
Temat: „Pomiar współczynnika lepkości powietrza.
Cel: Wyznaczenie współczynnika lepkości powietrza.
Przebieg ćwiczenia: W celu wyznaczenia współczynnika lepkości należy zmierzyć czas przepływu określonej ilości wody z aspiratora i zarazem objętość przepływającego powietrza przez rurkę kapilarną, oraz odczytać wartość, którą wskazuje manometr. Objętość wypływającej wody mierzymy menzurką, a czas stoperem.
Wstęp teoretyczny:
Lepkość jest właściwością materii we wszystkich stanach skupienia, związaną z oddziaływaniami międzycząsteczkowymi. Lepkością albo tarciem wewnętrznym nazywa się opór, jaki występuje podczas ruchu jednych części (warstw) ośrodka względem innych. W przypadku laminarnego przepływu cieczy w rurce o promieniu R wszystkie jej warstwy poruszają się w kierunkach równoległych, przy czym każda warstwa oddalona o r od osi rurki ma inną prędkość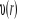 
. Największą prędkość ma warstwa cieczy poruszająca się wzdłuż osi rurki (r=0), a w miarę zbliżania się do ścian rurki prędkość ruchu warstw cieczy maleje, aby na jej brzegu osiągnąć wartość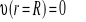 
. Gradient prędkości dυ/dr odpowiada zmianie prędkości cieczy dυ pomiędzy warstwami oddalonymi o nieskończenie małą odległość dr.
Zgodnie z prawem Newtona, siła styczna F potrzebna do nadania cieczy o współczynniku lepkości η gradientu prędkości dυ/dr na powierzchni A równoległej do kierunku przepływu wynosi:
Jednostką współczynnika lepkości dynamicznej zwanego lepkością bezwzględną η w układzie SI jest Nsm-2 = kgm-1s-1. W układzie CGS jednostką lepkości jest puaz, P=gcm-1s-1; 1 P = 10-1 Nsm-2.
Znane są liczne metody wyznaczania lepkości cieczy. Do najczęściej stosowanych należą: metody oparte na pomiarze szybkości przepływu cieczy przez rurkę kapilarną oraz metody oparte na pomiarze szybkości opadania kulki w badanej cieczy.
Działanie wiskozymetrów kapilarnych opiera się na równaniu Hagen'a - Poiseuille'a, zgodnie z którym objętość cieczy V przepływająca w czasie t przez kapilarę o średnicy D i długości l pod wpływem różnicy ciśnień Δp wynosi:
Zakłada się przy tym, że
- badana ciecz jest nieściśliwa
- przepływ jest laminarny
- warstwa poruszająca się w osi kapilary ma prędkość największą, prędkość pozostałych warstw kapilary zmienia się malejąco do zera (dla warstwy przylegającej bezpośrednio do ścianki)
poszczególne warstwy poruszają się ruchem jednostajnym
przepływ cieczy następuje na skutek istnienia różnicy ciśnień na obu końcach kapilary.
Liczba Reynolds'a określa w sposób jednoznaczny charakter przepływu wiążąc ze sobą wielkości gęstości, lepkości, prędkości przepływu i rozmiaru rury. Liczbę Reynoldsa można opisać jako stosunek sił bezwładności do sił tarcia przepływającego medium. Dowolny stan przepływu czynnika jest zawsze jednoznacznie określony przez tę liczbę. Mała jej wartość oznacza przewagę sił lepkości nad siłami bezwładności, duża zaś przewagę sił bezwładności. Należy przyjmować, że dla Re<2300 mamy do czynienia
z przepływem laminarnym a dla Re>3000 z przepływem turbulentnym (burzliwym).
Schemat stanowiska
Aspirator
Szklana rurka
Manometr
5. Wzory użyte do obliczeń:
Wzór Hagen'a-Poisseuilla:
gdzie:
Δp- różnica ciśnień między końcami kapilary
D, L- średnica i długość kapilary
μ- dynamiczny współczynnik lepkości powietrza
Wzór na dynamiczny współczynnik lepkości:
gdzie:
V- objętość wypływającej cieczy
t- czas przepływu cieczy
reszta jak wyżej
Liczba Reynolds'a:
gdzie:
νśr- prędkość średnia powietrza
υ- kinematyczny współczynnik lepkości
reszta jak wyżej
Prędkość średnia powietrza:
gdzie: oznaczenia jak wyżej
Średnia arytmetyczna współczynnika lepkości:
gdzie:
n - liczba pomiarów
Odchylenie standardowe:
Przedział ufności dla wartości średniej:
6. Stałe przyjęte w sprawozdaniu:
ρpow. = 1,168 kg/m3
π = 3,14159
D = 0,0031 m
L = 1 m
tα = 2,262157158
υ = 1,6 x 10 -5 m2/s
wartość tablicowa: μtab = 1,71×10-5
7. Tabela zbiorcza:
|
Δp [Pa] |
t [s] |
V [m3] |
vśr [m/s] |
Re |
μ [Pa∙s] |
1 |
242 |
7,0 |
210∙10-6 |
3,976749 |
770,50 |
1,828∙10-5 |
2 |
235 |
7,4 |
205∙10-6 |
3,672223 |
711,49 |
1,922∙10-5 |
3 |
232 |
7,4 |
210∙10-6 |
3,76179 |
728,85 |
1,852∙10-5 |
4 |
228 |
7,4 |
205∙10-6 |
3,672223 |
711,49 |
1,865∙10-5 |
5 |
223 |
7,4 |
200∙10-6 |
3,582657 |
694,14 |
1,869∙10-5 |
6 |
218 |
7,3 |
198∙10-6 |
3,595417 |
696,61 |
1,821∙10-5 |
7 |
214 |
7,5 |
195∙10-6 |
3,446516 |
667,76 |
1,865∙10-5 |
8 |
210 |
7,4 |
205∙10-6 |
3,672223 |
711,49 |
1,717∙10-5 |
9 |
206 |
7,5 |
195∙10-6 |
3,446516 |
667,76 |
1,795∙10-5 |
10 |
200 |
7,6 |
185∙10-6 |
3,226748 |
625,18 |
1,861∙10-5 |
µ średnie [Pa∙s] |
1,81 x 10-5 |
|||||
odchylenie standardowe [Pa∙s] |
2,1 x 10-7 |
|||||
przedział ufności |
1,795x10-5<1,81x10-5<1,825x10-5 |
|||||
8. Wnioski:
Dla poziomu ufności - częstości 95% . Liczba wyników współczynnika μ znajdujących się poza przedziałem wynosi 4 (40% wyników).
Porównując wyniki obliczeniowe z wartościami tablicowymi, widzimy, że nie różnią się one bardzo między sobą, dlatego możemy przypuszczać że ćwiczenie zostało wykonane
w miarę poprawnie. Nasza liczba Reynoldsa wskazuje na laminarny przepływ płynu co świadczy o tym że ćwiczenie przebiegało bez zakłóceń.
Wyszukiwarka