Uniwersytet Śląski Wydział Techniki Sosnowiec	Sprawozdanie z zajęć laboratoryjnych	Wychowanie Techniczne	Semestr III	Sprawdził
					9.12.2001
		Instytut Problemów Techniki
							Kozielski Piotr Barcik Tomasz		Ocena
			Wyznaczanie współczynnika załamania światła przy pomocy mikroskopu
Zakład

Zagadnienia teoretyczne .

1. CIECZ IDEALNA - CIECZ RZECZYWISTA .

Ciecz idealna pozostająca w spoczynku jest całkowicie nieściśliwa , a będąc w ruchu spełnia dodatkowo warunek braku lepkości . W przyrodzie nie występuje . Rzeczywiste ciecze występujące w przyrodzie odznaczają się niewielką ściśliwością . Prawo Hooke'a w odniesieniu do cieczy zapisujemy :

,

gdzie
nazywamy współczynnikiem ściśliwości cieczy (
dla cieczy doskonałej) . Wskazuje on o jaką część objętości początkowej zmieniła się objętość danej cieczy podczas zmiany ciśnienia o jednostkę .

2. RÓWNANIE CIĄGŁOŚCI , RÓWNANIE BERNOULLIEGO .

Prędkość cząstek wewnątrz płynu może mieć różne wartości w różnych punktach , chociaż w dowolnym punkcie jest ona równoległa do strugi . Niech prędkość tych cząstek w punkcie P wynosi
, a prędkość cząstek w punkcie Q-
. Niech
i
będą odpowiednio przekrojami strugi w P i Q , prostopadłymi do linii prądu w tych punktach . W czasie
element płynu przepływa w przybliżeniu odległość
. Masa płynu
przenikająca
w przedziale czasu
wynosi w przybliżeniu :

czyli strumień masy
równa się w przybliżeniu
. Na to , żeby w tym przedziale czasu ani
, ani A nie zmieniały się w sposób zauważalny na drodze , po której porusza się płyn , musimy wziąć
dostatecznie małe . W granicy , gdy
, otrzymujemy dokładne definicje :

strumienia masy w P :

oraz

strumienia masy w Q :
,

gdzie
i
są, odpowiednio , gęstościami płynu w punktach P i Q . W szczególności strumień masy w punkcie P musi być równy strumieniowi w punkcie Q :

,

albo inaczej

wynik ten wyraża prawo zachowania masy w dynamice płynów .Jeżeli płyn jest nieściśliwy , to równanie przyjmuje prostszą postać :

lub

iloczyn
określa wielkość zwaną często strumieniem objętościowym lub też natężeniem przepływu . Z równania powyższego wynika , że prędkość płynu dla nieściśliwego przepływu ustalonego zmienia się odwrotnie proporcjonalnie do pola powierzchni przekroju i jest większa w węższych częściach strugi . Prawo Bernoulliego . Dotyczy stacjonarnego przepływu nieściśliwej cieczy idealnej . Przepływ stacjonarny to taki , w którym nie ma zawirowań a prędkość cieczy w dowolnie ustalonym punkcie jest stała . W każdym punkcie linii prądu wektor prędkości cieczy jest do niej styczny . Przyjmując powyższe założenia prawo Bernoulliniego dla stacjonarnego przepływu nieściśliwej cieczy idealnej stwierdza , że wzdłuż linii prądu spełniony jest związek :

p+1/2ρv² +ρgh = const.

gdzie p jest ciśnieniem w danym punkcie cieczy , v prędkością przepływu w tym punkcie , ρ gęstością h wysokością względem wybranego poziomu natomiast g oznacza przyspieszenie ziemskie .

3. TARCIE WEWNĘTRZNE CIECZY .

Tarcie wewnętrzne zwane lepkością jest siłą , która przeciwstawia się ruchowi . Ciecz przepływająca przez przewody przylega do ścian przewodu tworząc nieruchomą warstwę . W miarę przesuwania się od ścian przewodu do środka prędkości rośnie . W czasie przepływu cieczy mamy do czynienia z przesuwaniem się jednych warstw względem drugich czemu towarzyszy opór . Właściwości różnych cieczy z punktu widzenia ich lepkości charakteryzuje wielkość zwana współczynnikiem lepkości .

4. WSPÓŁCZYNNIK LEPKOŚCI CIECZY .

Ciecz przepływająca przez przewody przylega do ścian przewodu tworząc nieruchomą warstwę , cylinder z cieczy wewnątrz , którego odbywa się ruch reszty cieczy . W miarę przesuwania się od ścian przewodu do środka prędkość rośnie .

Jeżeli wyodrębnimy dwie warstwy cieczy o powierzchniach S , odległe od siebie o
poruszające się z prędkościami
i
ta siła działająca na górną warstwę i styczna do niej wyraża się wzorem :

,

gdzie
jest dynamicznym współczynnikiem lepkości , a
różnica prędkości obu warstw . Siła lepkości działająca na każde z warstw cieczy jest równa co do wartości sile F. , lecz przeciwnie skierowana . Kierunek jej jest przeciwny do kierunku prędkości względnej danej warstwy .
wyraża siłę lepkości powstająca przy ruchu względnym dwóch warstw z jednostkowej powierzchni jeśli różnica prędkości między warstwami wynosi
, a odległość
.

5. RUCH LAMINARNY , RUCH BURZLIWY , LICZBA REYNOLDSA .

Ruch laminarny występuje gdy wszystkie cząstki płynu poruszają się po torach równoległych do siebie .

Ruch burzliwy występuje , gdy cząstki wykonują ruchy nieuporządkowane , poruszają się w różnych kierunkach . Towarzyszy temu powstawanie nieregularnych linii prądu i wirów.

Liczba Reynoldsa jest związana z gęstością
, współczynnikiem lepkości
, prędkością V oraz średnicą przewodu d :

,

dla Re<2300 występuje laminarny przepływ cieczy , a dla Re>3000 przepływ burzliwy . Przy jej pomocy można wyznaczyć prędkość krytyczną przepływu płynu po której ruch staje się burzliwy.

6. PRZEPŁYW LAMINARNY PRZEZ RURĘ - WZÓR POISEUILLE'A .

W takich warunkach wszystkie cząsteczki poruszają się w kierunkach równoległych do

osi rurki z prędkościami malejącymi wraz z odległością do osi . w płynie można wyróżnić cylindryczne warstwy o stałej prędkości . W idealnym przepływie laminarnym nie zachodzi wymiana cząsteczek przez ścianki tak pomyślanych walców . W rzeczywistości istnieje pewna wymiana cząsteczek , spowodowana ich ruchem cieplnym . Ta wymiana cząsteczek jest czynnikiem działającym na rzecz wyrównania prędkości warstw cylindrycznych , przyspieszającym warstwy wolniejsze a spowalniającym szybsze , leżące bliżej osi .Wzór Poiseuille'a :

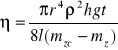
gdzie:

r - promień wewnętrzny kapilary - 0,5035 mm

l - długość kapilary - 196,5 mm

ρ - gęstość cieczy - 0,998 * 10³ kg/m³

h - wysokość słupa cieczy - 100 mm

t - czas wypływu cieczy - 1200 s

m_zc - masa zlewki z cieczą - 60 g

m_z - masa zlewki - 56 g

g - przyspieszenie ziemskie - 9,81 m/s²

Wykonanie ćwiczenia i opracowanie wyników .

• Wartość tablicowa gęstości wody / ρ / w temperaturze / t₀ = 20⁰C / :

ρ = 0,9982*10³ [kg*m^-3]

• Mierzymy / h , l / przy pomocy suwmiarki oraz odpisujemy wartość promienia wewnętrznego kapilary z instrukcji przy ćwiczeniu :

h = 0,21 [m] Δh = 0,002 [m]

l = 0,1965 [m] Δl = 0,00005 [m]

r = 0,001007 [m] Δr = 0,000001 [m]

• Podstawiamy pustą zlewkę pod wylot rurki kapilarnej ; otwieramy kran [K] i włączamy jednocześnie stoper . Po upływie 20 min [1200 s] zamykamy kran wyłączając jednocześnie stoper :

początkowa wysokość słupa wody h1 [m]	końcowa wysokość słupa wody h2 [m]	czas wypływu τ [s]	ilość wody wypuszczonej mzc - mz [g]
0,10	0,07	1200	60 - 56 = 4
Δ = 0,001	Δ = 0,001	Δ = 0,2

Podstawiając zebrane dane do wzoru Poiseuille'a :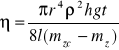


gdzie:

r - promień wewnętrzny kapilary - 0,5035 mm

l - długość kapilary - 196,5 mm

ρ - gęstość cieczy - 0,998 * 10³ kg/m³

h - wysokość słupa cieczy - 100 mm

t - czas wypływu cieczy - 1200 s

m_zc - masa zlewki z cieczą - 60 g

m_z - masa zlewki - 56 g

g - przyspieszenie ziemskie - 9,81 m/s²

Po podstawieniu powyższych danych do wzoru otrzymujemy:


= 4,88439707 * 10 ^-3 kg/m³ ?????????

Obliczamy błąd metodą różniczki zupełnej





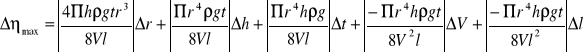
= 0,014917

Dyskusja błędu

Otrzymane wyniki niestety bardzo różnią się od tablicowych, ponieważ według instrukcji ćwiczenia w naczyniu z rurką włoskowatą powinna znajdować się woda destylowana a wartość tablicowa współczynnika lepkości wody w temperaturze 298K wynosi
.

Różnica pomiędzy wartością tablicową, a wyliczoną nie mieści się w granicach błędu pomiaru. Zastosowana metoda pomiaru nie pozwoliła nam na otrzymanie wyniku z dużą dokładnością. Na niedokładność pomiaru mogły mieć wpływ następujące czynniki:

1. błąd pomiaru wysokości słupa cieczy h (podczas ubywania cieczy na końcu wylotu rurki w butli tworzył się bąbelek powietrza co było przyczyną niestałej różnicy ciśnień na końcach rurki kapilarnej).

2. błąd pomiaru długości rurki kapilarnej.

3. błąd pomiaru czasu.

4. błąd pomiaru masy.

Dokładność pomiaru można by zwiększyć, używając większej ilości wody w butli, dłuższej rurki kapilarnej i wydłużając czas trwania doświadczenia. Ponadto na błąd wpłynął fakt, początkowych trudności z udrożnieniem rurki włoskowatej, kilkakrotne próby przeczyszczenia jej nie dawały pożądanego efektu, do tego mieliśmy trudności z pozbyciem się pęcherzyków powietrza w obrębie kranika zwalniającego przepływ wody w skutek czego w czasie przewidzianym na zrobienie ćwiczenia udało nam się tylko wykonać je tylko raz.

1




---