Jan Kędzierski Grzegorz Karczewski Andrzej Serafin	Prowadzący: mgr Justyna Trzmiel	Laboratorium: Fizyka H1 Ćwiczenie: 89
			grupa: poniedziałek 14^15	Pomiar wymuszonej aktywności optycznej.
					Ocena:
data: 22.03.2004

1.Cel ćwiczenia

Zapoznanie się ze zjawiskiem Faradaya, czyli powstawanie dwójłomności kołowej, pomiar stałej Verdeta oraz wyznaczenie wartości ładunku właściwego elektronu e/m.

2. Wprowadzenie teoretyczne.

Ośrodki anizotropowe z dwójłomnością kołową nazywa się inaczej ośrodkami optycznie aktywnymi. W naszym przypadku kołowo dwójłomne były ciała izotropowe w polu magnetycznym. Najlepiej zjawisko to omówić na rysunku

Kierunek propagacji fal jest prostopadły do rysunku powyżej. E(0) oznacza wektor natężenia pola elektrycznego fali wchodzącej, leżący na powierzchni wejściowej (z = 0) ośrodka optycznie aktywnego. Daje on początek dwóm przeciwskrętnym falom E_f(0) i E_s(0) spolaryzowanym kołowo i przechodzącym przez ten ośrodek z różnymi prędkościami. Ta różnica prędkości sprawia, że na powierzchni wyjściowej (z = d) oba wektory E_d (d) i E_s(d) nie są już symetryczne wzglądem E(0), ale tworzą z osiami x i y odpowiednio kąty γ_f i γ_f.

Na powierzchni wyjściowej ośrodka optycznie aktywnego obie fale spola­ryzowane kołowo nakładają się na siebie i tworzą wektor E(d) fali wychodzą­cej. Można wykazać, że fala wychodząca z ośrodka aktywnego optycznie ma taką samą eliptyczność i skrętność jak fala wchodząca do ośrodka, ale azy­muty tych fal różnią się o kąt Γ. Określenie to jest o tyle mylące, że w trakcie przechodzenia przez ośrodek aktywny płaszczyzna polaryzacji fali nie skręca się. Rozchodzą się tam dwie fale spolaryzowane kołowo. Tak więc, ściślej mówiąc, nie mamy do czynienia ze skręcaniem, lecz ze skokiem o kąt Γ wartości azymutu dowolnie spolaryzowanej fali padającej, gdzie:

d - droga geometryczna fali w ośrodku aktywnym

γ = γ_f i γ_f - wzajemne przesunięcie fazowe obu kołowo spolaryzowanych fal własnych

λ - długość fali w próżni

W przypadku opisywanym w ćwiczeniu, światło padające na ośrodek ak­tywny jest spolaryzowane liniowo. Mamy więc do czynienia rzeczywiście ze skręceniem płaszczyzny polaryzacji, a nie ze skręceniem azymutu eliptycznego stanu polaryzacji jak w przypadku ogólnym. Zjawisko przedstawione w ćwi­czeniu przebiega w szkle wysokoołowiowym (ciężki flint), umieszczonym w polu magnetycznym solenoidu

Zjawisko Faradaya. Jeżeli w ośrodku z natury jednorodnym wytworzy się strumień indukcji magnetycznej S , to ośrodek ten staje się kołowo dwójłomny. Na długości d ciała umieszczonego w polu magnetycznym następuje wymuszone wzajemne przesunięcie fazowe o kąt γ kołowo spolaryzowanych fal własnych. Powoduje to skok azymutu stanu polaryzacji fali wychodzącej w stosunku do azymutu fali wchodzącej o kąt skręcenia Г=γ/2. Jeżeli fala biegnie wzdłuż linii indukcji magnetycznej, to obowiązuje zależność

V - stała Verdeta [rad/Tm]

d - droga geometryczna fali w ośrodku

B - indukcja magnetyczna w ośrodku

3. Przebieg ćwiczenia.

1. Układ pomiarowy

2. Tabele pomiarów

Szkło SF-1

I [A]	ΔI [A]	αP [^o]	αP [^o]	ΔαP [^o]	αL [^o]	αL [^o]	ΔαL [^o]
0,5	.........	176,60	176,75	0,07	177,90	177,82	0,04
								176,80			177,80
								176,80			177,80
								176,80			177,80
								176,80			177,80
								176,70			177,80

I [A]	ΔI [A]	αP [^o]	αP [^o]	ΔαP [^o]	αL [^o]		αL [^o]	ΔαL [^o]
1	.........	176,30	176,30	0,07	178,20	178,25		0,09
									176,20			178,20
									176,30			178,40
									176,30			178,20
									176,40			178,20
									176,30			178,30

I [A]	ΔI [A]	αP [^o]	αP [^o]	ΔαP [^o]	αL [^o]		αL [^o]	ΔαL [^o]
1,5	.........	175,80	175,69	0,08	178,90	178,92		0,04
									175,70			178,90
									175,60			178,90
									175,70			178,90
									175,60			179,00
									175,70			178,90

I [A]	ΔI [A]	αP [^o]	αP [^o]	ΔαP [^o]	αL [^o]		αL [^o]	ΔαL [^o]
2	.........	175,30	175,25	0,09	179,30	179,42		0,08
									175,40			179,40
									175,20			179,40
									175,20			179,50
									175,20			179,40
									175,20			179,50

I [A]	ΔI [A]	αP [^o]	αP [^o]	ΔαP [^o]	αL [^o]		αL [^o]	ΔαL [^o]
2,5	.........	174,50	174,52	0,04	179,90	179,85		0,06
									174,50			179,80
									174,50			179,80
									174,50			179,80
									174,60			179,90
									174,50			179,90

I [A]	ΔI [A]	αP [^o]	αP [^o]	ΔαP [^o]	αL [^o]		αL [^o]	ΔαL [^o]
3	.........	173,90	174,14	0,13	180,40	180,4		0,07
									174,20			180,30
									174,20			180,40
									174,20			180,50
									174,10			180,40
									174,20			180,40

I [A]	ΔI [A]	αP [^o]	αP [^o]	ΔαP [^o]	αL [^o]		αL [^o]	ΔαL [^o]
3,5	.........	173,60	173,55	0,09	180,90	180,87		0,06
									173,60			180,90
									173,60			180,80
									173,40			180,80
									173,50			180,90
									173,60			180,90

I [A]	ΔI [A]	αP [^o]	αP [^o]	ΔαP [^o]	αL [^o]		αL [^o]	ΔαL [^o]
4	.........	173,20	173,07	0,13	181,20	181,34		0,09
									173,20			181,40
									172,90			181,40
									173,00			181,30
									173,10			181,40
									173,00			181,30

Szkło SF-3

I [A]	ΔI [A]	αP [^o]	αP [^o]	ΔαP [^o]	αL [^o]	αL [^o]	ΔαL [^o]
0,5	.........	177,80	177,79	0,08	176,60	176,64	0,09
								177,80			176,70
								177,90			176,70
								177,70			176,70
								177,80			176,60
								177,70			176,50

I [A]	ΔI [A]	αP [^o]	αP [^o]	ΔαP [^o]	αL [^o]		αL [^o]	ΔαL [^o]
1	.........	178,50	178,44	0,06	176,00	176,1		0,09
									178,40			176,10
									178,40			176,00
									178,50			176,20
									178,40			176,10
									178,40			176,20

I [A]	ΔI [A]	αP [^o]	αP [^o]	ΔαP [^o]	αL [^o]		αL [^o]	ΔαL [^o]
1,5	.........	178,80	178,94	0,13	175,40	175,42		0,04
									178,80			175,40
									179,10			175,50
									179,00			175,40
									179,00			175,40
									178,90			175,40

I [A]	ΔI [A]	αP [^o]	αP [^o]	ΔαP [^o]	αL [^o]		αL [^o]	ΔαL [^o]
2	.........	179,50	179,47	0,06	175,00	174,97		0,06
									179,40			175,00
									179,50			174,90
									179,40			175,00
									179,50			175,00
									179,50			174,90

I [A]	ΔI [A]	αP [^o]	αP [^o]	ΔαP [^o]	αL [^o]		αL [^o]	ΔαL [^o]
2,5	.........	180,10	180,19	0,36	174,50	174,35		0,11
									180,00			174,30
									180,10			174,20
									180,00			174,40
									180,00			174,30
									180,90			174,40

I [A]	ΔI [A]	αP [^o]	αP [^o]	ΔαP [^o]	αL [^o]		αL [^o]	ΔαL [^o]
3	.........	180,60	180,64	0,11	173,90	173,87		0,06
									180,70			173,80
									180,50			173,80
									180,60			173,90
									180,80			173,90
									180,60			173,90

I [A]	ΔI [A]	αP [^o]	αP [^o]	ΔαP [^o]	αL [^o]		αL [^o]	ΔαL [^o]
3,5	.........	181,30	181,27	0,06	173,10	173,22		0,08
									181,20			173,20
									181,30			173,20
									181,30			173,30
									181,20			173,30
									181,30			173,20

I [A]	ΔI [A]	αP [^o]	αP [^o]	ΔαP [^o]	αL [^o]		αL [^o]	ΔαL [^o]
4	.........	181,60	181,75	0,09	172,50	172,60		0,11
									181,80			172,50
									181,80			172,70
									181,70			172,70
									181,80			172,50
									181,80			172,70

Przykłady obliczeń:

Przeliczenie ^o na radiany

Wzory dla

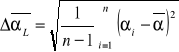
analogicznie

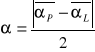
c) Wykresy:

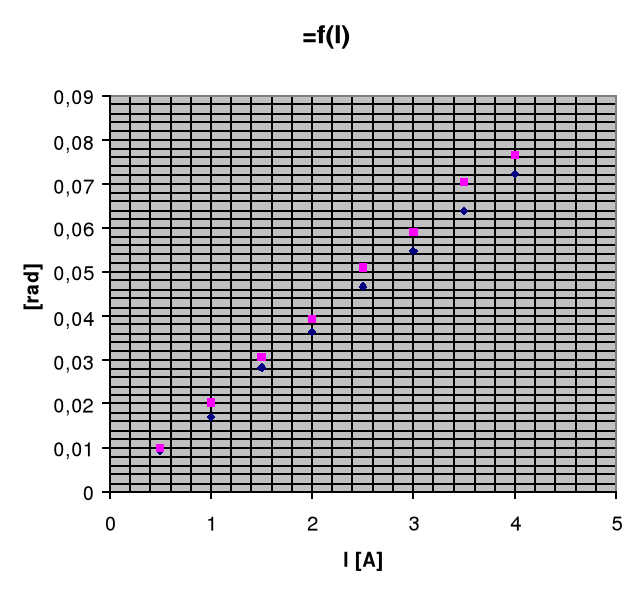
• SF -3

- SF -1d) Wyznaczenie wartości stałej Verdeta

Stałą Verdeta można wyznaczyć na podstawie danych pomiarowych i wzoru

po przekształceniu:

gdzie:

- kąt skręcenia płaszczyzn polaryzacji

- długość próbki 160,04 mm

- przenikalność magnetyczna w próżni

n - ilość zwojów solenoidu na jednostkę długości 1230zwojów / 197mm

d - długość próbki

Zauważając :

dla szkła SF-1

........................

...................

..............

...........%

...........

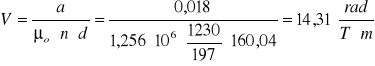
dla szkła SF-3

...............

...............

podstawiając:

............

...........%

...........

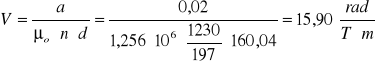
e) Obliczenie stosunku e/m - ładunku elektronu do jego masy

Korzystając ze wzoru:

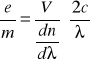
gdzie:

c - prędkość światła w próżni

- długość fali światła lampy sodowej 589,3 nm

- dyspersja

- współczynnik

obliczenia:

dla szkła SF-1

ostatecznie:

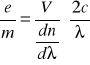
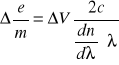
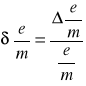
100=............%

................

dla szkła SF-3

ostatecznie:

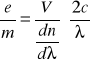
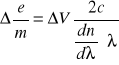
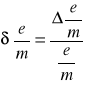
100=............%

................

4. Wnioski

Z powyższych wyników pomiarów wynika, że wielkość kąta skręcenia płaszczyzny polaryzacji jest proporcjonalna do długości badanej substancji oraz indukcji magnetycznej. Ta natomiast zależy od wielkości natężenia prądu płynącego przez solenoid. Zależność tą przedstawia wykres na którym naniesiono punkty dla obydwu próbek. W trakcie badania zjawiska, pomiaru dokonywaliśmy dla dwóch polaryzacji solenoidu. W zależności od kierunku prądu zmieniał się również kierunek zmiany kąta skręcenia. Im większe natężenie prądu tym większy kąt.

Dzięki obliczeniu zależności kąta skręcenia płaszczyzny polaryzacji od prądu płynącego przez cewkę (solenoid) mogliśmy również wyznaczyć stałą Verdeta.

Wyznaczenie stałej Verdeta umożliwiło obliczenie stosunku ładunku do masy elektronu (e/m).

---