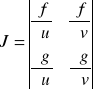
Odwzorowanie nazywamy regularnym, gdy funkcje f i g spełniają następujące warunki:

a) każdej parze wartości parametrów u, v przyporządkowują jedną i tylko jedną parę wartości parametrów U, V;

b) są ciągłe i co najmniej dwukrotnie różniczkowalne;

c) są wzajemnie niezależne,

co ma miejsce wtedy, gdy wyznacznik:

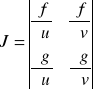
zwany jakobianem układu :

U = f(u,v)

V = g(u,v),

jest różny od zera dla wszystkich par wartości u, v.

W odwzorowaniach regularnych, obrazem:

punktu jest punkt,

krzywej jest krzywa,

kąta jest kąt,

obszaru jest obszar.

Obrazem krzywych mających wspólną styczną w punkcie P są krzywe mające także wspólną styczną w obrazie punktu P'.

Jeżeli oryginałem jest cała powierzchnia elipsoidy obrotowej lub jej część, to rolę parametrów u v odgrywają zwykle :współrzędne elipsoidalne B, L. Jeżeli rolę parametrów u, v odgrywają współrzędne prostokątne x, y, to funkcje odwzorowawcze mają postać:

x = x (B, L)

y = y (B, L)

Jeżeli położenie punktu na płaszczyźnie opisują biegunowe p, ó, to funkcje odwzorowawcze mają postać:

p = p (B, L)

ó = ó (B, L)

W kartografii szczególne znaczenie mają obrazy południków i równoleżników tworząc siatkę kartograficzną