1.OPIS TEORETYCZNY
Dipolem elektrycznym nazywamy układ dwóch przeciwnych ładunków elektrycznych umieszczonych w pewnej odległości od siebie.
Punkt A, w którym skupiony jest ładunek dodatni nazywamy biegunem dodatnim, a punkt B - biegunem ujemnym. Iloczyn bezwzględnej wartości ładunku jednego z biegunów dipola i odległości l między biegunami nazywamy momentem dipolowym : ![]()
Wielkość tę interpretujemy wektorowo. Przypisujemy jej mianowicie kierunek wzdłuż osi i zwrot od bieguna ujemnego ku dodatniemu. Pojęcie dipola można stosować do więcej niż dwóch ładunków pod warunkiem, że suma algebraiczna wszystkich ładunków równa się zeru i środki ciężkości ładunków przeciwnego znaku nie pokrywają się. Cząsteczka wody jest dipolem, ponieważ nie ma struktury liniowej, lecz kątową.
Przypisuje się jej promień równy 0,138 nm. Niektóre cząsteczki dielektryków nie mają momentu dipolowego. Nazywamy je niespolaryzowanymi. Aby zaobserwować zjawisko polaryzacji dielektryka należy wprowadzić go w obszar pola elektrycznego (np. pomiędzy okładki naładowanego kondensatora). W ogólnym przypadku mogą zachodzić trzy zjawiska:
Jeżeli cząsteczka jest dipolem elektrycznym wówczas na jej biegun dodatni działa siła culombowska skierowana wzdłuż przechodzących przez ten punkt linii sił pola elektrycznego w kierunku z nimi zgodnym, na biegun ujemny zaś siła o zwrocie przeciwnym. Ta para sił stara się ustawić tę cząsteczkę tak, aby jej oś była położona wzdłuż linii sił pola elektrycznego i charakteryzowała się minimalną energią potencjalną. Zjawisko to nazywamy polaryzacją skierowaną . W pełnym uporządkowaniu cząsteczek przeszkadza ruch cieplny rosnący wraz z temperaturą.
W polu elektrycznym na dodatnie jądra atomowe działają siły przesuwające je wzdłuż linii sił pola elektrycznego zgodnie z ich zwrotem, natomiast elektrony w stronę przeciwną. Ze względu na małą masę przesunięciu ulegają głównie elektrony powodując deformację powłok elektronowych. Zjawisko to nazywamy polaryzacją elektronową . Po zaniku działania pola elektrycznego deformacja znika i cząsteczki tracą swoją biegunowość.
Atomy lub grupy polarne cząsteczki pod wpływem zewnętrznego pola elektrycznego ulegają przesunięciu lub obrotowi. Zjawisko to nazywamy polaryzacją jonową.
Zjawisko polaryzacji jest sumą trzech omówionych procesów, przy czym zjawisko drugie i trzecie występuje w cząsteczkach wszystkich substancji, a pierwsze tylko w substancjach polarnych.
W ten sposób całkowita polaryzowalność substancji (α) jest sumą trzech polaryzowalności: skierowanej (α sk), jonowej (αj), elektronowej (αe):
α= α sk+ αj+ αe
Równanie Clausiusa-Mosottiego określa zależność polaryzowalności substancji z jej stałą dielektryczną (ε):
![]()
gdzie : M - masa cząsteczkowa substancji,
r - gęstość substancji,
NA- liczba Avogadra.
Aby wyznaczyć elektronową polaryzowalność substancji należy wykorzystać różną bezwładność poszczególnych procesów tak aby wyeliminować wpływ polaryzowalności jonowej i skierowanej. Umieszczając substancję w zmiennym polu elektrycznym stwierdzamy, że wpływ polaryzowalności skierowanej zanika przy częstotliwości rzędu 1010-1012 Hz, a polaryzowalności jonowej już przy częstotliwości 1014-1015 Hz. Więc aby wyeliminować
wpływ polaryzowalności skierowanej i jonowej należy substancję np. oświetlić widzialną falą elektromagnetyczną. Jeżeli ośrodek nie jest ferromagnetyczny (przenikalność magnetyczna zbliżona do1) jego współczynnik załamania wyraża się wzorem wynikającym z teorii Maxwella:
![]()
a więc
![]()
Stosując równanie Clausiusa-Mosottiego tylko dla polaryzowalności elektronowej i uwzględniając powyższy wzór otrzymujemy wyrażenie na polaryzowalność elektronową:
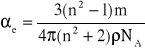
3. OPRACOWANIE ĆWICZENIA
WYKRESY
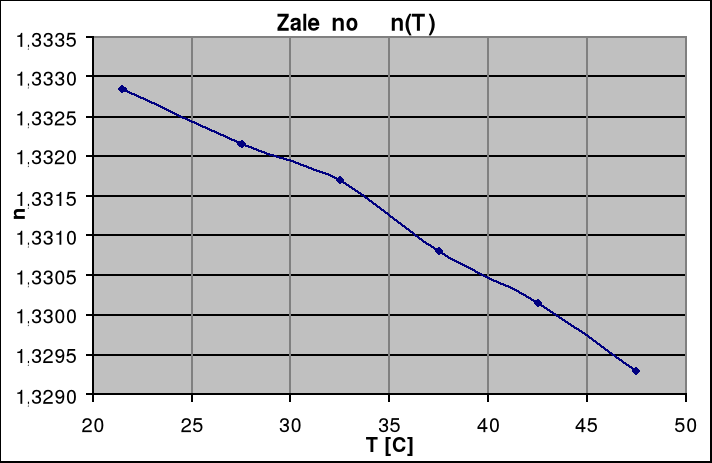
Wykres 1.
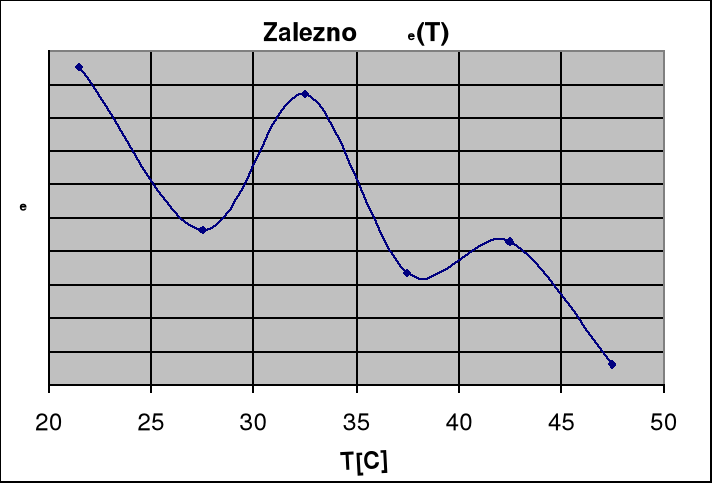
Wykres 2.
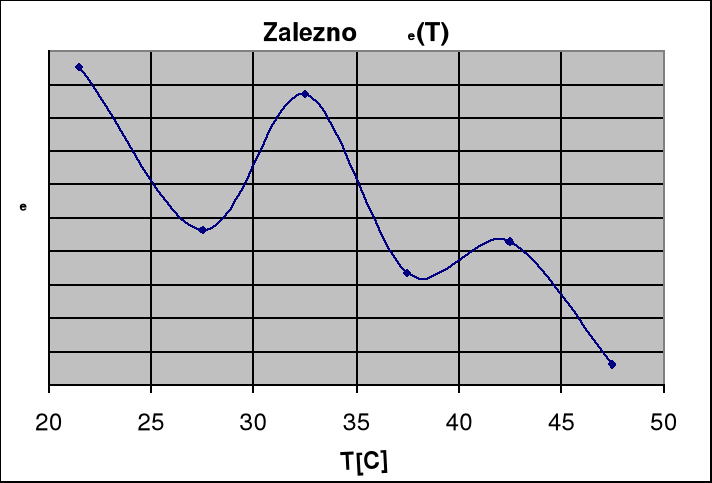
WARTOŚĆ POLARYZOWALNOŚCI WODY
Wartości gęstości wody odczytane z tabeli oraz średni współczynnik załamania światła n
T[C°] |
ρ[g/cm3] |
nsrednie |
21,5 |
0,99791 |
1,33285 |
27,5 |
0,99668 |
1,33215 |
32,5 |
0,99489 |
1,33170 |
37,5 |
0,99318 |
1,33080 |
42,5 |
0,99127 |
1,33015 |
47,5 |
0,98918 |
1,32920 |
Liczba Avogadra NA= 6,022*10 23 mol-1
Masa cząsteczkowa wody m=18 g/mol
Kolejno podstawiam wszystkie wartości podane powyżej do wzoru na polaryzowalność:
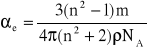
[m3]
i otrzymuje :
dla T= |
21,5 C° |
Mamy αe = |
1,45110*10-30 |
dla T= |
27,5 C° |
Mamy αe = |
1,45013*10-30 |
dla T= |
32,5 C° |
Mamy αe = |
1,45094*10-30 |
dla T= |
37,5 C° |
Mamy αe = |
1,44987*10-30 |
dla T= |
42,5 C° |
Mamy αe = |
1,45006*10-30 |
dla T= |
47,5 C° |
Mamy αe = |
1,44932*10-30 |
- Graniczny błąd wyznaczenia gęstości wody
![]()
gdzie i = 2...6 i ΔT=0,1
Δρ2= -0,000021
Δρ3= -0,000036
Δρ4= -0,000034
Δρ5= -0,000038
Δρ6= -0,000042
maksymalna z tych wartości jest błędem granicznym : |Δρ|=0,0004 g/cm3
WZGLĘDNY BŁĄD GRANICZNY POLARYZOWALNOŚCI αe DLA T= 21,5 C°
![]()
BEZWZGLĘDNY BŁĄD GRANICZNY Δαe
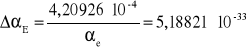
m3
4. WNIOSKI I OCENA REZULTATÓW
Wyznaczona polaryzowalność elektronowa cząsteczki wody wynosi:
Dla T= 21,5 C° => αe=1,45110*10-29 ± 5,18821*10-33[m3]; błąd względny Δαe=±4,20926*10-4
Dla T= 27,5 C° => αe=1,45013*10-29 ± 5,17749*10-33[m3];; błąd względny Δαe=±4,20056*10-4
Dla T= 32,5 C° => αe=1,45094*10-29 ± 5,15084*10-33[m3];; błąd względny Δαe=±4,17894*10-4
Dla T= 37,5 C° => αe=1,44987*10-29 ± 5,11090*10-33[m3];; błąd względny Δαe=±4,14653*10-4
Dla T= 42,5 C° => αe=1,45006*10-29 ± 5,06375*10-33[m3];; błąd względny Δαe=±4,10828*10-4
Dla T= 47,5 C° => αe=1,45932*10-29 ± 5,01266*10-33[m3];; błąd względny Δαe=±4,06683*10-4
Przeprowadzone przeze mnie doświadczenie jest praktycznym dowodem na to, że współczynnik załamania światła jest zależny niemalże liniowo od temperatury (wykres 1.). Wyniki pomiarów wykazały to w dostatecznym stopniu. Doświadczenie wykazało także, iż polaryzowalność elektronowa wody praktycznie nie zależy od temperatury (wykres 2.). Różnica wyników mieści się w granicy błędu. Jest tak ponieważ dipole zwane indukowanymi (istniejące tylko w zewnętrznym polu) ustawiają się zawsze zgodnie z liniami sił pola elektrycznego niezależnie od ruchu cieplnego i związanej z nią temperatury. Ćwiczenie potwierdziło także wyeliminowanie wpływu polaryzacji skierowanej i jonowej poprzez odpowiedni dobór częstotliwości pola zewnętrznego (widzialne fale elektromagnetyczne). Wynika to z tego, że wyniki pomiarów z dość dobrym przybliżeniem nie zależą od temperatury, a zależałyby gdyby na wyniki miały wpływ polaryzacje skierowana i jonowa, które zależą od ruchów cieplnych. Ogólnie dokładność pomiarów oceniam na dość dobrą, a błędy w wyznaczeniu elektronowej polaryzowalności wody spowodowane są nałożeniem się błędów odczytu temperatury ΔT=0.1 CO, błędu odczytu współczynnika załamania Δn=0.0001 a także gęstości wody.
+q
-q
![]()
l
A
B
0,096 nm
0,154 nm
0
-2δ
H+δ
H+δ
μOH
μOH
![]()
105o
Wyszukiwarka