7. Porządkowanie danych i taksonomia

7.1. Uwagi wstępne

Nazwa „taksonomia” pochodzi od dwóch greckich określeń „taksis” - układ, porządek i „nomos” - prawo i oznacza naukę o zasadach porządkowania i klasyfikacji. Tego typu przedsięwzięcia znane były od bardzo dawna i zawsze stanowiły jeden z podstawowych elementów porządkowania wiedzy o otaczającym człowieka świecie. Swoiste mistrzostwo osiągnęli w takich działaniach intelektualnych filozofowie greccy, a zwłaszcza Arystoteles. Wiele ich również w średniowiecznej myśli teoretycznej i filozoficznej czy w przełomowych odkryciach naukowej myśli odrodzeniowej. Pierwsze próby porządkowania o wyraźnym charakterze taksonomicznym pojawiły się jednak w naukach biologicznych, w XVIII stuleciu i związane były z K.Linneuszem. Także w tym stuleciu botanik angielski M.Adanson sformułował podstawowe postulaty, jakie powinna spełniać taksonomia. W nowoczesny sposób, za R.Sokalem i P.Sneathem, można je określić następująco:

1. najlepszą taksonomią jest taka, w której dana wyodrębniona klasa zawiera największą ilość informacji i opiera się na możliwie największej liczbie cech;

2. każda cecha ma równą a priori wagę przy tworzeniu naturalnej klasy;

3. ogólne podobieństwo obiektów w zbiorze jest funkcją podobieństwa wszystkich uwzględnionych cech;

4. odrębną klasę można tworzyć na podstawie odmiennego charakteru zależności między obiektami należącymi do różnych klas;

5. taksonomia w powyższym znaczeniu jest nauką empiryczną;

6. podobieństwo miedzy obiektami badane jest bez uwzględniania historycznych zmian obiektów.

Taksonomia wzbudzała szerokie zainteresowanie metodologów nauki, którzy upatrywali w niej bardzo ważnej formy aktywności badawczej. W.S.Jevons sformułował kilka postulatów logicznych, które należy brać pod uwagę w trakcie procedury klasyfikacyjnej. Po pierwsze, zdaniem W.S.Jevonsa, klasyfikacja to elementarna przesłanka wszelkich rozważań znajdujących się u podstaw wiedzy. Po drugie, wyodrębnione człony klasyfikacji powinny stwarzać możliwość na dokonywanie uogólnień indukcyjnych. Po trzecie, każda klasyfikacja powinna być realizowana na podstawie jednoznacznie określonych kryteriów. Po czwarte, najbardziej wartościowa jest taka klasyfikacja, która jest zgodna z systemem naturalnym, to znaczy, odpowiada jak największej liczbie celów. Po piąte, każda klasyfikacja jest związana z polem obserwacji, co oznacza, że jest (może być i powinno) wiele systemów klasyfikacji badanego zjawiska.

Taksonomia, jak już wspomniano, była początkowo wykorzystywana w botanice i zoologii, później antropologii, skąd została przeniesiona do badań geograficznych, psychologicznych, socjologicznych i ekonomicznych. Współcześnie taksonomiczne metody klasyfikacji wykorzystuje się w wielu dziedzinach nauki, zwłaszcza w geografii, antropologii i naukach ekonomicznych. Metody taksonomiczne znalazły w ostatnich trzydziestu latach liczne zastosowania w różnorodnych badaniach społeczno-ekonomicznych. Można je stosować do zagadnień prostych, złożonych i kompleksowych. W ramach zagadnień prostych pierwszym jest grupowanie obiektów. Polega ono na grupowaniu obiektów jednocechowych lub wielocechowych w danej jednostce czasu (np. roku kalendarzowym. Przykładem takiego zadania jest grupowanie firm według wielkości produkcji w danym roku kalendarzowym lub w pewnym okresie, czy grupowanie firm w danym roku kalendarzowym lub okresie przy uwzględnieniu wielkości produkcji, rozmiarów zatrudnienia i wielkości posiadanego kapitału. Drugim zagadnieniem prostym jest periodyzacja, polegająca na grupowaniu jednostek czasu przy określonej liczbie obiektów i wartości cech. Periodyzacja może być zatem wyodrębnienie okresów, w których stan obiektów, określany wartością cech lub ich przekształceń jest podobny lub wyodrębnienie faz rozwojowych czyli podział szeregu czasowego na segmenty. Trzecim zagadnieniem prostym jest wybór cech diagnostycznych. Pozwala on na wyodrębnienie takiego wektora nośników informacji o możliwie niewielkiej liczbie składowych, który w największym stopniu (ze względu na założone kryterium) wyjaśnia zmienność obiektów.

W ramach zagadnień złożonych wyróżnić możemy klasyfikację w przestrzeni cech, obiektów i czasu. Przykładem pierwszej klasyfikacji może być wyróżnienie obiektów w pewnych okresach czasu podobnych ze względu na kształtowanie się rozmiarów (poziomu) cech (np. gminy podobne ze względu na emisje podstawowych zanieczyszczeń środowiska przyrodniczego). Przykładem klasyfikacji w przestrzeni obiektów jest wyróżnienie tych cech (opisujących np. oddziaływanie społeczności lokalnych na środowisko przyrodnicze) w pewnym okresie czasu, dla których gminy były podobne. Natomiast przykładem klasyfikacji w przestrzeni czasu jest podział, w ramach którego wyróżni się cechy i gminy wykazujące podobną zmienność w pewnym badanym okresie. Zagadnienie kompleksowe obejmuje łączne porządkowanie obiektów, cech oraz jednostek czasu. Przykładem takiego zadania jest określenie, które gminy, w jakim okresie (w jakich latach) i ze względu na jakie cechy tworzyły jednorodne grupy.

Metody taksonomiczne są szczególnie często wykorzystywane w przestrzennych, porównawczych badaniach społeczno-ekonomicznych. Chodzi tu przede wszystkim o międzynarodowe porównania rozwoju społeczno-gospodarczego krajów świata, badania poziomu rozwoju społeczno-gospodarczego wybranych jednostek administracyjnych (np. gmin czy województw), analizę warunków życia ludności czy rozwoju rynków lub stanu środowiska przyrodniczego, a także o rejonizację ekonomiczno-rolniczą czy badania efektywności działania firm.

Badania nad rozwojem społeczno-gospodarczym państw świata rozpoczął w 1968 roku Z.Hellwig i zespół wrocławski. Rozwinięte zostały później przez zespół krakowski A.Zeliasia. Po nowym podziale administracyjnym Polski z 1975 roku rozwinęły się prace, w których badano poziom rozwoju społeczno-gospodarczego dla województw czy gmin. W latach siedemdziesiątych i osiemdziesiątych pojawiły się liczne studia, w ramach których, za pomocą metod taksonomicznych, dokonywano między innymi oceny poziomu zaspokojenia potrzeb wyżywieniowych, wyodrębnienia rejonów konsumpcji, rozwoju usług rynkowych, oceny poziomu życia ludności wiejskiej czy rejonizację ekonomiczno-rolniczą kraju. Badano również efektywność działania firm, a niektóre metody taksonomiczne wykorzystywano w badaniach jakości. W latach dziewięćdziesiątych pojawiają się próby wykorzystania metod taksonomicznych do klasyfikacji regionów o różnym poziomie antropogenicznej presji na środowisko przyrodnicze, różnym stanie (jakości) środowiska przyrodniczego, wyodrębniania regionów zagrożenia ekologicznego czy analizy poziomu ekorozwoju.

Istnieje bardzo rozległa literatura w tym zakresie i coraz częściej mówi się o odrębnej dyscyplinie nauki jaką jest taksologia, która, według T.Borysa, jest nauką o porządkowaniu i klasyfikacji. Obok taksologii wyróżnia on taksonomię, rozumianą jako opisowy dział taksologii, formułujący jej cele, prawa-zasady, metodykę i semantykę oraz taksonometrię, która jest formalnym działem taksologii, zajmującym się wykorzystaniem metod ilościowych w taksonomii.

7.2. Metody taksonomiczne - podstawowe pojęcia i procedura badawcza

Taksonomiczne metody klasyfikacji polegają przede wszystkim na szeregowaniu i porządkowaniu obiektów znajdujących się w wielowymiarowej przestrzeni. Wymiar przestrzeni określany jest liczbą cech charakteryzujących jednostki badanej zbiorowości. Podstawowym pojęciem służącym klasyfikacji jest „odległość taksonomiczna”. Jest to liczona zgodnie z regułami geometrii analitycznej odległość między punktami (obiektami) wielowymiarowej przestrzeni.

Porządkowanie może mieć charakter liniowy i nieliniowy. Pierwszy typ polega na rzutowaniu przestrzeni wielowymiarowej na prostą, drugi natomiast na rzutowaniu na płaszczyznę. Analiza taksonomiczna może być również wykorzystywana dla porównania podobieństwa obiektów do wzorca. Wykorzystujemy wówczas porządkowanie obiektów przy wykorzystaniu taksonomicznego miernika rozwoju.

Potrzeba klasyfikowania zbiorów wynika z kilku istotnych powodów. Po pierwsze, pomaga to w analizie zjawisk, ułatwiając odkrycie związków przyczynowo-skutkowych i wyciągnięcie określonych wniosków (wymiar metodologiczny). Po drugie, klasyfikacja zmniejsza szum informacyjny, dając możliwość łatwiejszej orientacji w dużych jej zasobach (wymiar poznawczy). Po trzecie, redukcja ilości informacji pozwala zmniejszyć koszty rzeczowe i nakłady czasu na badania (wymiar ekonomiczny).

Do elementarnych pojęć używanych w taksonomii zaliczyć można pojęcie obiektu, cechy, podobieństwa, jednorodności i klasy. Obiektami są jednostki badania podlegające klasyfikacji. Przykładami obiektów mogą być podmioty gospodarujące, jednostki administracyjne, wyroby, osoby czy jednostki czasu. Przedmiotem klasyfikacji jest zbiór obiektów Ω. Cechami są właściwościami poszczególnych obiektów, które analizujemy ze względu na kryterium klasyfikacji obiektów. Jeżeli na przykład, chcemy poklasyfikować gminy województwa wałbrzyskiego ze względu na stan środowiska przyrodniczego, wówczas cechami mogą być: imisja dwutlenku siarki, stopień zanieczyszczenia wód powierzchniowych, powierzchnia terenów zdegradowanych itp. W taksonomii używa się także pojęcia podobieństwo, jednorodność i klasa. Podobieństwo oznacza wspólność (zbieżność) pewnych cech dwóch lub więcej obiektów, jednorodność to własność zbioru obiektów składającego się z jednostek podobnych. Klasa to podzbiór zbioru Ω składająca się z obiektów podobnych.

Podstawową czynnością taksonomii jest klasyfikacja. Jak zauważa E.Nowak ma ona trzy znaczenia. „W pierwszym znaczeniu klasyfikacja oznacza czynność podziału zbioru obiektów na podzbiory według ustalonego kryterium, drugim - efekt czynności podziału zbioru, którym są grupy obiektów podobnych... Trzecie znaczenie pojęcia klasyfikacja występuje w statystyce i oznacza ono klasyfikację obserwacji, tzn. decyzje, do której klasy ze zbioru zadanych zaliczyć obserwację”. Klasyfikację można przedstawić formalnie w sposób następujący. Zbiór Ω, składający się z N obiektów, opisywanych przez K cech diagnostycznych można podzielić na P klas - A₁, A₂, ..., A_P, gdzie 1 ≤ P ≤ N, tak, że:

1. A₁∪A₂∪...∪A_P, = Ω

2. A_P∩A_q = ∅ (p,q = 1,2,...,P, p≠q)

3. A_p ≠ ∅ (p=1,2,...,P).

Liczba grup typologicznych P jest zwykle nieznana. Poza powyższymi formalnymi warunkami klasyfikacja powinna dodatkowo spełniać następujące warunki:

- obiekty tworzące daną klasę powinny być jak najbardziej do siebie podobne;

- obiekty z różnych klas powinny natomiast być jak najmniej podobne do siebie.

Cała procedura badania taksonomicznego przebiega według następujących etapów:

1. wstępna analiza badanego systemu;

2. dobór cech diagnostycznych i skal ich pomiaru;

3. zgromadzenie danych statystycznych;

4. ocena podobieństwa klasyfikowanych obiektów;

5. wybór metody klasyfikacji;

6. klasyfikacja obiektów;

7. weryfikacja wyników klasyfikacji;

8. interpretacja wyników.

W pierwszym etapie określa się podstawowe cele badania, obiekty podlegające klasyfikacji oraz przedział lub moment czasu objętego badaniem taksonomicznym. Należy także sformułować wstępne hipotezy badawcze. Wybory dokonane na tym etapie i podjęte wówczas decyzje określają charakter i kierunki całego dalszego postępowania analitycznego. W etapie drugim dobiera się cechy diagnostyczne opisujące obiekty. Jest to bardzo ważny moment badań. Należy bowiem dobrać taki zestaw (zbiór) tych cech, aby one opisywały w najbardziej adekwatny sposób. Jak zauważa E.Nowak, „Badaniu diagnostyczności cech służą metody statystyczne. Statystyczny dobór cech diagnostycznych umożliwia wykrycie istotnych charakterystyk badanego zjawiska i eliminację wielkości będących nośnikami informacji zbyt przypadkowych i szczegółowych”. Etap trzeci to zbieranie odpowiednich danych statystycznych. Problem pojawia się, gdy zgromadzony zbiór informacji nie jest kompletny. Wówczas musimy stosować specjalne metody postępowania badawczego. Efektem końcowym tego etapu powinna być kompletna macierz obserwacji. Czwarty etap to statystyczna ocena podobieństwa klasyfikowanych jednostek. Nie jest to problem prosty, ponieważ klasyfikacje przeprowadza się często na podstawie wielu różnych cech, wśród których może wystąpić konflikt wskazań. Oznacza to, że jedna cecha dla obiektu pierwszego jest większa niż dla drugiego, druga natomiast kształtuje się odwrotnie. Syntetyczną ocenę podobieństwa przeprowadza się na podstawie różnie definiowanych miar podobieństwa. Podstawowymi problemami są tutaj: normalizacja cech, wybór systemu cech diagnostycznych oraz wybór miary podobieństwa. Etap piąty to wybór metody klasyfikacji. Jest to ważne z dwóch powodów. Po pierwsze, istnieje obecnie wiele różnorodnych metod taksonomicznych. Wybór powinien być zatem dokonany przy uwzględnieniu charakteru badania i stawianych przed nim celów. Po drugie, wyniki klasyfikacji pozostają w pewnej zależności od zastosowanej metody. Należy zatem brać pod uwagę ten fakt, zwłaszcza gdy chcemy aby badania nie prowadziły do „manipulowanych” wyników. Etap szósty to właściwa klasyfikacja obiektów. Etap siódmy, w trakcie którego weryfikuje się uzyskane wyniki klasyfikacji odgrywa szczególna rolę w badaniu taksonomicznym. Jest bowiem swoistym podsumowaniem i sprawdzeniem poprawności całej procedury badawczej. Wykorzystuje się w nim zarówno metody statystyczne, jak i przede wszystkim wiedzę prowadzącego badania. Badania kończy etap ósmy, w ramach którego następuje merytoryczna interpretacja wyników klasyfikacji oraz ich praktyczne wykorzystanie.

Przy klasyfikacji obiektów możemy wykorzystać diagram Czekanowskiego lub metodę dendrytową. Budowa diagramu Czekanowskiego polega na obliczeniu macierzy odległości i przeprowadzeniu podziału na klasy o ustalonych z góry przedziałach. Klasom tym przyporządkowuje się określone znaki graficzne. Klasie o najmniejszych wartościach liczbowych przyporządkujemy kolor czarny, kolor szary klasie następnej, linie poziome klasie kolejnej, linie pionowej kolejnej, a kratkę klasie ostatniej, do której wchodzą obiekty najbardziej zróżnicowane. Otrzymujemy w ten sposób nieuporządkowany diagram Czekanowskiego, ponieważ nie wydzieliły się jednostki najbardziej do siebie podobne. Aby diagram uporządkować należy tak przestawiać kolumny i wiersze, aby znaki czarne, symbolizujące obiekty najbardziej podobne znalazły się w pobliżu przekątnej. Wówczas możemy zorientować się ile grup obiektów podobnych powstało i ile każda z nich liczy elementów.

Schemat 7.1. Przykład diagramu Czekanowskiego

Numery jednostek	1	2	3	4	5	6
1
2
3
4
5
6

Źródło: opracowanie własne na podstawie literatury

Metoda dendrytów polega na nieliniowym uporządkowaniu obiektów, w taki sposób, że nie są one uszeregowane jeden za drugim, lecz pogrupowane w pewne zbiory, o różnej lub jednakowej liczbie elementów. W metodzie tej wykorzystywane jest pojecie dendrytu, łamanej „która może się rozgałęziać, lecz nie może zawierać łamanych zamkniętych i taką, że każde dwa punkty zbioru Z są przez nią połączone”. Przy uporządkowaniu liniowym poszczególne obiekty układają się w pewnej kolejności, jeden za drugim. W przypadku uporządkowania nieliniowego mogą tworzyć się różnorodne kombinacje ułożeń. Za lepsze uważa się to, którego suma długości wiązadeł jest mniejsza. Punktem wyjścia metody dendrytowej jest sporządzenie macierzy odległości. Informacja w niej zawarta opisuje badane obiekty w ten sposób, że elementy znajdujące się w j-tej kolumnie są odległościami j-tego obiektu od wszystkich pozostałych obiektów. Gdybyśmy chcieli znaleźć obiekt najmniej różniący się od j-tego to trzeba znaleźć najmniejszą liczbę w j-tej kolumnie. Wiersz zawierający znalezioną liczbę jest oznaczony numerem tego najbliższego obiektu. W pierwszym etapie tworzymy połączenia wszystkich badanych obiektów z najbliższymi. Ponieważ w dendrycie kolejność połączeń nie ma znaczenia, możemy wyeliminować połączenia podwójne. Następnie łączymy w całość te wszystkie pary połączeń, w których występują identyczne obiekty. Jest to tzw. skupienie pierwszego rzędu. Jeżeli otrzymane skupienia nie są połączone w jedną całość, wówczas musimy utworzyć skupienie drugiego rzędu, polegające na wyborze najmniejszej odległości między obiektami skupień pierwszego rzędu. Postępowanie to kończymy w momencie, kiedy każde dwa obiekty badanego zbioru są ze sobą połączone. Otrzymujemy w ten sposób dendryt. Pokazuje on nie tylko pewien sposób uporządkowania zbioru, ale dodatkowo pozwala dokonać klasyfikacji. Może ona przebiegać według kryterium znanej z góry liczby części lub klasyfikacji na dowolną, z góry nie znaną liczbę grup. Przy pierwszym podejściu z rozpiętego dendrytu usuwamy n-1 najdłuższych wiązadeł. Przy drugim, procedura postępowania jest następująca: 1) porządkujemy według malejących wartości wszystkie łuki dendrytu, 2) tworzymy ilorazy długości sąsiednich łuków według formuły:

7.1.

gdzie: d₁, d₂, d_t-1 - uporządkowane długości łuków, w₂, w₃, ..., w_t-1 - ilorazy długości łuków. Kryterium podziału jednostek na n części następuje według relacji:

w_n < w_n+1 dla n = 2,3,..., t-1 7.2.

Jeżeli wśród obliczonych ilorazów kilka razy jest spełnione powyższe kryterium, to podajemy dodatkowy warunek podziału. Z dwóch klasyfikacji lepsza jest ta, dla której:

w_n < w_m 7.3.

7.3. Zastosowanie metod taksonomicznych

Rozwiązywanie podstawowego problemu taksonomicznego, jakim jest klasyfikacja obiektów, rozpoczyna się od utworzenia macierzy obserwacji. Charakteryzuje ona poszczególne obiekty za pomocą zespołu cech. Załóżmy, że zbiór liczy t obiektów, z których każdy jest opisywany przez k cech. Oznacza to, że każdy obiekt jest punktem k-wymiarowej przestrzeni. Macierz obserwacji możemy zapisać w postaci:

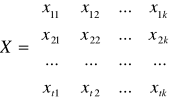
7.4.

gdzie: t - ilość obiektów zbioru, k - ilość cech, x_ij - wartość j-tej cechy w i-tym obiekcie.

Przykład 7.1. Przygotowanie macierzy obserwacji polega na doborze odpowiednich cech charakteryzujących dany obiekt. Poniżej mamy tablicę (macierz), w której zgromadzono pewne informacje charakteryzujące wybrane gminy z regionu wałbrzyskiego.

Tabela 7.1. Macierz potencjalnych zmiennych charakteryzujących wybrane obiekty (gminy)

Cechy (j) Obiekt (i)	Dochód na osobę (tys. zł) (j=1)	Liczba samochodów na rodzinę (sztuk) (j=2)	Liczba osób na izbę mieszkalną (sztuk) (j=3)	Wyposażenie gosp. dom. w sprzęt AGD i RTV (sztuk na gospodarstwo) (j=4)	Liczba mieszkańców (tys. osób) (j=5)	Liczba kupionych rocznie książek (szt. na os.) (j=6)	Powierzchnia gminy (km^2) (j=7)
Wałbrzych (i=1)	0,825	0,92	1,2	3,1	140	4,1	85
Nowa Ruda (i=2)	0,718	0,85	1,6	3,2	28	1,6	37
Boguszów Gorce (i=3)	0,702	0,63	1,4	3,3	19	1,2	27
Świdnica (i=4)	0,995	1,12	1,3	3,2	65	4,7	22
Kłodzko (i=5)	0,811	0,83	1,4	3,4	31	2,6	25

Źródło: dane umowne

Cechy piąta i siódma, czyli liczba mieszkańców w tysiącach osób oraz powierzchnia gminy w km² są przedstawione jako wielkości absolutne a dodatkowo trudno znaleźć bezpośredni ich związek z poziomem rozwoju społecznego, nie powinny znajdować się w macierzy obserwacji. Z tych powodów macierz obserwacji powinna mieć postać.

Tabela 7.2. Macierz obserwacji zmiennych charakteryzujących wybrane obiekty (gminy)

Cechy (j) Obiekt (i)	Dochód na osobę (tys. zł) (j=1)	Liczba samochodów na rodzinę (sztuk) (j=2)	Liczba osób na izbę mieszkalną (sztuk) (j=3)	Wyposażenie gosp. dom. w sprzęt AGD i RTV (sztuk na gosp.) (j=4)	Liczba kupionych rocznie książek (szt. na os.) (j=6)
Wałbrzych (i=1)	0,825	0,92	1,2	3,1	4,1
Nowa Ruda (i=2)	0,718	0,85	1,6	3,2	1,6
Boguszów Gorce (i=3)	0,702	0,63	1,4	3,3	1,2
Świdnica (i=4)	0,995	1,12	1,3	3,2	4,7
Kłodzko (i=5)	0,811	0,83	1,4	3,4	2,6

Źródło: dane umowne

Interpretacja: macierz obserwacji będą tworzyć zmienne (cechy) charakteryzujące bezpośrednio badane zjawisko złożone czyli: (1) dochód na osobę w tysiącach złotych, (2) liczba samochodów na rodzinę w sztukach, (3) liczba osób przypadająca na jedną izbę mieszkalną, (4) wyposażenie gospodarstwa domowego w sprzęt AGD i RTV w sztukach oraz (5) liczba zakupionych książek na osobę w sztukach.

Macierz obserwacji musi być skonstruowana w taki sposób, aby ujednolicić jednostki miary cech i ujednolicić rzędy wielkości cech. Można to zrobić poprzez standaryzację lub unitaryzację. Standaryzację można zrealizować według formuły:

7.5.

gdzie:

7.6.

natomiast

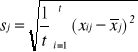
7.7.

x_ij - wartość j-tej cechy w i-tym obiekcie, s_j - odchylenie standardowe j-tej cechy, z_ij - standaryzowana wartość j-tej cechy w i-tym obiekcie. Po przeprowadzeniu operacji standaryzacji cech macierz obserwacji przyjmuje postać:

7.8.

Po standaryzacji mamy niemianowane wartości wszystkich cech. Proces standaryzacji powoduje, że wszystkie cechy są ujednolicone ze względu na zmienność i położenie w przestrzeni obserwacji, o czym świadczy fakt, że dla zestandaryzowanych cech, średnia arytmetyczna wynosi zero a wariancja i odchylenie standardowe są równe jedności.

Przykład 7.2. Standaryzacja ma uporządkować informacje zawarte w macierzy obserwacji ze względu na ich zmienność. Przebiega ona w kilku etapach. Etap pierwszy - wyznaczenie średnich arytmetycznych dla poszczególnych cech. Do tego celu wykorzystujemy formułę 7.6.

j =

0,81

0,87

1,38

3,24

2,84

Etap drugi - wyznaczenie odchyleń standardowych dla poszczególnych cech na podstawie formuły 7.7.

Sj

0,104

0,16

0,13

0,1

1,37

Etap trzeci - wyznaczenie wartości zestandaryzowanych z_ij macierzy Z. Opieramy się na formule 7.5. Wartości zestandaryzowane cechy pierwszej:

z₁₁ =
= 0,144

z₂₁ =
= -0,885

z₃₁ =
= -1,038

z₄₁ =
= 1,779

z₅₁ =
= 0,01

Wartości zestandaryzowane cechy drugiej:

z₁₂ =
= 0,313

z₂₂ =
= -0,125

z₃₂ =
= -1,5

z₄₂ =
= 1,563

z₅₂ =
= -0,25

Analogicznie postępujemy z pozostałymi wartościami cech dla obiektów. Etap czwarty - budowa macierzy zestandaryzowanej Z.

i j	j=1	j=2	j=3	j=4	j=5
i=1	0,144	0,313	-0,6	-1,4	0,92
i=2	-0,885	-0,125	0,73	-0,4	-0,91
i=3	-1,038	-1,5	0,07	0,6	-1,2
i=4	1,779	1,563	-0,27	-0,4	1,36
i=5	0,01	-0,25	0,07	1,6	-0,18

Źródło: opracowanie własne

Unitaryzacja polega na zastosowaniu następującej formuły:

7.9.

gdzie: z_ij - wartość i-tej obserwacji j-tej cechy po unitaryzacji, min x_ij - najmniejsza wartość cechy x_j (i=1,...n), R_j - rozstęp cechy x_j. Po unitaryzacji wartość wszystkich cech są niemianowane i zawarte w przedziale od 0 do 1 czyli [0,1].

Przykład 7.3. Procedura unitaryzacji danych. Etap pierwszy polega na wyznaczeniu minimalnych wartości poszczególnych cech oraz obliczeniu obszaru zmienności cech zgodnie z formułą 3.23.

	j=1	j=2	j=3	j=4	j=5
min xj	0,702	0,63	1,2	3,1	1,2
Rj	0,293	0,49	0,4	0,3	3,5

Źródło: opracowanie własne na podstawie tabeli 7.2.

Etap drugi polega na obliczeniu wartości zunitaryzowanych z_ij macierzy Z. Korzystamy z formuły 7.9. Wartości zunitaryzowane cechy pierwszej:

z₁₁ =
= 0,42

z₂₁ =
= 0,06

z₃₁ =
= 0

z₄₁ =
= 1

z₅₁ =
= 0,37

Wartości zunitaryzowane cechy drugiej:

z₁₂ =
= 0,76

z₂₂ =
= 0,67

z₃₂ =
= 0

z₄₂ =
= 1

z₅₂ =
= 0,41

Podobne obliczenia wykonujemy w przypadku pozostałych wartości cech dla obiektów. Etap trzeci polega na budowie macierzy znormalizowanej Z.

i j	j=1	j=2	j=3	j=4	j=5
i=1	0,42	0,76	0	0	0,83
i=2	0,06	0,67	1	0,33	0,11
i=3	0	0	0,5	0,67	0
i=4	1	1	0,25	0,33	1
i=5	0,37	0,41	0,5	1	0,4

Źródło: opracowanie własne

Klasyfikacja może doprowadzić do podziału zbioru n obiektów na K rozłącznych i niepustych podzbiorów zwanych klasami w ten sposób, aby wewnątrz danej klasy znalazły się obiekty najbardziej podobne do siebie, natomiast do różnych klas elementy mało podobne.

Operacja standaryzowania i unitaryzowania pozwala na obliczenie odległości pomiędzy danym elementem a pozostałymi elementami zbioru. Można w tym celu wykorzystać kilka metod liczenia odległości:

- jako przeciętnej bezwzględnych różnic cech;

- jako pierwiastka z przeciętnej kwadratów różnic cech;

- jako sumę bezwzględnych różnic cech;

- jako pierwiastka z sumy kwadratów różnic cech.

Obliczenie odległości przy wykorzystaniu z jednej z powyższych metod jest równoznaczne z określeniem macierzy odległości. Macierz tę można zapisać w postaci:

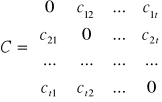
7.10.

gdzie: c_ij - odległość obiektu i-tego od j-tego.

Elementy macierzy odległości stanowią podstawę dla wszelkich zagadnień taksonomicznych. Posiadają one kilka podstawowych własności, takich jak: c_rr = 0, co oznacza, że odległość obiektu r-tego od samego siebie wynosi zero; c_rs = c_sr, co oznacza, ze odległość między obiektem r-tym a s-tym jest równa odległości między obiektem s-tym i r-tym oraz c_rs ≤ c_rp + c_ps , co oznacza, że odległość między r-tym i s-tym obiektem jest mniejsza lub równa sumie odległości między obiektem r-tym i p-tym oraz p-tym i s-tym.

7.4. Taksonomiczne mierniki rozwoju

Metody porządkowania liniowego stosowane w miernikach rozwoju różnią się od metod klasyfikacji. Można je bowiem stosować, gdy wszystkie zmienne charakteryzujące zjawisko są stymulantami lub destymulantami. Stymulanta to zmienna, której wzrost świadczy o wzroście poziomu zjawiska złożonego. Destymulanta opisuje sytuację odwrotną. Nominanty mogą natomiast przyjmować charakter tak jednych, jak i drugich. Celem stosowania metody porządkowania liniowego jest uporządkowanie obserwacji, od najlepszej do najgorszej. Kryterium uporządkowania jest poziom zjawiska złożonego.

Jedną z metod porządkowania liniowego jest metoda wzorca rozwoju. Postępowanie jest trzyetapowe. Najpierw wyznacza się wzorzec rozwoju Z₀, o najlepszych wartościach dla każdej zmiennej

Z₀ = [Z₀₁, Z₀₂, ..., Z_0m] 7.11.

gdzie:

z_0j =
Z_ij , gdy zmienna Z_j jest stymulantą

oraz

z_0j =
Z_ij , gdy zmienna Z_j jest destymulantą

oraz antywzorzec Z_-0 dla najgorszych wartości każdej zmiennej

Z_-0 = [Z_-01, Z_-02, ..., Z_-0m] 7.12.

gdzie:

z_-0j =
Z_ij , gdy zmienna Z_j jest destymulantą

oraz

z_-0j =
Z_ij , gdy zmienna Z_j jest stymulantą

W drugim etapie badane jest podobieństwo między danym obiektem a wzorcem poprzez obliczenie odległości

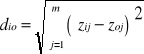
7.13.

dla i = 1, ..., n.

Im obiekt jest położony bliżej wzorca, tym wyższy poziom zjawiska złożonego, który on reprezentuje.

W etapie trzecim wyznaczamy miarę rozwoju dla każdego obiektu według formuły:

7.14.

dla i = 1, ..., n.

gdzie: d₀ - odległość między wzorcem rozwoju a antywzorcem, liczona według formuły:

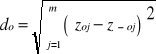
7.15.

Miara rozwoju jest tym wyższa, im obiekt reprezentuje wyższy poziom zjawiska złożonego. Wartość miary rozwoju jest unormowana i mieści się w przedziale [0,1]. Dla wzorca rozwoju miara ta wynosi 1, dla antywzorca 0.

Przykład 7.4. W przykładzie wykorzystano dane zamieszczone w macierzy obserwacji 7.2. Na podstawie tej macierzy dokonano identyfikacji charakteru poszczególnych cech, rozróżniając stymulanty, destymulanty i nominanty. Te ostatnie muszą być przypisane w zależności od sytuacji do jednej z dwóch pierwszych grup. Na tej podstawie tworzy się macierz zestandaryzowaną.

i j	j=1	j=2	j=3	j=4	j=5
i=1	0,144	0,313	-0,6	-1,4	0,92
i=2	-0,885	-0,125	0,73	-0,4	-0,91
i=3	-1,038	-1,5	0,07	0,6	-1,2
i=4	1,779	1,563	-0,27	-0,4	1,36
i=5	0,01	-0,25	0,07	1,6	-0,18

Źródło: opracowanie własne

W etapie drugim budowany jest wzorzec Z_o i antywzorzec Z_-o, zgodnie z formułami 7.11 oraz 7.12. Mają one postać:

Z_o = [1,779; 1,563; -1,385; 1,6; 1,36] oraz Z_-o = [-1,038; -1,5; 1,692; -1,4; -1,2]

Jedną destymulantą jest liczba osób na 1 izbę mieszkalną, natomiast cztery pozostałe to stymulanty. W etapie czwartym bada się podobieństwo między danym obiektem a wzorcem poprzez obliczanie odległości według formuły 7.13. Otrzymano wyniki:

d₁₀ =
= 3,665

d₂₀ =
= 5,345

d₃₀ =
= 5,219

d₄₀ =
= 2,173

d₅₀ =
= 3,34

W etapie czwartym wyznaczane są normy rozwoju dla każdego obiektu według formuły 7.14. przy wykorzystaniu formuły 7.15.

d_o =
= 6,507

Otrzymano wyniki:

m₁ =
= 0,437

m₂ =
= 0,179

m₃ =
= 0,198

m₄ =
= 0,671

m₅ =
= 0,487

Obiektem położonym najbliżej wzorca jest obiekt numer 4 czyli gmina Świdnica. Podobna procedura może zostać przeprowadzona w oparciu o zmienne zunitaryzowane. Wykorzystujemy macierz zunitaryzowaną

i j	J=1	j=2	j=3	j=4	j=5
i=1	0,42	0,76	0	0	0,83
i=2	0,06	0,67	1	0,33	0,11
i=3	0	0	0,5	0,67	0
i=4	1	1	0,25	0,33	1
i=5	0,37	0,41	0,5	1	0,4

Źródło: opracowanie własne

Wyznaczamy wzorzec Z_o i antywzorzec Z_-o. Otrzymujemy wyniki: Z_o = [1;1;0;1;1] oraz Z_-o = [0;0;1;0;0]. W kolejnym etapie obliczamy odległości zgodnie z formułą 7.13. Otrzymujemy wyniki:

d₁₀ =
= 1,19

d₂₀ =
= 1,80

d₃₀ =
= 1,83

d₄₀ =
= 0,72

d₅₀ =
= 1,16

W etapie czwartym wyznaczane są normy rozwoju dla każdego obiektu według formuły 7.14. przy wykorzystaniu formuły 7.15.

d_o =
= 2,24

Otrzymano wyniki:

m₁ =
= 0,47

m₂ =
= 0,20

m₃ =
= 0,18

m₄ =
= 0,68

m₅ =
= 0,48

Obiektem położonym najbliżej wzorca jest obiekt numer 4 czyli gmina Świdnica.

Zadania i pytania

7.1. Obliczyć miarę rozwoju społecznego miast

Cecha - Miasto	Wałbrzych	Nowa Ruda	Boguszów-Gorce	Świdnica	Kłodzko
Liczba osób na lekarza	22	28	26	19	21
Liczba osób na mieszkanie	5	6	5	6	5
Liczba uczniów na nauczyciela	27	24	22	22	26
Liczba gazet na osobę rocznie	11	9	10	15	9
Liczba przestępstw na osobę	0,8	1,2	1,0	1,1	1,4

7.2. Obliczyć miarę czystości ekologicznej gminy

Cecha - Gmina	Żarów	Jaworzyna	Strzegom	Jawor	Dobromierz
Emisja SO2 w kg/osobę	40	25	19	16	17
Czystość wód w %	11	13	14	12	11
Ilość odpadów na osobę w kg	22	25	29	31	25
Liczba oczyszczalni ścieków	8	7	6	4	7
Nakłady na ochronę środowiska w tys. zł/osobę	2,34	2,43	2,18	2,33	2,36

7.3. Obliczyć miarę rozwoju rolnictwa w gminie

Cecha-Gmina	Świdnica	Jaworzyna	Marcinowice	Strzegom	Dobromierz
Użytki rolne na osobę w ha	0,96	0,77	0,95	0,93	0,98
Liczba bydła na ha ziemi	2,45	2,75	2,85	2,76	2,88
Nawozy na ha ziemi w kg	54	57	59	58	62
Liczba traktorów na ha ziemi	1,24	1,34	1,53	1,49	1,76
Plony zbóż w kwintalach z ha	35	38	39	35	31
Liczba osób na gospodarstwo	1,23	1,89	1,77	1,84	1,22

W.S.Jevons, Principles of Science, London 1874.

Ten sposób klasyfikacji zagadnień, w których maja zastosowanie metody taksonomiczne zaproponowali autorzy monografii wydanej w 1988 roku. Por.: J.Pociecha, B.Podolec, A.Sokołowski, K.Zając, Metody taksonomiczne w badaniach społeczno-ekonomicznych, Warszawa 1988, s. 23-32.

J.Pociecha i inni, Metody ..., op.cit., Warszawa 1988.

Taksonomiczna analiza przestrzennego zróżnicowania poziomu życia w Polsce w ujęciu dynamicznym, red. A.Zeliaś, Kraków 2000.

J.Pociecha i inni, Metody ..., op.cit., Warszawa 1988.

Szerzej na ten temat: T.Borys, Kategoria jakości w statystycznej analizie porównawczej (w) Prace Naukowe AE we Wrocławiu, nr 284/1984, seria „Monografie i Opracowania” nr 23, 1984.

E.Nowak, Metody taksonomiczne w klasyfikacji obiektów społeczno-gospodarczych, Warszawa 1990, s. 14.

E.Nowak, Metody taksonomiczne w klasyfikacji obiektów społeczno-gospodarczych, Warszawa 1990, s. 16.

Szerzej problemy tego typu przedstawia E.Nowak w pracy: „Metody taksonomiczne w klasyfikacji obiektów społeczno gospodarczych”, w rozdziale czwartym.

Florek K., Łukaszewicz J., Perkal J., Steinhaus H., Zubrzycki S., Taksonomia wrocławska (w) „Przegląd Antropologiczny”, 1951, t. XVII.

171

---