1. Ogólne założenia teorii kinetyczno - molekularnej.

a)ciała mają budowę nieciągłą i składają się z drobnych elementów w postaci stanów lub cząsteczek

b)wymienione elementy budowy ciał są w ciągłym ruchu wartości liczbowe i kierunki prędkości poszczegulnych elementów są różne

c)pomiędzy poszczegulnymi elementami budowy ciała występują siły wzajemnego oddziaływania, które w dużym stopniu zależą od odległości między cząsteczkami.Z punktu widzenia tych odległości ciała stałe i ciecze traktujemy jako jedną grupę.

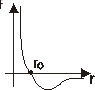
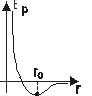
Z wykresu sił widać że dla pewnej odległości r siła równa się 0⇒ stan równowagi trwałej układu

Tej samej odległości odpowiada min E_p co jest właśnie warunkiem trwałości równowagi.

dla r>r₀ - siły przyciągania, dla r <r₀ - siły odpychania

2. Rozkład prędkości Maxwella. Wyprowadzić wzór barometryczny.

∗ Kierunek cząsteczek gazowych jest chaotyczny i bezładny.

∗ Wartość prędkości nie jest przypadkowa

Prawo rozkładu prędkości Maxwella zostało wyprowadzone w oparciu o następujące założenia:

- zderzenia cząsteczek mają charakter doskonale sprężysty

- liczba cząsteczek dN mających prędkości zawarte w granicach od V do V+dV jest stała

Niech dN oznacza liczbę cząsteczek w prędkościach zawartych w granicach <V, V+dV>. Na skutek nie uniknionych zderzeń pewna liczba cząsteczek zmienia swą prędkość, a więc przechodzi do innego przedziału. Na ich miejsce w tym samym czasie wchodzi taka sama liczba cząsteczek, które poprzednio miały prędkości leżące poza granicami <V,V+dV>.Jest to słuszne tylko wtedy, gdy liczba cząsteczek dN jest bardzo dużą.

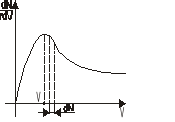
Pole prostokąta wyraża liczbę cząsteczek o ν∈<V,V+dV>. Stopniowo przesuwając się od prędkości najmniejszej do największej można by podzielić pole pod krzywą na nieskończenie wiele prostokątów. Więc pole pod krzywą przedstawiałoby liczbę cząsteczek Ng_czo. Z istnienia max krzywej wiemy, że pewnej określonej wartości prędkości odpowiada największa liczba cząsteczek.

Z asymetrii krzywej względem osi pionowej wnioskujemy, że prędkość średnia

dN- liczba cząsteczek w przedziale prędkości V i V+dV

V - ogólna liczba cząsteczek

3. Wyprowadzić wzór na ciśnienie gazu doskonałego.

Wstępne założenia:

1)gaz jest zawarty w naczyniu kulistym o promieniu r

2)gaz jest tak rozrzedzony, że można brać pod uwagę tylko zderzenia ze ściankami naczynia zaniedbując zderzenia międzycząsteczkowe

Obliczenie średniego ciśnienia p działającego na powierzchnię S wymaga znajomości siły F działającej na powierzchnię. Z drugiej zasady dynamiki wiadomo że:

Badana cząstka zachowuje się jak kulka doskonale sprężysta. Na podstawie prawa mówiącego że kąt padania równy jest kątowui odbicia. Tesame kąty padania i odbicia istnieją po zderzeniach ze ścianko naczynia.

Z prawa odbicia wynika także że kolejne punkty odbicia leżą w jednej płaszczyźnie. Punkty zmieniałyby płaszczyzny jeżeli zachodziłoby dzerzanie między cząsteczkowe.

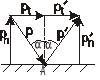
Obliczenie siły F można zatem sprowadzić do wyznaczania zmiany pędu pojedyńczej cząsteczki przy jednym jej zderzeniu ze ścianko naczynia.

Pdczas zderzenia składowa styczna nie ulega zmianie natomiast składowa normalna zmienia swój znak na przeciwny. A zatem zmiana pędu powstająca podczas odbicia równa się róznicy wartości liczbowych składowych normalnych pędu przed i po odbiciu

mVcosα-(-mVcosα)=2mVcosα

chcąc określić całkowitą siłę działającą na ściankie naczynia pochodzącą od jednej cząsteczki musimy obliczyć zmiane jej pędu w czasie 1s. Do tego potrzebna jest znajomość liczby n uderzeń cząsteczki o ścianke w czasie 1s

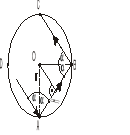
Zmiana pędu odpowiada n uderzeniom (w czasie 1s) będąca miarą siły oddziaływania 1 cząsteczki na ściankę naczynia wyraża się wzorem: f=2mVcos αn+2mVcos α*V/2rcos2mVcos α f=mV²/r

W naczyniu mamy nie jedną ale N cząsteczek o jednakowych masach jeżeli gaz jest jednorodny o różnych prędkościach V₁ V₂ V₃... V_N. Całkowita siła działająca na powierznie wewnętrzną naczynia, poczhodząca od wszystkich cząsteczek

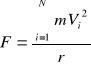
Pamiętając że ciśnienie
, a S=4Πr² znajdujemy:

4. Omówić zasadę ekwipartycji energii.

Zasada ta mówi orównomiernym podziale średniej E_k w ilości 0,5kT gdzie: k - stała Boltzmana, T - temperatura bezwzględna.

Rozważmy to dla jednoatomowej cząsteczki poruszającej się z prędkością V. Cząsteczka ta ma trzy stopnie swobody. Ujmując zależności wektorów

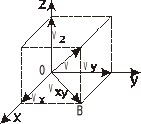
OB=V_x+V_y

Przy dostatecznie dużej liczbie cząsteczek biorących udział w ruchu cieplnym można ten ruch uważać za chaotyczny. Czyli nie może występować przewaga jakiejkolwiek z 3 E_x

E_x=E_y=E_z=1/3E_k Ponieważ średnia E_k ruchu postępowegocząstki jednoatomowej 1/3E_k=1/2kT E_x =3/2kT

Możemy przez połowe pojedyńczej masy cząsteczki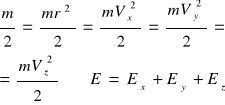

5. Podać pierwszą zasadę termodynamiki i definicję wielkości w niej występujących. Wyprowadzić wzór definjujący temp. bezwzględną i podać jej interpretację.

I zasada termodynamiki:

Aby zmienić energię wewnętrzną ciała należy dostarczyć mu ciepła lub wykonać nad nim pracę ΔU=ΔQ+ΔW

Ciepło i praca charakteryzują przemianę jakiej podlega układ. Przyrost ΔU nie zależy od rodzaju przemiany. Temperatura jest miarą średniej energii kinetycznej cząsteczek. Jednostką temp. w układzie Si jest Kelwin [K].

Ciepło forma przekazania energii układowi termodynamicznemu. Jednostką jest Dżul. Praca skalarna wielkość fizyczna określająca wartość energii wydatkowanej na przemieszczenie ciała materialnego z położenia początkowego do końcowego W=F*s. Ciepło właściwe ilość ciepła pobranego przez jednostkę danego układu powodująca wzrost temp. układu o 1^oK. Temp.bezwzględna (T) wielkość charakteryzująca stan równowagi termodynamicznej. Definjowana jest jako odwrotność pochodnej eutrapi E:

Jest miarą średniej e. kinetycznej cząsteczek. Entrapia funkcja stansu

We wszystkich procesach idealnie odwracalnych entrapia jest stała. W rzeczywistych entrapia zawsze rośnie>

6.Omów przemianę izochoryczną i izobaryczną. Wyprowadź r-nie Meyera C_p=C_v+R.

Przez izoprzemianę rozumiemy taką przemianę przy której jeden z parametrów charakteryzujących stan ciała pozostaje stały. Przemiana izochoryczna- dV=0 (zmiana objętości), a zatem dW=0 (zmiana pracy). Z I zasady termodynamiki otrzymujemy dQ=dV (zmiana ciepła dostarczonego ciału = zmianie energii wewnętrznej ciała) Doprowadzenie ciepła do ciała przy niezmiennej objętości powoduje wzrost jego energii wewnętrznej równy dostarczonej energii cieplnej. Przemiana izobaryczna - przemiana zachodząca przy stałym ciśnieniu. Ogrzewany 1 mol gazu doskonałego o dT pod stałym ciśnieniem. Ilość ciepła pobranego dQ=C_pdT gdzie: C_p- ciepło molowe pod stałym ciśnieniem. Przyrost energii wewnętrznej podczas ogrzania o dT wynosi dV= C_vdT. Gaz zwiększa swą objętość o dVm, a więc praca wykonana dW=pdV_m. Z I zasady termodynamiki wynika zatem, że CpdT=C_vdT+pdV_m. Ale pV_m=RT, stąd jeśli p=const, to pdV_m=RdT. Po podstawieniu CpdT= C_vdT+RdT czyli: Cp=C_v+R

7. Omówić przemianę izotermiczną i izochoryczną.

Przemiana izotermiczna- ponieważ w przypadku gazu doskonałego energia wewnętrzna jest tylko funkcja temp. nie zależy od objętości i ciśnienia. Ponieważ w przemianie izotermicznej T=const więc U₁=U₂ czyli dV=0. Stąd wniosek, że w elementarnej przemianie izotermicznej gazu doskonałego ciepło zmienia się całkowicie na pracę (lub odwrotnie) dQ=dW.

8.Omów przemianę adiabatyczną wyprowadź równanie przemiany.

Przemiana adiabatyczna - przemiana podczas której nie ma wymiany ciepła z otoczeniem. Ponieważ w przemianie adiabatycznej dQ=0 więc dV= - dW

Rozważmy adiabatyczne rozprężenie się jednego mola gazu doskonałego. W tej przemianie dW=+pdVm - praca zostaje wykonana kosztem energii wewnętrznej o dV=C_vdT. A zatem C_vdT= - pdVm, pdVm= RT Podczas tej przemiany ciśnienie ulega zmianie

⇒ po scałkowaniu ⇒ *

*
,

ale: R=C_p-C_V, a zatem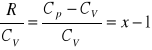

gdzie: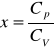

Równanie przyjmuje postać
Mnożąc je stronami przez pV_m=RT otrzymujemy

skąd
⇒

9. Omów II zasadę termodynamiki w oparciu o statyczną definicję entropii.

Silnik termodynamiczny - urządzenie zasilane energią cieplną, pracujące w zamkniętych obiegach i dostarczające prace w każdym obiegu bez zużywania się ciała roboczego, czyli czynnika termodynamicznego.

II zasada termodynamiki określa możliwość przemiany ciepła na pracę czyli innymi słowy podaje warunki [pracy silnika termodynamicznego.

III Zasada termodynamiki - zmiana ciepła na pracę w silniku termodynamicznym jest możliwa jedynie wtedy, gdy źródło dostarczające ciepło ma temperature wyższą od najziomniejszego ciała w jego otoczeniu.

Entropia - termodynamiczna skalarna funkcja stanu
gdzie: dQ - ciepło pobrane przez układ w temp. bezwzględnej T Entropia określona jest z dokładnością do stałej. We wszystkich procesach idealnie odwracalnych entropia jest stała. W rzeczywistych procesach entropia całego układu zawsze rośnie.

W oparciu o statyczną definicję entrapii. Istnieje entrapia będąca funkcją stanu układu, stałą w odwracalnych procesach adiabatycznych i rosnącą we wszystkich innych. Zasadę tę zgodnie z którą kierunek wzrostu entrapii może służyć do formalnego wyróżnienia kierunku upływu czasu (wszystkie inne prawa fizyki klasycznej nie ulegają zmianie przyszłości z przeszłością).

-równanie obowiązujące w przemianach kołowych odwracalnych

Podczas przejścia odwracalnego 1→a→2 suma ilości ciepła zredukowanego:
zmieniło się o pewną wartość. Zmianę tę oznaczono ΔS. Zmiana ciepła zredukowanego podczas przejścia odwracalnego
ma przeciwny znak, lecz wartość tę samą.

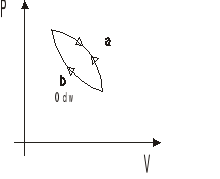
Łączne ciepło zredukowane odpowiadające przejściu odwracalnemu od stanu 1 do 2 nie zależy od rodzaju przemiany, a zależy od stanu początkowego i końcowego.

10. Omówić gazy rzeczywiste, równanie Van der Waalsa.

*Gazy nie mają podobnie jak ciecze sprężystości postaciowej G=0 nie mają swobodnej powierzchni, lecz wypełniają całkowite zajmowane naczynie.

*Mają cechę rozprężliwości tzn. dążą do zajęcia jak największej objętości.

*Ciśnienie w gazie sywającym rozchodzi się we wszystkich kierunkach jednakowo

Równanie stanu gazów rzeczywistych (równanie Van der Walsa)

gdzie:a,b-stałe charakterystyczne dla gazu, które wyznaczane są empirystycznie na podstawie zależności.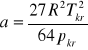

gdzie: T_kr,p_kr-temp. i ciśnienie gazu w stanie krytycznym, V - objętość gazu, n - liczba moli gazu, R - stała gazowa, T - temp. bezwzględna

11. Omów różnicę między gazem i parą.

Gaz - stan lotny substancji powyżej temp. krytycznej kiedy to nawet przy bardzo dużym ciśnieniu nie udaje się go skroplić (jeden ze stanów skupienia materii)

Para - stan lotny substancji, jednak w odpowiednich warunkach może nastąpić kondensacja i przejście w ciecz. W temp. większej od krytycznej substancja zachowuje się tak jak gaz doskonały.

W temp. nie znacznie wyższej od temp krytycznej gaz wykazuje odstępstwa od równania Clapeyrona ale nie można go skroplić.

12. Omów zjawisko dyfuzji i przewodnictwa cieplnego w gazach.

Dyfuzja gazów - wzajemne przenikanie się gazów w wyniku przemieszczenia się cząsteczek jednego gazu popomiędzy cząsteczkami drugiego. Dyfuzja zawsze sprowadza się do transportu masy z obszaru o większym do obszaru o mniejszym stężeniu. W przypadku stykających się gazów występuje zawsze, jeśli tylko gazy nie zachodzą ze sobą w gwałtowną reakcję chemiczną.

Gdyby cząsteczki gazów poruszały się bez zderzeń, proces dyfuzji zachodziłby bardzo szybko. Pomimo, iż cząsteczka w ciągu sekundy przebiega drogę kilkuset metrów, to po tym czasie jej położenie nieznacznie się zmienia. Im więcej zderzeń tym wolniej przebiega dyfuzja.

Przewodnictwo cieplne w gazach - polega na przekazaniu E_k bezwładnego ruchu cieplnego od jednych cząsteczek do drugich w skutek zderzeń. Różnica temp. w różnych obszarach wiąże się z istnieniem różnic średnich E_k cząsteczek w tych obszarach. Ale w skutek nieuniknionych zderzeń cząsteczek stopniowo wyrównuje się E_k i T.

Przewodnictwo cieplne w gazach zależy od ciśnienia.

13. Zjawisko lepkości w gazach i cieczach.

Lepkość - cecha płynów, pojawianie się siły tarcia pomiędzy warstwami cieczy lub gazu, poruszającymi się równolegle względem siebie z różnymi co do wartości prędkościami. Warstwa poruszająca się szybciej działa przyspieszająco na warstwę poruszającą się wolniej i oodwrotnie. Pojawiające się wtedy siły tarcia wewnętrznego skierowane są stycznie do powierzchni styku tych warstw. Newton wykazał że siła ta wyraża się wzorem

η - wsp. Lepkości charakterystyczny dla danego ośrodka, ΔV - różnica prędkości obu warstw, czyli prędkość względna jednej warstwy względem drugiej.

14. Omów zjawisko napięcia powierzchniowego.

Na molekuły znajdujące się na powierzchni cieczy działają sąsiednie molekuły położone na powierzchni i tuż pod niąOprócz tego na molekuły powierzchniowej warstwy cieczy działają siły F leżące w płaszczyźnie stycznej do powierzchni cieczy. Dla każdej z molekuł leżących wewnątrz powierzchni wszystkie te siły wzajemnie się równoważą. Jednakże dla molekuł położonych na obwodzie powierzchni siły F skierowane na zewnątrz są siłami

zewnętrznymi i są prostopadłe do obwodu i styczne do powierzchni cieczy. Te zewnętrzne siły w warstewce powierzchniowej nazywamy siłami napięcia powierzchniowego.

Liczbowa wartość długości obwodu nazywa się wsp. nap. pow. danej cieczy. Oznaczając długość obwodu powierzchni S przez L znajdziemy wartość bezwzględną wszystkich sił

zewnętrznych F_i działających na molekułę przez F otrzymamy współ. napięcia powierzchniowego α=F/L.

15. Omów zjawisko włoskowatości.

Włoskowatością nazywamy zjawisko obserwowane w cienkich kapilarach. Zanurzając częściowo kapilarę w cieczy zwilżającej obserwujemy, że poziom cieczy w kapilarze jest wyższy niż poziom cieczy poza kapilarą, a powierzchnia swobodna w kapilarze jest wklęsła. Zanurzając kapilarę w cieczy nie zwilżającej obserwujemy, że poziom cieczy w kapilarze jest niższy niż poza kapilara a powierzchnia swobodna cieczy w kapilarze jest wypukła. Zmianom wysokości słupka cieczy w kapilarze towarzyszą zmiany powierzchni styku cieczy z wew. powierzchnią kapilary, a tym samym zmiany energii przylegania. Jeżeli ciecz ma względem tej powierzchni własności zbliżające to będzie dążyć do zwiększenia powierzchni styku.

---