1. Wprowadzenie

Materiały przewodzące, jak na przykład metale, czy półprzewodniki, których nośniki ładunku mają różną od zera prędkość dryfu V, wykazują, w zewnętrznym polu magnetycznym, tzw. efekt Halla. Polega on na powstawaniu pola elektrycznego E_H o kierunku poprzecznym do kierunku natężenia prądu I płynącego w próbce , jeśli badana próbka zostanie umieszczona w polu magnetycznym o indukcji B prostopadłej do kierunku I. Wynikiem powstałego, poprzecznego pola elektrycznego jest poprzeczny do kierunku przewodzenia spadek potencjału, dający tak zwane napięcie Halla U_H.

Rys.1. Efekt Halla w przewodzącej płaskorównoległej próbce

2. Cel ćwiczenia

Celem ćwiczenia jest:

- ustalenie prawidłowości rządzących efektem Halla, wyznaczenie stałej Halla,

- wyznaczenie koncentracji i ruchliwości nośników prądu w germanie ( typu p lub n ),

- wyciągnięcie wniosków dotyczących rodzaju przewodnictwa w badanej próbce,

Cel ten osiągniemy analizując zależność napięcia Halla U_H od natężenia prądu I przepływającego przez próbkę, gdy jest ona umieszczona w stałym polu magnetycznym o indukcji B , lub zależność napięcia Halla UH od wielkości indukcji B pola magnetycznego, gdy przez próbkę przepływa prąd o stałym natężeniu I.

3. Metoda pomiaru i układ pomiarowy

Ideowy schemat metody pomiarowej przedstawiono na rysunku 1, gdzie pomiarów

napięcia Halla U_H dokonuje się w poprzek próbki, między punktami D i G.

Aparatura do pomiaru efektu Halla stosowana w tym doświadczeniu ( rys.2 ) zawiera:

- obwód zasilania badanej próbki ( zasilacz I )

- mierniki:

a) natężenia prądu I sterującego próbka (cyfrowy miliamperomierz w Module II )

b) napięcia Halla U_H ( cyfrowy miliwoltomierz VI ).

- elektromagnes ( III )

- sondę do pomiaru indukcji B ( Hallotron V )

- miernik indukcji pola magnetycznego ( Teslametr IV ).

Rys.2. Układ pomiarowy stosowany do analizy efektu Halla i pomiaru magnetooporu.

4. Przebieg pomiaru.

a) Pomiar U_H = f(I)

B [T]	200 mT
I [A]	-0,04	-0,035	-0,03	-0,025	-0,02	-0,015	-0,01	-0,005	0
UH [V]	0,0942	0,0868	0,0764	0,0626	0,0514	0,0376	0,0267	0,0145	0,0046
I [A]	0,005	0,01	0,015	0,02	0,025	0,03	0,035	0,04
UH [V]	-0,0102	-0,023	-0,0347	-0,0468	-0,0576	-0,0703	-0,0804	-0,0914

B [T]	240 mT
I [A]	-0,04	-0,035	-0,03	-0,025	-0,02	-0,015	-0,01	-0,005	0
UH [V]	0,1158	0,1004	0,0859	0,0728	0,0577	0,0447	0,032	0,0179	0,0054
I [A]	0,005	0,01	0,015	0,02	0,025	0,03	0,035	0,04
UH [V]	-0,0125	-0,0245	-0,0408	-0,055	-0,0666	-0,0789	-0,0936	-0,1057

Jak można zaobserwować na wykresie w pierwszym jak i drugim przypadku U_H zależy liniowo od I.

Współczynniki kierunkowe prostych:

a) a = -2,387353
z Δa = 0,015867
dla B = 200 mT

b) a = -2,777696
z Δa = 0,014629
dla B = 240 mT

Wartość stałej Halla, przy ustalonej indukcji B, dla:

R_H = aS / Bd,

d = 0,001 m,

S = 0,00001 m²

a) B = 200 mT,

a = -2,387353

R_H = (-0,1194 ± 0,0008)

2. B = 240 mT,

a = -2,777969

R_H = (-0,1158 ± 0,0006)

Badana próbka jest koncentracją elektronów n (tzn. liczbą elektronów w jednostce objętości) ponieważ wskazuje na to znak „-” przy stałej Halla. Wielkość stałej Halla jest zależna od indukcji pola magnetycznego ale w małym stopniu, co widać w wynikach stałej Halla dla dwu różnych wartości B.

Szacunkowa wartość błędu ΔR_H.

∆R_H = ∆aS/(Bd), gdzie: ∆a - błąd pomiaru współczynnika kierunkowego

S - pole przekroju próbki

B - indukcja magnetyczna

d - szerokość próbki

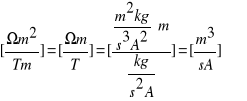
B [T]	ΔRH [ ]
200 mT	0,0008
240 mT	0,0006

b) Pomiar U_H = f(B)

I [A]	20 mA
B [T]	-0,001	0,007	0,057	0,108	0,160	0,205	0,248
UH [V]	-0,0107	-0,0122	-0,0208	-0,0295	-0,0385	-0,0461	0,0533

I [A]	-20 mA
B [T]	-0,001	0,008	0,05	0,105	0,163	0,207	0,250
UH [V]	0,0107	0,0125	0,0208	0,0315	0,0427	0,0511	0,0593

Jak można zaobserwować na wykresie w pierwszym jak i drugim przypadku U_H zależy liniowo od B.

Współczynniki kierunkowe prostych:

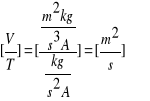
a) a = -0,1711321
z Δa = 0,0004323
dla I = 20 mA

b) a = 0,1936752
z Δa = 0,0005327
dla I = -20 mA

Wartość stałej Halla, przy ustalonym prądzie I, dla:

R_H = aS / Id,

d = 0,001 m,

S = 0,00001 m²

a) I = 20 mA,

a = -0,1711321

R_H = (-0,0856 ± 0,0002)

3. I = -20 mA,

a = 0,1936752

R_H = (-0,0968 ± 0,0003)

Badana próbka jest koncentracją elektronów n (tzn. liczbą elektronów w jednostce objętości) ponieważ wskazuje na to znak „-” przy stałej Halla. Wielkość stałej Halla jest zależna od wielkości prądu I sterującego próbką. W jednym tylko przypadku wartości stałej Halla R_H są podobne, gdy wielkości prądu sterującego próbką są przeciwnych znaków, jak widać to w obliczeniach.

Szacunkowa wartość błędu ΔR_H.

∆R_H = ∆aS/(Id), gdzie: ∆a - błąd pomiaru współczynnika kierunkowego

S - pole przekroju próbki

I - natężenie prądu płynącego przez próbkę

d - szerokość próbki

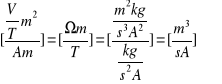
I [A]	ΔRH [ ]
20 mA	0,0002
-20 mA	0,0003

4. Obliczanie koncentracji i ruchliwości nośników prądu.

• obliczenie koncentracji

e = 1.61 x 10^-19 C

n = -1 / R_H · e

dla	RH [ ]	n [1/m^3]
B = 200 mT	-0,11938	5,202865 x 10^-19 C
B = 240 mT	-0,11575	5,36603 x 10^-19 C
I = 20 mA	-0,08557	7,258595 x 10^-19 C
I = -20 mA	-0,09684	6,413858 x 10^-19 C

• obliczenie ruchliwości

μ = σ / n · e, gdzie σ = l / R₀ · S - przewodnictwo próbki,

l = 0,02 m - długość próbki

R₀ = 53 Ω,

S = 0,00001 m²

σ = 37,73585 [1/Ωm]

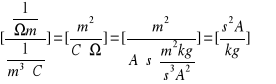
dla	n [1/m^3]	μ [ ]
B = 200 mT	5,202865 x 10^-19 C	4,50490558 x 10^-19 C
B = 240 mT	5,36603 x 10^-19 C	4,36792481 x 10^-19 C
I = 20 mA	7,258595 x 10^-19 C	3,2290568 x 10^-19 C
I = -20 mA	6,413858 x 10^-19 C	3,65433964 x 10^-19 C

Wartości obliczonej przez nas stałej Halla oraz koncentracji nośników ładunków różnią się od wartości tablicowych. Może to być spowodowane tym, że w tablicach podana jest wartość dla germanu w stanie możliwie czystym nastomiast badana przez nas próbka mogła posiadać zanieczyszczenia, które wpłynęły na rozbieżność wyników. Także temperatura, w której był dokonywany pomiar mogła mieć niewielki wpływ na wynik różniący się od wartości tablicowych (w tabeli jest podana koncentracja nośników ładunków dla germanu w temperaturze pokojowej). Także inne doświadczenia wykonywane przez pozostałe grupy mogły wywrzeć nieznaczny wpływ na wyniki pomiarów (np. doświadczenie z wykorzystaniem promieniowania β). Wyniki pomiarów mogły być też uwarunkowane niedokładnością przyrządów pomiarowych.

1. Wnioski

Z analizy wykresu U (I) wynika, że natężenie jest rosnącą liniową funkcją napięcia. Zauważamy, że zmiany indukcji magnetycznej wywierają silny wpływ na wartość stałej Halla - wzrost indukcji powoduje zmniejszenie stałej Halla. Z analizy wykresu U (B) wynika, że natężenie jest rosnącą liniową funkcją napięcia. Zauważamy, że zmiany natężenia wywierają mniejszy wpływ na wartość stałej Halla niż zmiany indukcji magnetycznej - wzrost natężenia powoduje niewielkie zmniejszenie stałej Halla. Jeśli chcemy zakrzywić tor ruchu nośników ładunku w wyniku działania siły Lorentza, to lepiej jest zwiększyć indukcję pola magnatycznego niż zwiększyć natężenie płynącego przez materiał prądu (zwiększenie indukcji powoduje dużo większy wzrost stałej Halla niż zwiększenie natężenia płynącego prądu). Ujemne wartości stałej Halla zarówno w części a) ćwiczenia (przy stałej indukcji pola magnetycznego), jak i w części b) ćwiczenia (przy stałym natężeniu prądu) potwierdzają fakt, że nośnikami prądu w germanie były w tym przypadku elektrony, a więc mieliśmy do czynienia z przewodnictwem typu n - german jest więc metalem. Obliczona wartość stałej Halla zgadza się z wielkością stablicowaną co do rzędu wielkości. Możemy to wywnioskować na podstawie wielkości koncentracji nośników ładunku obliczonej na podstawie stałej Halla. Koncentracja nośników ładunku obliczona na podstawie wyników pomiarów jest około kilkakrotnie wyższa od wartości tablicowej.

- 5 -

---