1. Mechanika górotworu - nauka o ruchach ( przemieszczenie, odkształcenie) i siłach (naprężeniach) jakie w związku z działalnością bud. podziemnego lub górn. powstają w górotworze.

Def. Górotwór - część skorupy ziemskiej , które stanowi przedmiot zainteresowania ze strony bud i gorn

Zadania mech. Gór. : a) poznawcze (badanie własności gór., badanie zjawisk zachodzących w gór., formułowanie praw rządzących tymi zjawiskami) b) praktyczne (tworzenie podstaw dla racjonalnego projektowania i prowadzenia działalności bud. I górn. )

Górotwór jako ośrodek materialny w polu grawitacyjnym ziemskim ( tzn posiada określoną masę):

Masa właściwa średnia w otoczeniu pktu A : ρ_śr=ΔM/ ΔV

Masa wł. W punkcie a: ρ=lim _{( ΔV->0)} ΔM/ ΔV= dM/ DV

Masa wł. górotworu jednorodnego: ρ=M/ V [kg/m³]

R=6.370km, H=1km, H/R=0,16%_o

Średni ciężar właściwy w oto górotworu: γ_śr=ΔQ/ ΔV

Powiązanie: ρ_*g=γ

Wartości orientacyjne:

γ =2,5*10⁴ [N/m³] , ρ=2,5*10³ [kg/m³]

2. Pierwotny stan naprężenia w górotworze:

Mamy z nim do czynienia, gdy górotwór jest nienaruszony działalnością górnicza. Ciężar objętościowy skal nadległych wynosi: Q= γ*F*H, dla elementarnego sześcianu. W celu wyodrębnienia składników pierwotnego stanu naprężenia analizujemy elementarną cząstkę górotworu o kształcie sześcianu znajdującą się na głębokości h pod powierzchnią ziemi. Zakładamy, że powierzchnia ziemi jest plaska, a nad sześcianem jest slup ścian nadległych poddanych działaniu sil ciężkości. Na cząstkę wywierane jest więc Q.

Pierwotne ciśnienie pionowe:

p_z=Q/F= (γ*F*H)/F= γ*H. strop i spąg elementarnego sześcianu jest poddany działaniu ciśnienia .Ciśnienie pionowe w gór. nienaruszonym naz. Ciśnieniem pierwotnym. Rozciąganie oznaczamy znakiem +,a ściskanie znakiem -, stąd p_z=- γ *H.

Pierwotne ciśnienie poziome:

Pod wpływem ciśnienia sześcian dostaje odkształcenia podłużnego, czyli jego h zmniejsza się, a wydłużają się krawędzie poziome. Możliwe jest to podczas jednoosiowego ściskania. W górotworze jednak obok elementarnego sześcianu są podobne sześciany. Jeżeli przyjąć, że w kier. poziomym gór. jest jednorodny wówczas sąsiednie sześciany mają podobną tendencję do odkształcania. W rezultacie nie dochodzi do odkształcenia na boki. Piszemy więc: ε_x= ε_y=0 i ε_znie0. można więc przyjąć, że górotwór jest półprzestrzenią mającą możliwość przemieszczania się w górę - dół. Skoro nie dochodzi do odkszt. elementarnego sześcianu ozn. to , że oprócz p_z działają jeszcze ciśnienie poziome p_x i p_y. Dla górotworu odpowiadającego prawu Hooke'a mamy związek naprężeń i odkształceń.: ε_x=1/E*( ε_x -ν*( p_y + p_z))=0, mamy więc ν*( p_y + p_z)=0, gdzie p_y = p_x.

Zakładamy izotropię w płaszczyźnie poziomej (p_y = p_x). Z układu równań widać, że ciśnienie poziome działające na boczne ścianki elementarnego sześcianu wynosi: p_y = p_x= ν/(1- ν)* p_z= p_z /(m-1). Składowe pierwotnego, trzyosiowego stanu naprężeń to : p_z=- γ*H, p_y= p_x= p_z /(m-1).

Wprowadzamy pojęcie współczynnika rozporu bocznego: λ=1/(m-1), mamy λ= p_x / p_z,, przy braku izotropii: λ_x* p_z= p_x, λ_y* p_z= p_y, zapis ten pozwala ocenić stan naprężenia, gdy gór. odpowiada nie tylko modelowi Hooke'a, ale i innym modelom. (Np dla gór. ziarnisto-sypkiego: λ=tg²(45°-φ/2), z tego mamy wniosek: że dla φ = 30°, pierw. ciśn.. poziome stanowi 30% ciśn. pionowego.)Mamy: mała głębokość (λ=0,1, m=12), duża głębokość(λ=1, m=2), czyli przy dużej głębokości p_y= p_x= p_z=p (stan geostatyczny- czyli we wszystkich kierunkach jednakowe ciśnienia). Im bliżej powierzchni tym bardziej zbliżamy się do stanu jednoosiowego ściskania. Możemy opisać ten stan tensorem naprężeń T_n=| |

W wielu rejonach kuli ziemskiej naprężenia w skałach są sumą tensorową napręż geostatycznych i tektonicznych- powstaje wówczas trójosiowy stan naprężeń, w którym wartości naprężeń głównych są różne i różna jest orientacja ich osi. Występowanie naprężeń poziomych większych niż pionowe jest charakterystyczna dla rejonów aktywnych tektonicznie ( mogą być większe 1,5 - 6 razy).

Wartość współczynnika rozporu λ w zależności od H zmienia się w granicach λ=100/H+0,3 do λ =1500/H +0,5.

3.Pierwotny stan odkształcenia górotworu

P.S.N.G. jest stanem przestrzennym, natomiast P.S.O.G. jest jednoosiowy ( ściskanie jest tylko na osi z), mamy ε_x= ε_y=0, tensor T_o=| |. Wartość pierwotnych naprężeń pionowych można określić z uogólnionego prawa Hooke'a: ε_z=1/E*( ε_z -ν*( p_x + p_y)),gdzie , p_y= p_x= νp_z /(1-ν), mamy więc: ε_z=1/E*(1-ν- 2ν²)/(1-ν)*p_z. a p_z=- γ*H, więc ε_z= -γ/E*(1-ν- 2ν²)/(1-ν)*H, czyli odkształcenie jest funkcją głębokości ε_z=f(H), a ν=ψ(H).Zależność odkszt pionowych od H jest zależnością krzywoliniową.

4. Stan naprężenia górotworu w otoczeniu wyrobisk korytarzowych (tuneli):

Wykonanie wyrobiska zmienia P.S.N. i O. na odkrytych ścianach wyrobiska siły powierzchniowe wynoszą 0, co jest powodem odkształcania się górotworu w kier dowolnej przestrzeni. Odkszt te jednak mogą być ograniczone reakcją założonej w wyr obudowy. Uwzględniając głębokość można sadzić o znacznej koncentracji napr pion jakie mogą wytąpić na ścianach bocznych tunelu. Napr pionowe w stropie i spągu wyr, w skutek odkszt gor. będą miały wartość mniejszą od składowej pion ciś pierw. Składowe poz naprężeń panujących w gór w sąsiedztwie wyrobiska porównywane są ze składowymi poz cis pierw. Wykazują tendencje odwrotne w ścianach bocznych (ociosach) chartka jest spadek napr poz. W stropie i spągu natomiast wyst ich koncentracja, gdy w gór nienaruszonym poprzez wykonanie wyrobiska lokalnie naruszymy stan napr, założenia te nie rozprzestrzenią się w nieskończoność. Powyższe zgodnie z zasadą Saint-Venonta będą zanikały wraz ze wzrostem odległości od miejsca zaburzenia. Naogól w mech gór przyjmuje się odl pięciokrotnie dluższą niż wymiary wyrobiska.

5. Tunel:

Jest to wyrobisko o stacjonarnych ścianach (ociosach), którego długość L znacznie przekracza wymiary przekroju poprzecznego.

Redystrybucja naprężeń:

Wn. Można stwierdzić, że: a) w stropie nast. Spadek napr Pio, a na samej linii stropu nawet do 0 b) w ociosach wyst wzrost napr pion, czyli koncentracja oraz spadek napr poziomych na samych ociosach do 0 c) w dostatecznie dużej odl od wyrobiska panuje stan pierwotny.

W zasadzie gór powinien być rozpatrywany jako układ przestrzenny, w uproszczeniu jednak wyst jako układ płaski, w przekroju prostopadłym do osi podłużnej wyrobiska przyjmując że wyrobisko ma bardzo dużą odl w porównaniu do przekroju poprzecznego. Z gór wycinamy więc tarczę dost dużą w stosunku do przekroju wyrobiska, w środku tarczy usytuowany jest otwór odpowiadający przekrojowi poprzecznemu wyrobiska. Tarcza obciążona jest na krawędziach składowymi ciś pierw gór (p_x i p_z). Rozpatrujemy więc płaski stan napręż:

I przypadek: wyrobisko przekrój kołowy:

Przyjmując, ze gór odpowiada modelowi Hooke'a, czyli jest to sprężysta tarcza z otworem kołowym. Dla takiego układu wykorzystamy 6.wzory KIRSHA:

Napręż radialne:

σ_r =1/2* p_z{1-(a/r)²-[1+3(a/r)⁴-4(a/r)²]cos2φ}+ 1/2* p_x{1-(a/r)²+[1+3(a/r)⁴-4(a/r)²]cos2φ}

Napręż obwodowe:

σ_t =1/2* p_z{1+(a/r)²+[1+3(a/r)⁴]cos2φ}

+ 1/2*p_x{1+(a/r)²-[1+3(a/r)⁴]cos2φ}

Napręż styczne:

τ =1/2*( p_z-p_x){1+2(a/r)²-3(a/r)⁴}*sin2φ}

Każda ze składowych naprężenia jest funkcją

p_x i p_z , które zależą od głębokości, względna odległość liniowa jest w stosunku:

σ=f(p_z(H),p_x(H),a/r, φ)

Spośród wszystkich punktów na tarczy najbardziej istotne są punkty na konturze wyrobiska, dla r=a rozpatrujemy dwa przypadki:

1) p_x =0 i p_z nie 0 - mała głębokość

2) p_x nie 0 i p_z nie 0 - duża głębokość

Dla r=a, gdzie a/r=1 mamy:

σ_r =0

σ_t =p_z{1+2cos2φ}+ p_x{1-2cos2φ}

τ =0

Napr radialne na konturze , czyli normalne do konturu wyrobiska są równe zero.

Podobnie napr styczne. Jedynie napr obwodowe są funkcją głębokości oraz kąta φ rozpatrywanego górotworu.

W stropie spągu wyrobiska (φ=90 lub φ=270)

Np: a) |p_z|>3|p_x| tzn m>4 lub λ<1/3 :

p_x=1/(m-1)p_z= λ p_z,charakt dla małych głeb, napr rozciagaja

b) |p_z|=3|p_x| tzn m=4 lub λ=1/8 : σ_t=0

c) a) |p_z|<3|p_x| tzn m=4 lub λ>1/8 , tu napr obwodowe ma ten sam znak co cis, czyli napr ściskające.

Wn przekrój kołowy dla małych głębokości nie jest korzystny, bo wyst napr rozc, korzystny jest natomiast dla gł dużych.

W ociosach wyrobiska (φ=0 lub φ=180)

σ_t=3p_z-p_x,gdy px=0 to σ_t=3p_z,gdy p_z=p_x to σ_t=2p_z

Napr obwodowe zawsze występują jako napr ściskające, gdy powyższe. W ociosach wyst napr pionowe o koncentracji: σ_t=3pz do 2pz,

Dla 1/3p_z>p_x r=a,σ_t=-p_z+3p_x,gdy 1/3p_z=p_x to σ_t=0

Gdy p_x=0 to σ_t=-p_z

Dla przypadku, gdy stan napr wokół wyrobiska jest geostatyczny, czyli gdy: p_z= p_x = p_y=p otrzymuje się rozw w postaci:

σ_t =p[1+(a/r)²]

σ_r =p[1-(a/r)²]

τ =0

Rozpatrujemy przykład, gdy wyrobisko narazone jest na działanie ciśnień wewnętrznych p'.

Wzory na naprężenia obwodowe i radialne przyjmują postać:

σ_t =p+(p-p')(a/r)²

σ_r =p-(p-p')(a/r)²

Przemieszczenie radialne dla dowolnego pktu okresla zależność:

u_r=3a²/(2E-r)*(p-p'),

gdy r=a mamy: u_r=3a/2E*(p-p'),

7.Wyrobisko chodnikowe

Przekrój prostokątny - rozkład napr wokół wyr

Na brzegach tarczy pierwotny stan napr odpowiada modelowi Hooke'a. zgodnie z rozw podanym przez Savina . W sąsiedztwie wyrobiska o wys w i szerokości R.

Ekstremalne wartości naprężeń pojawiają się na konturze.

W ociosach: σ_x = 0, σ_z = (1+α)p_z-p_x

w stropie i spągu: σ_x = (1+β)p_z-p_x , σ_z = 0,

Współczynniki kształtu zależą od wysokości i szerokości wyrobiska

L/w
α
β

Wielkości napr ni zależą od pola przekroju wyr lecz od stosunku szer do wys wyr

Nie projektuje się tuneli o stosunku L/w 50:1. przekrój ten jest bardzo niekorzystny. Wystepuje tam bowiem naprężenie rozc. Najlepiej wykonać tunele o stosunku 1:50, wtedy występuje tylko napr ścisk.

Z analizy wzorów na σ_x , σ_z wynika, że w ociosie p_z jest znacznie większe od p_x, dlatego σ_z w ociosie to napr ścisk .

W stropie mogą wyst 3 przyp:

a) gdy wyst σ_x wówczas mamy do czynienia z napr rozc

b) σ_x =0

c) σ_x - ściskane

Zależy to od stosunku p_z/p_x oraz od współczynnika β .

Na małej głębokości i dla L/W=50/1

Koncentracja naprężeń w ociosach jest

18-krotnie większa niż p_z, natomiast w stropie napr poziome σ_x=-p_z, czyli jest napr rozc. Na większej głęb, gdy p_x=p_z napr rozc znikają.

Wn. W ociosach wyrobiska prostokątnego zawsze wyst koncentracja pionowych napr scisk

Natomiast w stropie wyst napr rozc.

Wn. a) tunel o przekroju prostokątnym nie jest rozw dobrym. Prostokąt ma ostre naroża - w praktyce próbujemy je zaokrąglić

b) nie jest korzystne wykonywanie wyr o duzym stos L/w. należy więc projektować wyr tak,aby napr poziome (σ_x-rozc) były jak najmniejsze.

8. Stan naprężeń wokół wyrobiska o kształcie i przekroju eliptycznym.

Zgodnie z rozw Hubera ekstremum wartości napr występujących w wierzchołkach elipsy:

Dla I-I σ_x=-p_z+(1+2a/b)*p_x, σ_z=0

Dla II-II σ_z=-p_x+(1+2a/b)*p_z, σ_x=0

Rozkład napr w sąsiedztwie wyrobiska elipt jest nast.:

W zależności od stos a/b wyróżniamy różne kształty wyrobiska o przekroju eliptycznym.

a) a/b małe to napr w stropie są rozc, a w ociosach wyst duża koncentracja napr pionowych ściskających

b) a/b wzrasta to w stropie napr rozc stopniowo maleją,a w ociosach maleją napr ściskające

c) a/b tże σ_x=0 to znikają napr rozc w stropie, w ociosach napr ściskające nadal maleją. W takim wypadku mamy:

σ_x=-p_z+(1+2a/b)*p_x=0 i mamy: a/b= 1/2(p_z/p_x-1)

p_x/p_z=1/(m-1)=λ to a/b=(m-2)/2,

w stropie dla a/b=(m-2)2 to σ_x=0

d) a/b dalej wzrasta to elipsa wydłuza się w kierunku pionowym. W stropie zaczynają wzrastać napr ściskające poziome. Natomiast w ociosach nadal maleją napr ściskające

e) a/b tże σ_z (napr ścisk) w stropie i ociosach takie same to σ_x=σ_z:

-p_z+(1+2a/b)*p_x σ_x=-p_x+(1+2a/b)*p_z,

i otrzymujemy: a/b=p_z/p_x=m-1=1/ λ

Podsumowanie:

Przekrój eliptyczny jest korzystny dla wyrobisk korytarzowych, pod warunkiem dobrania odpowiednich stosunkow a/b. najkorzystniejsze przypadki to takie, gdy napr rozc znikają ,a w ociosach wyst jednakowe napr ściskające.

Gdy a/b= p_z/p_x to σ_x= σ_z =p_x+p_z,

Czyli najkorzystniejszym przypadkiem jest przypad , gdy napr SA sumą naprężeń pierwotnych.

Wnioski all tuneli

Korzystne jest wykonanie tunelu o przekroju eliptycznym, bądź zbliżonym do eliptycznego, gdy a/b=(m-2)/2, najkorzystniejszym przypadkiem jest, gdy a/b=m-1

Korzystne kształty wyrobiska eliptycznego można także przeanalizować w zależności od głębokości.

a)mała głębokość m=12

a/b=(m-2)/2=5, a/b=m-1=11

b) średnia głębokość m=4

a/b=(m-2)/2=1, a/b=m-1=3

c)duża i bardzo duża głębokość m=2

a/b=(m-2)/2=0 (brak rozc), a/b=m-1=1(koło)

Wielkość naprężeń w wyrobisku septycznym nie jest zależna od przekroju wyrobiska lecz od stosunku półosi elipsy. Przekroje o dużej szerokości są niekorzystne. Korzystne SA natomiast przekroje, których wysokość jest większa od szerokości, wówczas znikają napr rozc tak niebezpieczne dla skał,a napr ścisk osiągają wielkości umiarkowane niezależnie odwysokosci przekroju.

Przykładem mogą być olbrzymie komory w kopalniach soli i wymiarach kilkudziesięciu metrów i więcej, które utrzymują się doskonale nawet bez dod wzmocnień w postaci obudowy.

9. Teoria sklepienia ciśnień

Zakładamy, że w gór wykonano wyrobisko o niekorzystnym składzie wydłużone w kier poziomym). Dopóki wyrobisko będzie nieobudowane napr pionowe w stropie σ_z=0,a napr poziome σ_x będą napr rozciągającymi . ponieważ skały są mało odporne na rozc, dlatego napr często przekraczają granicę wytrz. Dochodzi wówczas do spękań skał, co powoduje, że napr pionowe w stropie spadają do zera. A w dostatecznie dużej odległości σ_x =R_r. Wokół wyrobiska powstaje więc strefa odprężona. Część skał opadnie do wyrobiska, które przyjmuje optymalny kształt. Linia w stropie jest miejscem geometrycznym punktów, gdzie nie jest przekroczona granica wytrz na rozc. Strop pierwotnie płaski stanie się stropem w kształcie sklepienia, które nosi nazwę sklepienia ciśnień.

W wyrobisku więc o niekorzystnym kształcie dokonuje się samoczynnie proces zmiany kształtu, co prowadzi do wystąpienia w otoczeniu wyrobiska strefy spękań (strefy odprężonej).

Wysokość strefy spękań można określić z zależności dla wyrobiska eliptycznego. Naprężenia poziome w stropie są równe:

σ_x=R_r, σ_x=-p_z+(1+2a/b)*p_x=R_r, mamy więc:

a/b=1/2(p_z/p_x-1+R_r/p_x)

uwzględniając , że: p_x=1/(m-1)p_z=λp_z, m=1/ν

otrzymujemy:

a/b=1/2(1/λ(1+R_r/p_z)-1) lub

a/b=1/2((m-1)R_r/p_z+m-2)

gdy na przekroju wyrobiska opisze się elipsę o stosunku półosi a/b jak we wzorze powyżej, wówczas wycinek elipsy, zawarty między wierzchołkiem elipsy a stropem stanowi strefę, gdzie skała jest odprężona i może opadać do wyrobiska., po przekształceniu: (wyliczamy a z obu wzorów powyżej).

Wysokość sklepienia ciśnień f można obliczyć z zależności: f=a-w/2, w-wysokość wyrobiska.

Przyjmując, że b=1/2Ll, wówczas półoś można określić następującą zależnością: a=1/4(1/λ(1+R_r/p_z)-1)*Ll lub

a=1/b((m-1)R_r/p_z+m-2)*Ll, Ll- szerokość wyr.

Przyjmując, że p_z = -γ*H otrzymujemy ostateczne zależności:

a=1/4(1/λ(1-R_r/(γ*H))-1)*Ll lub

a=1/b((1-m)R_r/(γ*H) +m-2)*Ll

Wn. a) półoś a jest wprost proporcjonalna do szer wyrobiska. Im szersze wyr tym wyżej sięga strefa odprężona.

b) Im skały słabsze(mniejsze niż R_r) tym wyższa jest strefa odprężona

c) Gdy wyr będzie bardzo dlugo stało, to przyjmie ono kształt taki, dla którego:

a/b= p_z /p_x =m-1

Gdy w stropie zostanie przekrocz wytrz na rozc i Rc w ociosach wyrobisko przyjmie taki kształt , aby: σ_z=σ_x= p_z +p_x

Dla wyrównania napr ścisk a=b/λ, gdy b=1/2 Ll, to a=1/(2 λ)Ll. Jeżeli wyrobisko jest na małej gł to λ=0,1.

10. Stan naprężenia w sąsiedztwie wyrobiska szybowego:

Szyby podobnie jak tunele mają nieduży przekrój poprzeczny. Dominującym ich wymiarem jest dł, a ściślej i głębokość. Problemy związane z wyr pionowymi można rozpatrywać jako zadanie płaskie wycinając myślowo w półprzestrzeni, w której jest wydrążony szyb, elementarną warstwę poziomą z otworem szybowym. Gór z pion szybem, czy otworem wiertniczym stanowi problem przestrzenny. Obciążenie bowiem wzdłuż osi nie jest stale. Ciśn. boczne zmienia się z głębokością.

Napręż radialne:

σ_r =p_x{1-(a/r)² }=(γ*H)/(1-m)*{1-(a/r)² }

Napręż obwodowe:

σ_t =p_x{1+(a/r)² }=-(γ*H)/(m-1)*{1+(a/r)² }

Napręż pionowe:

σ_Z =ν*( σ_r+ σ_t),gdzie r-odl w przyj ukł wspól walcowych

Zał.: a)przyjmujemy, że na brzegu otworu nie działają żadne siły zewn od środka

a)brzegi tarczy obciążone są składowymi poz ciś pierw

b) ze wzgl na znaczny wymiar wyr w kier osi pionowej, w stos do wymiarów poprzecznych mamy do czynienia z płaskim stanem odkszt.(czyli ε_z=0). Natomiast stan napr sprowadza się do stanu kołowo-symetrycznego.

War. Brzegowe:

a)w odl niesk. dużej od szybu: r->niesk. :

σ_r = σ_t =p_x -p_y

b)na konturze szybu (r=a) istn możliwość odkształceń σ_r =0

c) dla r=a σ_r =0, σ_t =2p_x, σ_z =2νp_x,

Bezwględna wartość naprężeń rośnie wraz z głęb

Rozpatrywanego przekroju do pewnej wartości granicznej uwarunkowanej krytycznym wytężeniem gór.

Dla wyzn głeb kryt, to jest takiej w którym nie objawia się cieśn. w obudowie, wykorzystujemy kryterium wytrzymałościowe de Saint Venant:

E*ε_kr=σ_r-ν(σ_t + σ_z)= -νR_c

Podstawiając uzyskamy wartości dla ścianki szybu: p_x=R_c/(2*(1+ ν))

Z zapisu uniwersalnego wynika, że:

p_x=p_y=λp_z=Hγ/(m-1)

Otrzymuje się gleb, poniżej której w skutek koncentracji naprężeń na ściankach szybu nastąpi przekroczenie granicy wytrz skal na ścisk.:

H_kr=Rc/γ*(1- ν)(2 ν(1+ ν))

Powyższa zależność dotyczy szybu wykonanego w skalach zwięzłych.

Głównymi czynnikami decydującymi o powstaniu nacisku na obudowę szybu jest głębokość oraz własności skal, przez które szyb przechodzi. W skałach mocnych nacisk ten na mniejszych głębokościach =0.

Począwszy od tej głębokości, aż do dna szybu skały znajdujące się w jego sąsiedztwie są w stanie spękania.

Wokół wytwarza się więc odmienny stan naprężenia. Określenie tego stanu polega na rozpatrzeniu równowagi układu sprężystego ze strefą spękań.

Gdy szyb na całej głeb przechodzi przez ośrodek sypki, to ciśnienie na obudowę szybu na głęb H równe jest cieśn. poziomemu w górotworze:

p_o=Hγ/c, gdzie c=(1+sinφ)/(1-sinφ), φ-kąt tarcia wewnętrznego

Ciśnienie na obudowę zależne jest zatem od cieśn. pion oraz od φ materiału. Przy skałach niejednorodnych bierze się pod uwagę sumę iloczynów γH. γ₁H₁+…+γ_nH_n=Σ γ_iH_i

11. Wyrobisko tunelowe w górotworze niejednorodnym:

Zakładamy, ze górotwór skalda się z 2 warstw o modułach sprężystości E₁ i E₂. tunel wykonano w warstwie 2, ma on przekrój kołowy o promieniu a. Grubość 2 warstwy ponad wyrobiskiem wynosi h. Na układ działa wszechstronne równomiernie ciśnienie p.

1° E₁<E₂

w tym przypadku warstwa górna przenosi prawie w pełni cieśn. wzdłuż linii granicznej na warstwę drugą niezależnie od grubości półki. Warstwę 2-gą można uważać za półpłaszczyznę z otworem kołowym. Wielkość napr zależna jest , w analizowanym rozw, od obciążenia P oraz współczynnika n.

n=(a+h)/a - sqrt[(a+h/a)²-1]

Napr poz w pkcie A wynosi:

σ_x=p/(1-n²)²[(1-n²)²+16n²]

napr obwodowe na brzegu otworu w pktach B i C: σ_t=2p

natomiast dla pktów D i E, dla których kąt 0<φ<90 napr osiągają wartości ekstra:

σ_t=2p[(1+n²)^/(1-n²)]²

2° E₁>E₂

Odmienny obraz otrzymamy w powyższym przypadku.

Przy cienkiej półce skały mają zdolność odkształcania się do wyrobiska, warstwa górna mająca duży moduł sprężystości już przy małych odkształceniach odpręży się w całości i wskutek tego ciśn. wywierane przez nią na półkę będzie minimalne. Wielkość napr w półce będzie mała, mniejsza niż w ukł jednorodnym.

12. Obciążenia czynne obudowy tunelu:

Podst zad stawianym przez mech gor jest utrzym stateczności, przez którą rozumiemy zapewnienie wymaganych gabarytów wyrobisk w całym okresie ich użytkowania.

Spełnienie tego war możliwe jest poprzez właściwy dobór obudowy. Można tego dokonać poprzez przyjęcie modelu zjawiska zachodzącego w gór w wyniku wykonania wyrobiska. W każdym przypadku należy określić wielkość obciążenia na obudowę, które często nazywa się ciśnieniem gór.

W pierwszych pracach dotyczących obciążenia czynnego przyjmowano, że w stropie wyrobiska powstaje naturalne sklepienie w granicach, którego skały są zniszczone, a ich ciężar określa się nast.:

Q= γ*F*1mb, F=2/3*Ll*h(pole wycinka elipsy)

Mamy: Q=2/3* γ*Ll*h

13. Metoda Protodiakonowa

Kształt sklepienia określa się z warunków równowagi linii sklepienia, z sumy momentów wzgl pktu C

M=T*y-qx²/2, y= qx²/2T,

q-ciśn pochodzące od ciężaru nakładu, T- siła osiowa w strzałce sklepienia, (x,y)-współrzędne

Sklepienie nat ma kształt paraboli 2-go stopnia. Oddziaływanie tego sklepienia można rozłożyć na składową pionową P i poziomą T. Składowa poz powoduje przemieszczanie się pktu A, czemu przeciwdziała tarcie μ*P , μ=tgφ, P=q*a.

Z rzutu sił na kier poziomy wynika, że równ w pktcie A sklepienia: ,T+r*h=μ*q*a, T= qa²/2h

- τ obciążenie równomiernie rozłożone, skierowanie w stronę sklepienia

- τ*h siła charakteryzująca opór przesuwu

Po podstawieniu:

qa²/2h+ τ *h =μ*q*a, wyliczamy τ, przyrównujemy równ wzgl h do zera:

a-μ*h=0,h= a/μ

Wys sklepienia naturalnego= iloraz połowy szer wyr przez współczynnik tarcia.

13. Metoda znajdowania zastosowania do ośrodków rozdrobnionych.

Protodiakonow uogólnił również teorię do skał zwięzłych wprowadzając w miejsce współ tarcia wskaźnik zwięzłości, który w przybliżeniu wynosi:

f_P=0,1R_c, R_c -wytrz doraźna na ścisk

Obciążenie pochodzące od ciężaru skal nadległych, a oddziaływujące na 1m wyrobiska:

Q=2/3*2*a*h*γ=4/3*γ*a²/μ,

Czyli obc przypadające na jedne odrzwia obudowy, gdy krok (rozstaw) obudowy =L1 wynosi: Q=4/3*γ*a²/μ*L1

Wn. Obciążenie obud wzrasta z kwadratem szer wyrobiska

14.Metoda Sałustowicza:

Na konturze wyrobiska prostokątnego opisana jest elipsa o stosunku półosi n=a/b.

Przyjmuje się, że przekrój strefy odprężonej jest odcinkiem paraboli. Ciężar strefy odprężonej przypadającej na 1mb długości wyr. wynosi:

Q=2/3*2*L1*h*γ, h=a-w/2, Q-ciężar obj skał

Do wyznaczenia wartości a i b wykorzystuje się równanie na stosunek osi elipsy:

a/b=1/2*[m-2+(m-1)*R_r/p_z], z²/a²+x²/b²=1, mamy więc: a=sqrt[(w/2)²+n²(L1/2)²], a/b=n

Znajomość wart a powoduje określenie wysokości strefy odprężonej, a nast. Obc na obudowie Q na 1mb.

Z analizy wzorów wynika, że obud uzależniona jest od głęb, na której znajduje się wyrobisko. Również wytrz skały stropowej na rozc uzal jest też od współ Poissona skał, ciężaru objęt skały i wymiarów wyrobiska.

15. Metoda Cymbariewicza:

Według Cymbariewicza prócz strefy odprężonej w stropie powstaje strefa spękań wśród ociosów. Kształt powstałego sklepienia to wycinek paraboli DEF którego wysokość z rysunku wynika CF=h=CE/tgφ. Obciążenie pionowe pochodzi od skał zwartych w strefie górotworu A'B'GH a obciążenie poziome jest wynikiem tarci po płaszczyznach poślizgu AD, BE. Podstawa strefy odprężonej w stropie wynosi

L=2a+2w*tg(45-(φ/2))

Obciążenie dla sklepienia w kształcie wycinka paraboli równe jest

Q=2/3*L*h* γ

Dla sklepienia w kształcie trójkąta ( np. w górotworze uwarstwionym obciążenie na obudowę przypadające na jednostkę długości wyrobiska wynosi

Q=l/2*h*γ , h=a/2f

Rozkład ciśnienia bocznego zależy od wymiarów wyrobiska przyczym przy stopie: p_xmin=γ*h'*tg² (45-(φ/2)) przy spągu

p_xmax= γ*(h'+w)*tg² (45-(φ/2)) = γ*λ*(h'+w) W metodzie nie uwzględnia się głębokości posadowienia wyrobiska chociaż uwzględnia się zniszczenie skał w skutek przekroczenia ich wytrzymałości na całym konturze wyrobiska

Metoda Bierbaumera

według niego ciśnienie stropowe działające na obudowę równe jest ciężarowi słupa skały o podstawie = szerokości wyrobiska i wysokości = odległości wyrobiska od powierzchni ziemi Wtedy P=γ*H*l Na płaszczyznach AB i CD działają siły tarcia przeciwdziałające przesuwaniu się skał. Siły te są wynikiem działania ciśnienia poziomego w górotworze T=μZp_zśrH μ=tgφ , μ =1/(m-1),

P_zśr =1/2* γH T=1/2 μλ γH²

Według Bier. obciążenie budowy jest równe ciśnieniu stropowemu pomniejszonemu o wielkość sił tarcia Q=P-2T, Q= γHl- μ λ γH² Metoda uwzględnia wpływ głębokości na wielkość ciśnienia na obudowę Q=f(H)

dla H=0 Q=0, H=1/ (μ λ) Q=0,

H=l/(2μ λ) Q= γLl² /(4μλ).

Teoria jest słuszna w następującym zakresie głębokości 0<=H/(2μ λ) przyczy max obciążenie

Q_max= γLl² /(4*μλ).

Wzór jest słuszny gdy H nie jest dużo większe od l (do 20-25m). Na większej głębokości wystąpi skupienie ciśnień wówczas

Q= γ*l /(2 tg φ)

Metoda Kłeczka

Metoda łączy teorie Cymbariewicza i Sałustowicza. Oś pozioma elipsy sklepienia ciśnień została powiększona w stosunku do szerokości wyrobiska których wielkość zależy od wysokości wyrobiska b=l+2(w/2)*ctg(45+(φ/2))

a/b=1/2(m-2 +(m-1)*(R_r/P_z))

a=(L+wctg(45+(φ/2)))*(R_r+p_z+p_x)/2p_x

Wykorzystujemy równanie elipsy : (z²/a²)+(x²/b²)=1

dla x=l/2 z= (a/2)*sqrt(1-(L1/b)²

Obciążenie stropu wyrobiska ze stropu sklepienia

Q= γ(Ll(z-(h/2)+2/3*Ll((a/z)-2),

Q= γLl((z+a)/3-(w/2),

Q₀= (λγ)/2*[((πab-(b-1)w)/4)-2/3*Ll(z=a)]

Metoda opisuje obciążenie statyczne na obudowę wyrobisk korytarzowych a uwzględnia podstawowe parametry wytrzymałościowe skał.

Metoda Therzaghiego

W teorii T. badana jest równowaga elementu gor znajdująca się w sklepieniu wyrobiska prostokątnego posiadająca d_z (wymiar pionowy). Element rozpatrywany znajduje się w stanie równowagi pod działaniem następujących obciążeń:

-obciążenie pionowe nadkładu σ_zLl ,

-reakcja podłoża (σ_z+dσ_z)Ll,

-ciężar własny Ll* γd_z ,

-siły spójności wew. fd_z,

-poziome siły tarcia bocznego σ_xd_z.

Jeżeli parcie boczne będzie wyrażone za pomocą sił tarcia T=σ_xd_ztgφ to równanie równowagi rzutów sił w kierunku pionowym: σ_xLl-(σ_z+dσ_x)*Ll+ Ll* γd_z-2fd_z-2 σ_xd_ztg φ=0. Przy uwzględnieniu zależności między naprężeniami pionowymi a poziomymi oraz po przekształceniach równań można zapisać w postaci:

(dσ_z)/[ ((Ll* γ)/2)-f-λ σ_ztg φ]= 2d_z/Ll

a po scałkowaniu wyżej wymienionego wzoru i obciążenia nadkładu otrzymamy

σ_z=[((Ll* γ)/2)-f]/ (λ tg φ)*[1-e*z(2λtgφ)/Ll]+p₀e*z(2λtgφ)/Ll

Obciążenie pochodzące ze stropu a przypdające na jeden metr długości wyrobiska określa zależność:

Q=Ll[((Ll* γ)/2)-f]/ (λ tg φ)]*[ 1-e*z(2λtgφ)/Ll]+ p₀e*z(2λtgφ)/Ll

Wielkość p₀ oznaczać może także ciśnienie spowodowane naporem wód podziemnych. Jeżeli to ciśnienie nie występuje wtedy:

Q=Ll[((Ll* γ)/2)-f]/ (λ tg φ)]*[ 1-e*z(2λtgφ)/Ll]

Przyjmując za Therzaghim że dla dużych głębokości skał λ=1, p₀=0 wówczas wykazuje duże podobieństwo do zależności podanej przez Protodiakonowa Ll/ tg φ (strzałka sklepienia ciśnień)

Metoda Beniowskiego według niego wielkość sklepinia ciśnień nad wyrobiskiem może być określona za pomocą wzoru uwzlędniająącego wskaźnik jakości górotworu

h=(100-RMR)*Ll/100

RMR- wskaźnik jakości górotworu opisuje jakość górotworu poprzez sumę not punktowych przypisanych następujący parametrom:

-wytrzymałości na jednoosiowe ściskanie R_c

-wskaźnik stopnia spękania masywu skalnego RQD

-średnia odległość między płaszczyznami siatki spękań

-stan płaszczyzny nieciągłości

-stopień zawodnienia masywu skalnego

-położenie płaszczyzn nieciągłości

Dla zastosowań w górnictwie uwzględnia się podobnie jak w teorii Protodiakonowa lub Saustowicza

Klasyfikacje geotechniczne masywu skalnego

Jakość górotworu może być określona za pomocą punktacji klasy frakcji geotechnicznych opartych na podstawowych danych geologicznych, geomechanicznych, hydrogeologicznych, górniczych. Na podstawie sumarycznej punktacji ocenionych cech wyznacza się klasy jakości górotworu parametry stosowane w obliczeniach stateczności wyrobisk i dobiera się rodzaj budowy do konkretnych warunków. Klasyfikacji używa się głównie do oceny przydatności masywu skalnego przy projektowaniu budowli podziemnych i powierzchniowych. Podstawowym celem klasyfikacji jest dostarczenie informacji czy układ górotworu i budowla podziemna jest długotrwale stateczny. Do najbardziej znanych klasyfikacji geotechnicznych masywu skalnego należą RMR i Q. Z obu klasyfikacji uzyskuje się wartości ocen punktowych które można związać z podstawowymi parametrami ośrodka skalnego co jest korzystne w modelowaniu. Punktacja podstawowa w systemie RMR opiera się na 6 parametrach. W oparciu o punktacje RMR opracowuje się empiryczne własności podstawowych parametrów mechanicznych wykorzystywanych w modelowaniu numerycznym i analitycznym

E_m[GPa] =2RMR 100 dla RMR>=58

E_m[GPa] =(10RMR*10)/40 dla RMR<58

RQD wskaźnik ten opisuje procentową zawartość RQD=(Llp*100%)/Ll odcinków rdzenia większą od 2 razy jego średnicy w stosunku do całkowitej długości rdzenia.

RMR_k zmodyfikowany wskaźnik dla potrzeb kotwienia górotworu

Q=(RQD)/I_n*I_r/I_a*I_w/SRF E_m=25logQ

I_n wskaźnik systemów spękań

I_r wskaźnik chropowatości powierzchni spękań

I_a wsk. przeobrażenia płaszczyzny nieciągłości

SRF wsk. stanu naprężenia

Uśrednione właściwości górotworu, jakie uzyskuje się za pomocą klasyfikacji biotechnicznej wynikają z empirycznych ocen wielu cech górotworu. Posługiwania się tymi klasyfikacjami wymaga doświadczenia i znajomości procesów zachodzących w górotworze. Klasyfikacje geotechniczne akceptowane są przez projektantów pozwalają bowiem na częste zmiany konstrukcji obudowy w zależności od zmian własności górotworu.

Ciśnienie deformacyjne górotworu

Ciśnienie statyczne- było dotychczas w ociosach obudowy

Ciśnienie deformacyjne- ;pojawia się zaraz po wydrążeniu wyrobiska zanim założymy obudowę powoduje przemieszczenie warstw skalnych szybki proces (uwzględniamy czas)

Przyczyną ciśnienia deformacyjnego jest przemieszczenie się cząstek górotworu będących na konturze wyrobiska ku środkowi przekroju przy jednoczesnym przeciwstawianiu się tym przemieszczeniom przez założoną w tym wyrobisku obudowę. Ciśnienie deformacyjne występuje w ośrodkach sprężystych lub sprężysto-plastycznych. Dla oceny tego ciśnienia należy uwzględnić stan naprężeń i przemieszczeń górotworu o własnościach reologicznych. Wielkość jego w dużym stopniu zależy od głębokości:

Mała głębokość wielkość ciśn.def. jest niewielka, deformacje są małe przy czym występują one prawie natychmiast po wykończeniu wyrobiska przed ustawieniem obudowy. Sprężystość ośrodka lub czysto plastyczne odkształcenia są natychmiastowe i ustają zanim założą obudowę

Średnia głębokość przemieszczenia rosną stopniowo w czasie, obudowa w tym przypadku poddawana jest działaniu ciśnienie statycznego i def. przy czym osiąga ono wartości umiarkowane.

Duża głębokość odkształcenia rosną w sposób nieograniczony zachowanie się górotworu odpowiada ośrodkowi sprężysto-plastyczno-lepkiego w którym przemieszczenia osiągają duże wartości. Również ciśnienie w takich ośrodkach na budowie osiąga duże wartości. C. def. jest więc funkcją czasu a jego wielkość wzrasta od 0 do pewnej wartości x_t stopnia wraz z czasem .Zmiany w czasie są więc zależne od własności górotworu i charakterystyki obudowy

Δa=u=(p-p₀)*3a/2E

Dla wyrobiska o przekroju kołowym dowolnego punktu obwodu określa powyższa zależność

Przyjmując p=pz=px i ν=0,5 przyjmujemy że ośrodek jest nieściśliwy. Dla niego E=3G więc

u=(p-p₀)*a/2G

Stad mamy zależność na ciśnienie górotworu na obudowę p₀=p-u*(2G/a)

Sztywność obudowy μ=(E'd)/a²

Przyjmijmy że sztywność obudowy o kształcie pierścienia charakteryzuje współrzędna powyżej możemy napisać że

p₀=p/(1+2G/aμ)

obudowa ma charakter sprężysty tzn. oddziaływanie na górotwór proporcjonalne do przemieszczeń

Ciśnienie def. górotworu na obudowę zależy od:

-naprężeń pierwotnych (p), czyli od głębokości

-sztywności obudowy (μ) im obudowa sztywniejsza tym większe ciśnienie

-wartość odkształcenia górotworu jakie wystąpiło od wykonania wyrobiska do założenia obudowy

-modułu G (sprężystości postaciowej), przy dużym G odkształcenia są mniejsze tym samym i obciążenia

-od promienia wyrobiska

Powyższe dotyczą sytuacji gdy ośrodek pozostaje stale w stanie sprężystym tzn. w żadnym jego punkcie nie następuje przekroczenie granicy wytrzymałości

W badaniach własności skał i zjawisk zachodzących w górotworze wykorzystuje się zasady reologii czyli nauki o przebiegu procesów odkształcania się ciał po obciążeniu i zmianami naprężeń z uwzględnieniem czasu. Chcąc określić własności reologiczne oraz ocenić proces niszczenia ośrodka skalnego należy określić zależności σ i ε przy t=const.

Najważniejsze przejawy własności reologicznych ośrodka skalnego:

-zjawisko pełzania (zj. ciągłego wzrostu odkształceń z upływem czasu przy σ=const.)

-odc 1-2 obrazuje odkształcenia które występują natychmiast po przyłożeniu obciążenia

-2-3 wzrost odkszt. Wstąpił on przy σ=const (czyli właściwe pełzanie). W chwili t2 zdjęto obciążenie, napr. Spadły do zera, jednakże wtedy nastąpiło nagłe zmniejszenie odkszt co pokazuje 3-4

-następnie rozpoczyna się proces zmniejszania odkształceń asymptot aż do 0

Na krzywej pełzania można wyróżnić 3 stadia

1.Nieustannego pełzania skały

2.Ustalonego pełzania przy σ=const

3.Wzrostu szybkości odkształceń i zbliżającego się zniszczenia skały

Całkowite odkształcenia skały w dowolnym czasie są równe ε=ε_s+ε_p

Szybkość odkształceń: dε/dt = dε_s/dt + dε_p/dt

Równanie pełzania:

dε/dt = (1/E)dε_s/dt + σ/E*t₀

gdy σ=const

dε/dt = σ/E*t₀

-zjawisko relaksacji (spadek naprężeń z upływem czasu przy stałym obciążeniu)

-odcinek 5-6 przedstawia σ₀ (występuje nagle gdy przyłożone do próbki obciążenie wywołuje odkształcenia)

-6-7 przedstawia spadek naprężeń zachowanych przy stałej wartości ε=const. Czyli właściwa relaksacja

-w chwili t₄ usunięto odkształcenia przez przyłożone naprężęnia o kierunku działani przeciwnym do pierwotnego i wartości σ₀ (odc.7-8). Pomimo usunięcia odkształceń (powrót próbki do postaci pierwotnej) występują w niej pewne naprężenia o znaku przeciwnym do poprzedniego które nastąpiły w wyniku relaksacji

Czas w którym naprężenie zmniejsza się nazywany jest czasem relaksacji

Pełzanie i relaks są zjawiskami tego samego reologicznego odkształcania się skały gdy możliwe jest swobodne odkształcenie ujawnia się pełzanie gdy odkształcenie ograniczone to zachodzi relaksacja naprężeń . Zakładamy że ośrodek rzeczywisty ma cechy ciała sprężystego lepkiego i plastycznego przyjęto dla każdej z tych cech pewne symbole.

-właściwości sprężyste modeluje idealna sprężyna

-wł. lepkie perforowany tłok poruszający się w cylindrze wypełnionym cieczą

-wł. plastyczne suwak

Wykorzystując elementarne modele reologia poprzez ich łączenie buduje skomplikowane modele ciał rzeczywistych.

a)ciało sprężyste Hooke'a

b)ciecz lepka Newtona

c)ciało sprężysto-lepkie Kelwina

d)ciało sprężysto-lepkie Maxwella

e)ciało sprężysto-lepkie Poytinga-Thompsona

Tłok perforowany imituje właściwości lepkie materiału.

Posługując się wyróżnionymi elementarnymi modelami, reologia, przez ich łączenie buduje bardziej skomplikowane teoretyczne modele ciał rzeczywistych.

Zakłada się, że naprężenia we wszystkich połączonych elementach są jednakowe, natomiast odkształcenia całego modelu są sumą odkształceń poszczególnych el. Jeżeli el. Połączone są równolegle, to z kolei odkszt są takie same, a całkowite naprężenie jest sumą napr panujących w poszczególnych el.

Model Kelwina - odpowiadają piaskowce:

Do ciała Maxwella zbliżone są sól kam, łupki ilaste.

Wpływ czasu na kształtowanie się ciśnienia deformacyjnego:

- ośrodek Kelwina (zależność odkszt a napr)

σ=E*ε+η*dε/dt σ=E*ε+η*ε'

dε/dt -ozn, że nie nast od razu po obciążeniu

Zjawisko to nosi nazwę opóźnionej sprężystości.W przypadku wyrobiska kołowego zależność między napr i odkszt jest nast:

σ_r- σ=2G(ε_r- ε)+2η*( ε'_r- ε' ),

σ_t- σ=2G(ε_t- ε)+2η*( ε'_t- ε' )

Przemieszczenia poszczególnych pktów mają kierunek radialny i są funkcjami współrzędnej r i czasu t. Ze względu na przyjęty warunek nieściśliwości (ε= ε'=0, ε_r+ε_t=0), u=A(t)/r

Po scałkowaniu: du/dr+u/r=0

Na podstawie równości poprzednich, określamy odkształcenie i prędkość odkształcenia:

Mamy: ε_r=du/dr= - A(t)/r²,

ε_t= u/r=A(t)/r²

ε'_r=d²u/drdt= - dA(t)/dt*1/r²,

ε'_t= 1/r*du/dr= dA(t)/dt*1/r²

Po podstawieniu wartości odkształceń:

σ_r=σ - (2GA+2η*da/dt)*1/r²,

σ_t=σ + (2GA+2η*da/dt)*1/r²,

Powyższe zależności podstawiamy do równania równowagi: dσ_r/dr+( σ_r- σ_t)/r=0,

i mamy (wstawić σ_t i σ_r), gdy dσ/dr=0, σ=B(t),

gdy r-> niesk to σ_r=p => B(t)=p mamy:

σ_r= p- (2GA+2η*dA/dt)*1/r²

Z dotychczasowych rozważań wiadomo, że napr radialne na konturze otworu kołowego = oddziaływaniom obudowy:

σ_r=a= p- (2GA+2η*dA/dt)*1/a²,

σ_r=a=μ*u= μ*A/a, gdzie μ - sztywność obudowy

μ=E/*d/a², E'-moduł spr obudowy, d- średnica pierś obudowy, a- promień wyr

Przekształcając mamy:

dA/dt=p*a²- (2G + μ *a)*A/2η lub

dt/2η=dA/[p*a²- (2G + μ *a)*A] i całkujemy:

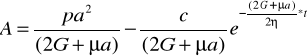
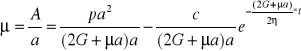
μ - przemieszczenie dowolnego pktu dolnego wyrobiska.

Dla t=0, u=0 mamy:

Ciśnienie pierw na obud=wart napr radialnych

σ_r=a=p₀=μ*u, mamy więc:

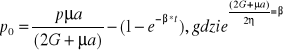
Gdy t=0, zatem ciśnienie na obudowach =0.

Wraz z upływem t, cieśn. wzrasta, zmierzając asumpt do wart końcowej:

W ośrodku Kelwina pierwotne ciśn gór na obud wyr wzrasta od 0 do wart końcowej, która jest < od napr pierw. Wartość ta zalezy od glęb i sztywno bud.

Jeśli więc zastosujemy obud podatną zezwalającą na odkszt się gor, to ciśn to poważnie się zmniejszy. Parametr β jest w tym przypadku mniejszy. Dod czynnikiem dział korzystnie jest ustawienie obud po upływie pewnego czasu od chwili wykonania wyrobiska.

Ośrodek Maxwella:

Zależn odkszt i napr:

σ_t- σ = 2η*( ε'_t- ε' )+ τ(σ'_t- σ'),

σ_r- σ = 2η*( ε'_r- ε' )+ τ(σ'_r- σ'),

τ - czas relaksacji naprężeń τ= η/G

Wstawiamy do równania równowagi:

dσ_r/dr+( σ_r- σ_t)/r=0, u=A/r

dσ_r/dr = 4^η/r³*dA/dt - τ*d²σ_r/drdt i całkujemy

Otrzymujemy:

σ_r=B(t)+R(r)*T(t), gdzie: ω=aμ/(2η+ητa), analogicznie do modelu Kelwina uzyskujemy:

Podsumowanie:

Końcowe cis na obud w ośrodku Maxwella, zawsze = wartości napr pierw gór. Zast obud podatnej nie prowadzi tu do zmniejszenia tego ciś. Powoduje ono jedynie powolniejszy przyrost tego ciśnienia.

Model Kelwina - odp skałom chartka się opóź sprężystym

Model Maxwella - od ośrodkom, w których wyst zjawisko relaksacji

W skałach na ogół obserwuje się oba te zjawiska równocześnie. War te spełnia model standard:

Ośrodek Poyntinga - Thomsona (standard):

σ = 2Gε + 2ηε' + τσ',

(σ_t- σ) + τ (σ'_t- σ') = 2G*(ε_t- ε) + 2η*(ε'_t- ε')

(σ_r- σ) + τ (σ'_r- σ') = 2G*(ε_r- ε) + 2η*(ε'_r- ε')

Odejmujemy stronami:

(σ_t- σ_r) + τ (σ'_t- σ_r') = 2G*(ε_t- ε_r) + 2η*(ε'_t- ε_r')

Przyjm war nieściśliwości, wyzn. Przemieszczenia jako funkcję czasu oraz wykorzystując równ równowagi wew otrzymujemy podst równ różn, które po scałkowaniu ma postać:

σ_r=B(t)+R(r)*T^(t),

Po wyzn war brzegowego dla r-> niesk, σ_r->p

mamy: B(t)=p, R=2δ/r², T^=pa²/2δ - Aaμ/2δ

gdzie δ=(GA+ η A)/(T+τT^), σ_r=μA/a

Uzyskane wart napr rad na obwodzie wyr:

Napr w dowolnym pkcie, w odl r od pocz ukł:

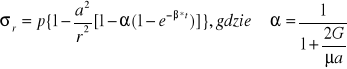
Gdzie wzory te dla t=0 przyjm taką samą wartość jak w ośr spręż , natomiast gdy t->niesk to napr zmierzają asympt do nast. wielkości:

r=a, dla t=0, σ_r=0, σ_t =2p

dla t=niesk, σ_r=αp, σ_t =2p- αp

Przemieszczenia radialne na brzegu otworu:

Wnioski:

a) Ciśnienie deformacyjne wywierane przez górotwór nie zależy wyłącznie od własności górotworu lecz od sposobu współdziałania górotworu z obudową

b)O ile w górotworze sztywny, można stosować obudowę sztywną o tyle w górotworze łatwo odkształcalnym należy stosować obudowę podatną

c) Ciśnienie def. można skutecznie zmniejszyć dobierając odpowiedni rodzaj obudowy w zależności od własności górotworu

d) Skutecznym środkiem obniżenia ciśnienia górotworu na obudowę jest opóźnienia w jej założeniu w wyrobisku. W górotworze idealnie sprężystym wystarczy nawet małe opóźnienie aby spowodować obniżenie c. def. nawet do zera

e) Ciśnienie deformacyjne można skutecznie zmniejszyć stosując przed założeniem ostatecznej obudowy sztywnej, tymczasową podatną. Czas pozostawienia tej obudowy powinien być dłuższy im sztywniejszą obudowę mamy zamiar ostatecznie zastosować.

---