LISTA ZADAŃ NR 6,7 Z MATEMATYKI DYSKRETNEJ
Algebra i teoria liczb
1. Zbadać czy funkcja f(x,y) jest działaniem w zbiorze A dla:
a) f(x,y)=x+y+1 i A=N,
b) f(x,y)=x-y-1 i A=Z,
c) f(x,y)=x⋅y+1 i A=N,
d) f(x,y)=x/y+x i A=Q,
określić własności działań, wyznaczyć element neutralny działania oraz element odwrotny do każdego a∈A i sprawdzić czy zachodzi dla działań prawo skracania.
2. Czy zbiór A z działaniem f(x,y) jest półgrupą oraz czy jest grupą:
a) A=Q f(x,y)=x+y-1,
b) A=N f(x,y)=x+y,
c) A=Q f(x,y)=x-y,
d) A=R f(x,y)=x⋅y,
e) A=Q\{0} f(x,y)=x⋅y.
3. Wyznaczyć tablicę działania ° dla grupy permutacji S3.
4. Obliczyć σ-1, τ-1,τ°σ, σ°τ oraz τ°σ2,σ°τ2 dla
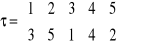
i 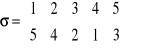
.
5. Zbadać czy poniższe algebry są pierścieniami
a) (Z,+, ⋅),
b) (W[x],+,⋅) , gdzie + to działanie dodawania wielomianów, ⋅ to działanie mnożenia wielomianów,
c) ({0,1,2}, +,⋅) gdzie działania określone są tablicami:
+ |
0 |
1 |
2 |
|
⋅ |
0 |
1 |
2 |
0 |
0 |
1 |
2 |
|
0 |
0 |
0 |
0 |
1 |
1 |
2 |
0 |
|
1 |
0 |
1 |
2 |
2 |
2 |
0 |
1 |
|
2 |
0 |
2 |
1 |
6. Zbadać czy relacja ℜ={(x,y)x∈R ∧ y∈R ∧ x=y } jest kongruencją a) w algebrze (R,+),
b) w algebrze (R,⋅).
7. Wyznaczyć NWD i NWW dla par liczb:
a) a=56 i b=35, b) a=309 i b=186,
c) a=233 i b=144, d) a=12378 i b=3054,
e) a=6409 i b=42823.
8. Wyznaczyć liczby całkowite x i y takie, że ax+by=NWD(a,b)
a) a=56 i b=35, b) a=309 i b=186,
c) a=233 i b=144, d) a=12378 i b=3054.
9. Rozwiązać równania
a) 3x=1 w Z5, b) 5x=3 w Z6,
c) 7x=5 w Z9, d) 2x=1 w Z4.
10. Wyznaczyć rzędy poszczególnych elementów w grupach multiplikatywnych:
a) Z*7, b) Z*12 c) Z*14,
czy są to grupy cykliczne?
Wyszukiwarka