SPR F 80, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka


Grupa laboratoryjna: 204 Nr ćwiczenia: 80

W skład grupy wchodzą:

Temat ćwiczenia:

Wyznaczanie długości fali świetlnej za pomocą spektrometru siatkowego

Wydział: Ochrona Środowiska

Semestr: Drugi

Studia: Dzienne-Inżynieskie

Dyfrakcja fali świetlnej polega na zmianie kierunku biegu fali wówczas, gdy trafia ona na przeszkodę lub przechodzi przez szczeliny. Dyfrakcja jest obserwowana wtedy, gdy wymiary otworów są porównywalne z długością fali świetlnej.

Siatka dyfrakcyjną jest przezroczysta płytka, na której nacięto szereg równoległych rys o jednakowej szerokości i ułożonych w jednakowych odstępach. Te odstępy spełniają rolę szczelin przez które może przechodzić światło. Jeżeli na siatkę pada światło to na każdej ze szczelin zostaje ono ugięte pod kątem . Jeśli postawi się na drodze ugiętych fal soczewkę oraz ekran w płaszczyźnie jej ogniska, to fale będą się skupiać w punktach 1, 2, ... ekranu. Tak więc każdemu punktowi ekranu odpowiada inny kąt ugięcia światła wychodzącego z siatki. Kąty ugięcia są takie, że fale spotykają się na ekranie w fazach zgodnych lub przeciwnych. Gdy spotykają się w fazach zgodnych dochodzi do wzmocnienia fali i spełniony jest warunek, że różnica dróg świetlnych jest całkowitą wielokrotnością długości fali, =k. Gdy dochodzi do wygaszenia fali spełniony jest warunek =(2k+1)/2. W pierwszym przypadku mamy jasny prążek, a w drugim mamy ciemny prążek na ekranie. Gdy za k będziemy podstawiać kolejne liczby naturalne otrzymamy wzory na prążki pierwszego, drugiego,... rzędu które można zaobserwować na ekranie. W przypadku światła białego jasne prążki poszerzą się i będą przyjmowały różne zabarwienie (od fioletu do czerwieni). Tak więc różnym zabarwieniom odpowiadają różne długości fali. Taki układ barw nazywamy widmem. Otrzymujemy układ widm pierwszego, drugiego i dalszych rzędów symetrycznie rozłożonych względem prążka centralnego.

Mierząc kąt dla prążków o różnej barwie można wyznaczyć odpowiadające im długości fali oraz dyspersję kątową siatki.

Aby obliczyć długość fali trzeba podstawić do wzoru =csin warunek na wzmocnienie fali =k, przez co otrzymuje się równanie csin=k.

Dyspersja kątowa siatki jest scharakteryzowana wzorem 0x01 graphic
, różniczkując równanie csin=k otrzymamy wzór 0x01 graphic
.

Do wyznaczania długości fali stosuje się spektrometr siatkowy, który składa się z kolimatora, siatki dyfrakcyjnej, stolika ze skalą kątową oraz lunetki. Kolimator składa się z szczeliny liniowej i kondensatora. Przymocowany jest do stolika ze skalą kątową, siatka dyfrakcyjna jest przymocowana do ruchomej części stolika. Padające promienie światła z kolimatora na siatkę zostają ugięte i wpadają do lunetki. Lunetka składa się z obiektywu i okularu. W miejscu gdzie powstaje obraz rzeczywisty znajduje się krzyż nitek. Jeśli lunetka zostanie ustawiona na prążku zerowym, a następnie zostanie przesunięta na prążek widma, to kąt przesunięcia będzie równy kątowi ugięcia światła danej barwy. Pomiaru wielkości kąta dokonuje się za pomocą skali kątowej.

Najpierw ustawia się lunetkę na prążek zerowy. Na skali kątowej odczytujemy położenie prążka zerowego 0. Następnie przesuwamy lunetkę w lewo i ustawiamy na kolejnych prążkach pierwszego rzędu. Na skali kątowej odczytujemy położenia barw widma (od fioletowej-'1 do czerwonej-'7). Przesuwając dalej lunetkę odczytuje się wartości kąta ugięcia dla prążków widma drugiego rzędu (''1-''7). Wszystkie wyniki zapisywane są w tabelach 1 i 3, odpowiednio dla każdej z siatek.

Potem ustawiamy lunetkę znowu na prążku centralnym i odczytujemy jej położenie 0. Przesuwamy ją w prawo i odczytujemy wartości kąta ugięcia dla widm pierwszego i drugiego rzędu ('1-'7,''1-''7) wyniki tych pomiarów również notujemy w tabelach 1 i 3.

Po wykonaniu pomiarów wykonujemy obliczenia:

a) położenia kątowego prążków dyfrakcyjnych danej barwy względem prążka centralnego, po jego prawej i lewej stronie wg. wzorów i=|i0|, i=|i-0|.

=3°20'-35'=2°45', =1°25'-5'=1°30'.

b) średnie położenie kątowe prążków dyfrakcyjnych danej barwy i korzystając ze wzoru i= (i+i)/2.

1=(2°45'+1°30')/2=2°7'

c) błędy tych położeń i=|i-i|/2

1=|2°45'-1°30'|/2=37'

d) długość fali świetlnej odpowiadającej danej barwie 0x01 graphic
, gdzie k-rząd widma, a c-stała siatki

0x01 graphic

e) błąd długości fali 0x01 graphic

0x01 graphic

f) wartości dyspersji kątowej 0x01 graphic

0x01 graphic

Są to wyniki obliczeń dla prążka fioletowego I rzędu, który został uzyskany po przejściu światła przez siatkę dyfrakcyjną o stu rysach na mm.

Wyniki obliczeń zapisujemy w tabelach 2 i 4 odpowiednio dla każdej z siatek.

Tabela 1 (100 rys/mm)

0=35'

0=5'

Barwa

'

''

'

''

fioletowa

3°20'

6°00'

1°25'

4°00'

niebieska

3°25'

6°30'

1°40'

4°25'

zielona

4°5'

6°35'

2°00'

4°55'

żółta

4°15'

7°20'

2°15'

5°30'

pomarańczowa

4°20'

7°50'

2°25'

6°00'

czerwona 1

4°30'

8°00'

2°35'

6°10'

czerwona 2

4°50'

8°20'

2°40

6°35'

Tabela 2 (100 rys/mm)

Rząd widma

Barwa

[nm]

[nm]

D

[1/cm]

I

fioletowa

2°45'

1°30'

2°7'

37'

369

107

1000

II

fioletowa

5°25'

4°5'

4°45'

40'

414

58

2006

I

niebieska

2°50'

1°45'

2°17'

32'

398

93

1001

II

niebieska

5°55'

4°30'

5°12'

42'

453

61

2008

I

zielona

3°30'

2°5'

2°47'

42'

485

122

1001

II

zielona

6°20'

5°00'

5°40'

40'

493

58

2009

I

żółta

3°40'

2°20'

3°00'

40°

523

116

1001

II

żółta

6°45'

5°35'

6°10'

35'

537

50

2011

I

pomarańcz°

3°45'

2°30'

3°7'

37'

543

107

1001

II

pomarańcz°

7°15'

6°5'

6°40'

35'

580

51

2013

I

czerwony 1

3°55'

2°40'

3°17'

37'

572

107

1002

II

czerwony 1

7°25'

6°15'

6°50'

35'

594

50

2014

I

czerwony 2

4°15'

2°45'

3°30'

45'

610

130

1002

II

czerwony 2

7°45'

6°40'

7°12'

32'

626

46

2015

Tabela 3 (300 rys/mm)

0=40'

0=20'

Barwa

'

''

'

''

fioletowa

8°00'

15°40'

6°5'

13°15'

niebieska

8°40'

17°30'

7°15'

15°40'

zielona

9°15'

18°00'

7°40'

16°10'

żółta

10°35'

21°10'

9°00'

19°20'

pomarańczowa

11°10'

21°20

9°10'

19°35'

czerwona 1

11°20'

22°00'

9°30'

20°10'

czerwona 2

12°5'

24°00'

10°10'

22°5'

Tabela 4 (300 rys/mm)

Rząd widma

Barwa

[nm]

[nm]

D

[1/cm]

I

fioletowa

7°20'

6°25'

6°52'

27'

398

26

3021

II

fioletowa

15°00'

13°35'

14°17'

42'

411

20

6191

I

niebieska

8°00'

7°35'

7°47'

12'

451

11

3027

II

niebieska

16°50'

16°00'

16°25'

25'

471

12

6255

I

zielona

8°35'

8°00'

8°17'

17'

480

16

3031

II

zielona

17°20'

16°30'

16°55'

25'

485

11

6271

I

żółta

9°55'

9°20'

9°37'

17'

556

16

3042

II

żółta

20°30'

19°40'

20°5'

25'

572

11

6388

I

pomarańcz°

10°30'

9°30'

10°00'

30'

578

28

3046

II

pomarańcz°

20°40'

19°55'

20°17'

22'

577

10

6396

I

czerwony 1

10°40'

9°50'

10°15'

25'

593

24

3048

II

czerwony 1

21°20'

20°30'

20°25'

25'

581

11

6402

I

czerwony 2

11°25'

10°30'

10°57'

27'

633

25

3055

II

czerwony 2

23°20'

22°25'

22°52'

27'

647

12

6511

Sporządzamy we wspólnym układzie współrzędnych wykresy D=f() dla obu rzędów ugięcia.

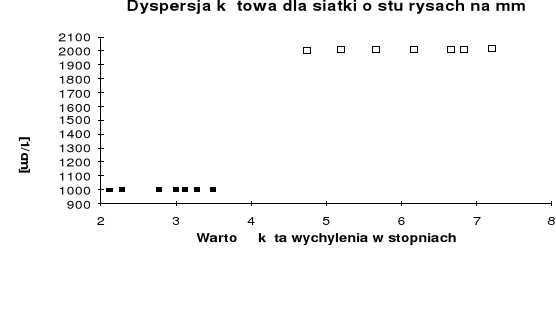
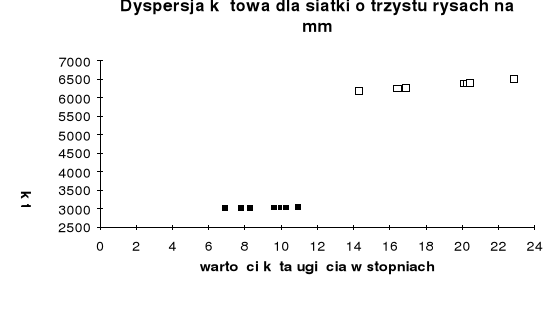
0x01 graphic

0x01 graphic

Wyznaczanie długości fali świetlnej za pomocą spektrometru siatkowego

2


Wyszukiwarka