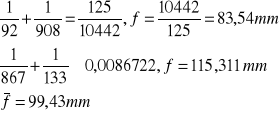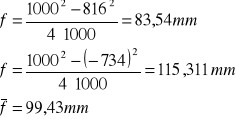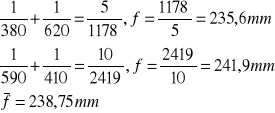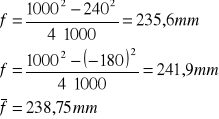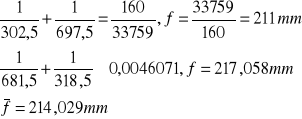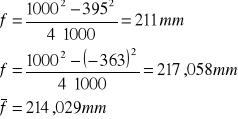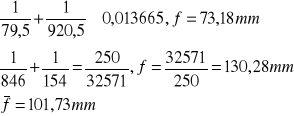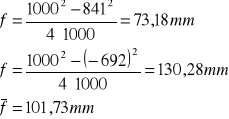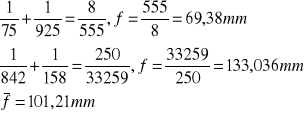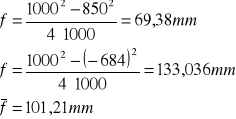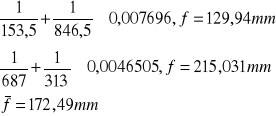Temat: Wyznaczanie ogniskowych soczewek ze wzoru soczewkowego oraz metodą Bessela

1. Soczewka to ciało przezroczyste ograniczone dwiema powierzchniami sferycznymi. Oś łącząca środki krzywizn obu tych powierzchni nazywamy osią optyczną soczewki. Światło przechodząc przez soczewkę ulega załamaniu kolejno na obu jej powierzchniach, promień przechodzący przez środek optyczny soczewki nie ulega załamaniu niezależnie od kąta padania na soczewkę. Wiązka promieni biegnąca równolegle do osi optycznej po przejściu przez soczewkę skupia się w jednym punkcie, nazwanym ogniskiem soczewki. Odległość między tym punktem, a środkiem soczewki nazywamy ogniskową soczewki.

Odpowiednie dobranie promień krzywizn powierzchni soczewki pozwala stworzyć soczewkę skupiającą, bądź rozpraszającą. W przypadku soczewek rozpraszających ogniskiem jest punkt przecięcia się przedłużeń promieni załamanych. Położenie ogniska zależy od współczynnika załamania materiału soczewki względem ośrodka, w którym się znajduje, a także od promieni krzywizn obu powierzchni ograniczających (R₁ i R₂).

Soczewki posiadają zdolność odwzorowywania punktów, polegającą na skupieniu promieni wybiegających z punktu P (przedmiotu), po przejściu przez soczewkę, w punkcie O (obraz), tworząc obraz przedmiotu. Położenie obrazu jest zależne od położenia przedmiotu oraz od ogniskowej soczewki i jest opisane tzw. Równaniem soczewkowym:

gdzie: p - odległość przedmiotu od soczewki, o - odległość obrazu od soczewki, f - ogniskowa.

Równanie to stosujemy gdy promienie wybiegające z P tworzą niewielki kąt z osią optyczną, soczewka ma małą grubość z porównaniu z R₁ i R₂. W stosunku do odległości p, o, f, R₁ i R₂ stosuje się następujące reguły mówiące o ich znaku:

• p jest zawsze dodatnie,

• o, R, f są dodatnie, gdy leżą po przeciwnej stronie soczewki niż przedmiot,

• o, R, f są ujemne, gdy leżą po tej samej stronie soczewki co przedmiot.

Na podstawie powyższego równania możemy w prosty sposób znaleźć ogniskową soczewki.

Możemy również obliczyć ogniskową soczewki metodą Bessela. Odległości o i p w powyższym równaniu występują w postaci symetrycznej, a więc po zamianie ich wartości równanie pozostanie prawdziwe. Konsekwencją tej symetrii jest możliwość uzyskania ostrego obrazu przy dwóch położeniach soczewki względem przedmiotu.

Przy stałej odległości l przedmiotu od ekranu obraz powstaje w odległości o oraz
o' = p od soczewki. W jednym położeniu obraz jest pomniejszony, a w drugim powiększony w stosunku do oryginalnego rozmiaru przedmiotu. Na podstawie tego możemy zapisać, że:

Po wyliczeniu z tych równań p i o, podstawieniu ich do pierwszego równania i kilku prostych przekształceniach otrzymujemy:

Aby wyznaczyć ogniskową z tego równania należy zmierzyć odległość przedmiotu od ekranu l oraz odległość e między dwoma położeniami soczewki, przy których obraz jest ostry.

3.

Na podstawie wzoru soczewkowego	Metoda Bessela
Soczewka A
Soczewka B
Soczewka C
Układ soczewek A4
Układ soczewek A5
Układ soczewek A6

4. Wnioski

Wielkość długości zwanej ogniskową soczewki możemy wyliczyć zarówno według równania soczewkowego, jak i według metody Bessela - w obu przypadkach wyniki są identyczne. Sama ogniskowa soczewki zależy od konkretnej soczewki, a dokładniej w tym przypadku od promieni krzywizn powierzchni sferycznych ograniczających soczewkę.

---