Rok akademicki 1997/98 |
Laboratorium z fizyki |
|||
Nr ćwiczenia: 55 |
Identyfikacja pierwiastka promieniotwórczego przez wyznaczenie górnej granicy widma beta
|
|||
Wydział: Elektronika Kierunek: I.K. |
TOMASZ SUCHOCKI |
|||
Data wykonania 1998-03-19 |
Ocena |
Data zaliczenia |
Podpis |
|
|
T |
|
|
|
|
S |
|
|
|
1. ZASADA POMIARU
Podczas rozpadu emitowane są dwie cząstki - cząstka (elektron) oraz neutrino lub antyneutrino. Energia rozpadu jest dzielona między te dwie cząstki, co tłumaczy fakt liniowości widma rozpadu:
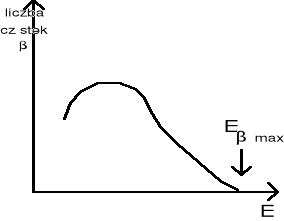
Widmo energetyczne cząstek β
Po ustawieniu na drodze cząstek absorbenta, można badać zależność między strumieniem cząstek, które przeszły określoną warstwę absorbenta i jego grubością. Maksymalny zasięg ![]()
mają cząstki o energii Ebmax , czyli powstałe w wyniku rozpadu, w którym cała energia przeszła na cząstkę -.
Znając zależność ![]()
= f(Ebmax) można określić energię Ebmax cząstek i zidentyfikować pierwiastek.
Maksymalny zasięg wyznacza się z prawa absorpcji cząstek :
![]()
gdzie:
![]()
- współczynnik masowy pochłaniania w cm2/g
R - grubość warstwy absorbenta w g/cm2
N0,N - strumień cząstek b w nieobecności i po przejściu absorbenta
Po wyznaczeniu ilości cząstek zarejestrowanych dla różnych grubości absorbenta, można wykreślić krzywą przy pomocy której przez ekstrapolcję do wartości tła otrzymujemy maksymalny zasięg cząstek . Teraz pozostaje tylko na jego podstawie ustalić rodzaj pierwiastka.
ln N = f(R)
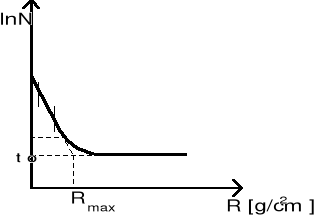
Krzywa absorpcji β
2. UKŁAD POMIAROWY
C
R
Układ pomiarowy do rejestracji cząstek β
3. OCENA DOKŁADNOŚCI POJEDYNCZYCH POMIARÓW:
ilość impulsów - licznik z wyświetlaczem cyfrowym zmiana ostatniej cyfry: 1
(1 impuls),
grubość folii - podana jako 20,25 mg/cm2, przyjmujemy za dokładną
4. TABELA POMIARÓW
L.p. |
ni |
ni |
Ni |
ilość |
Ri |
dNi |
lnNi |
d(lnNi) |
|
|
[imp / 100 sek] |
[imp / 100 sek] |
[imp / min] |
folii |
[g/cm2] |
|
|
|
|
1 |
187 |
|
|
0 |
0 |
|
|
|
|
2 |
190 |
189 |
113 |
0 |
0 |
11 |
4,73 |
0,09 |
|
3 |
128 |
|
|
1 |
0,02025 |
|
|
|
|
4 |
118 |
123 |
74 |
1 |
0,02025 |
9 |
4,30 |
0,12 |
|
5 |
89 |
|
|
2 |
0,0405 |
|
|
|
|
6 |
99 |
94 |
56 |
2 |
0,0405 |
8 |
4,03 |
0,13 |
|
7 |
63 |
|
|
3 |
0,06075 |
|
|
|
|
8 |
66 |
65 |
39 |
3 |
0,06075 |
6 |
3,66 |
0,16 |
|
9 |
50 |
|
|
4 |
0,081 |
|
|
|
|
10 |
55 |
53 |
32 |
4 |
0,081 |
6 |
3,45 |
0,18 |
|
11 |
31 |
|
|
5 |
0,10125 |
|
|
|
|
12 |
47 |
39 |
23 |
5 |
0,10125 |
5 |
3,16 |
0,21 |
|
13 |
32 |
|
|
6 |
0,1215 |
|
|
|
|
14 |
42 |
37 |
22 |
6 |
0,1215 |
5 |
3,10 |
0,21 |
|
15 |
32 |
|
|
7 |
0,14175 |
|
|
|
|
16 |
26 |
29 |
17 |
7 |
0,14175 |
4 |
2,86 |
0,24 |
|
17 |
25 |
|
|
8 |
0,162 |
|
|
|
|
18 |
29 |
27 |
16 |
8 |
0,162 |
4 |
2,79 |
0,25 |
|
19 |
31 |
|
|
9 |
0,18225 |
|
|
|
|
20 |
31 |
31 |
19 |
9 |
0,18225 |
4 |
2,92 |
0,23 |
|
tło |
30 |
30 |
18 |
9 |
0,182 |
4 |
2,89 |
0,24 |
|
5. ZESTAWIENIE WYNIKÓW
Odczytana z wykresu wartość maksymalnego zasięgu cząstek wynosi ok. 0,1 g/cm2. Na wykres naniesione zostały również proste, wykreślone pod największym i najmniejszym możliwym kątem, a więc wynikające z błędu ![]()
. Wartość odczytana z ich uwzględnieniem może wahać się w granicach: od 0,08 g/cm2 do 0,12 g/cm2. Maksymalna energia cząstek odczytana z wykresu zależności ![]()
od ![]()
wynosi ok. 0,4 MeV (wartość ta znajduje się bardzo blisko początku wykresu, dlatego trudno jest podać dokładną wartość dla ![]()
= 0,1 g/cm2 .
PIERWIASTEK |
|
14C |
0,155 |
45Ca |
0,255 |
185W |
0,430 |
32P |
1,704 |
89Sr |
1,500 |
204Tl |
0,783 |
Z danych podanych w tabeli możliwa jest dokładna identyfikacja pierwiastka. Najbardziej zbliżoną wartość ma wolfram 185W - o energii maksymalnej równej 0,430 MeV.
Maksymalny zasięg cząstek : 0,08 - 0,12 g/cm2
Maksymalna energia cząstek: 0,4 MeV
6. UWAGI I WNIOSKI
Do zliczania impulsów użyliśmy licznika cyfrowego, którego dokładność (zmiana ostatniej wyświetlanej cyfry) wynosiła 1 impuls. Średnie wartości ilości impulsów podane są w tabeli z zaokrągleniem do liczby całkowitej. Błąd statystyczny średniej z dwóch pomiarów liczony jest jako pierwiastek średniej:
![]()
Błąd bezwzględny wartości zlogarytmowanej, obliczony ze wzoru 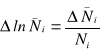
został naniesiony na wykres. Na wykresie została naniesiona prosta ekstrapolująca do wartości tła oraz proste możliwe do wykreślenia przy uwzględnieniu naniesionych błędów. Graficzny sposób prezentacji musiał mieć znaczący wpływ na dokładność wyniku. Z powodu korzystania kolejno z dwóch wykresów błędy wartości odczytanych z jednego nakładały się na błędy wartości odczytywanych z następnego. Na niedokładność końcowego wyniku miała wpływ rozbieżność na wykresie ln Ni = f(R) oraz mała dokładność początku wykresu ![]()
=f(Ebmax). Duży wpływ na błąd pomiaru miał także fakt, iż między foliami znajdowało się powietrze. Aby wyniki były prawidłowe grubość folii powinna stanowić całość, aby nie było między nią wolnych przestrzeni, w których znajdowałyby się inne pierwiastki mogące w pewnym stopniu absorbować promieniowanie.
6 Adam Harmuszkiewicz. Opracowanie doœwiadczenia 1995/1996 .
. 4
ZWN
PRZELICZNIK
Sonda
Licznika G-M
Wyszukiwarka