Mięsowicz Sławomir

1 CD L 6

Laboratorium Fizyczne

Temat laboratorium:

Wyznaczanie stałej siatki dyfrakcyjnej.

1. ZAGADNIENIA DO SAMODZIELNEGO OPRACOWANIA:

1. Światło jako fala elektromagnetyczna.

2. Interferencja fal świetlnych.

3. Zjawisko dyfrakcji fal.

II. WPROWADZENIE.

Jeżeli do jakiegoś punktu dociera równocześnie kilka ciągów fal, to punkt ten doznaje wychylenia będącego sumą wychyleń, wywołanych przez poszczególne ciągi fal. Zasadę tę nazywa się zasadą superpozycji. Szczególnym przypadkiem superpozycji jest interferencja. Warunkiem wystąpienia interferencji jest koherentność stykających się ciągów falowych. W przypadku fal świetlnych mogą interferować tylko ciągi fal wychodzące z tego samego punktu źródła światła, spotykając się po przebyciu różnych dróg w określonym punkcie.

W ośrodku jednorodnym zaburzenie wywołane przez źródło fal rozchodzi się w postaci fali z jednakową prędkością we wszystkich kierunkach. Zbiór punktów mających tę samą fazę drgań, tworzących powierzchnię ciągłą nazywamy powierzchnią fazową. W myśl zasady Huygensa wszystkie punkty czoła fali wysyłają równocześnie kuliste fale cząstkowe które rozchodzą się w przestrzeni. Zewnętrzna powierzchnia styczna do czół tych fal cząstkowych daje każdorazowo czoło fali rozchodzącej się w ośrodku. Prostą prostopadłą w każdym punkcie do czoła fali nazywamy promieniem fali. Połączenie zasady Huygensa z zasadą interferencji fal cząstkowych dokonane przez Fresnela nosi nazwę zasady Huygensa-Fresnela. Brzmi ona następująco: każdy punkt ośrodka w którym rozchodzi się fala jest źródłem fal cząstkowych, które wskutek interferencji dają falę obserwowaną. Zasadę tę można wykorzystać do wytłumaczenia zagadnienia prostoliniowego rozchodzenia się fali. Jeżeli na drodze promieniowania ustawimy przeszkodę, której rozmiary są mniejsze albo porównywalne z długością fali świetlnej, fala omija częściowo przeszkodę, uginając się na niej. Nie można w tym przypadku mówić o prostoliniowym rozchodzeniu się światła, zawodzi również pojęcie promienia.

Dyfrakcją nazywamy zjawisko uginania się fal świetlnych na krawędzi przeszkody i zachodzenia światła w obszar cienia geometrycznego. Jeżeli równoległą wiązkę światła po przejściu przez wąską szczelinę skierujemy przez soczewkę na ekran to powstanie na nim obraz dyfrakcyjny szczeliny w postaci jasnego środkowego maksimum i leżących po obu stronach minimów i maksimów oświetleni.

Siatką dyfrakcyjną nazywamy zbiór dużej liczby równoległych wąskich szczelin oddzielonych równymi nieprzeźroczystymi przerwami. Stałą siatki nazywamy sumę szerokości szczeliny i nieprzeźroczystej przerwy (d). Każda szczelina staje się źródłem fali cząstkowej. Rozpatrzmy wiązkę ugiętą pod kątem α. Maksima otrzymuje się gdy:

d sinα = kα k = 1, 2, . . . -rząd widma

Oprócz maksimów głównych występują maksima wtórne. Biorą się one z interferencji promieni w pewnej ilości szczelin i są widoczne w obszarach minimów oddzielających maksima

III. CEL ĆWICZENIA.

Ćwiczenie polega na wyznaczeniu stałej siatki dyfrakcyjnej tj. odległości między dwiema sąsiednimi szczelinami lub przesłonami. Wielkość tę oznaczamy d. Jeżeli różnica dróg optycznych dwu sąsiednich ugiętych promieni (wiązek) światła równa będzie całkowitej wielokrotności długości fali padającego światła - nakładające się wiązki ulegną wzmocnieniu. Warunkiem wzmocnienia jest spełnienie założenia: d sinα = kλ

gdzie:

λ - długość fali,

k - 0, 1, 2, 3, 4, ...

Zakładamy, że na siatkę pada fala płaska (co spełnia w przybliżeniu wiązka równoległa) światła monochromatycznego, które po przejściu przez siatkę ulega ugięciu. Ugięte fale pochodzące od sąsiednich szczelin nakładają się dając na ekranie maksimum w przypadku spełnienia warunku Δ=kλ

Interferencją fal nazywamy wzajemne nakładanie się fal o tej samej częstotliwości w danym ośrodku, prowadzące do wzmocnienia lub osłabienia (w zależności od różnicy faz fal składowych) natężenia fali wypadkowej.

0 - miejsce prążka zerowego, gdzie różnica dróg optycznych dla obu promieni wynosi 0

W miejscach oznaczonych +1 i -1 wiązki światła spełniają zależność:

d sinα = ±λ , α - jest to kąt pod jakim z punktu A widać odległość x pomiędzy prążkiem zerowym a prążkiem ugiętym (pierwszym). Przyjmując, że stała d jest niewielka w stosunku do x oraz y otrzymuje się warunek wzmocnienia obrazu interferencyjnego w postaci:

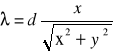
skąd po przekształceniu mamy:

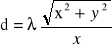
Jest to wzór określający stałą siatki.

4. WYKONANIE ĆWICZENIA

W skład układu pomiarowego wchodzi siatka dyfrakcyjna z dodatkowym układem optycznym (szczelina - soczewka) poprawiającym kolimację wiązki. Siatkę dyfrakcyjną oświetla się światłem pochodzącym z lampy sodowej, lasera He-Ne.

1. Zestawić układ optyczny według wskazówek prowadzącego.

2. Włączyć laser lampę sodowa zachowując ostrożność.

3. Ustawić siatkę dyfrakcyjną tak, aby na ekranie pojawił się ostry i dobrze widoczny obraz szczeliny.

4. Ustawić siatkę dyfrakcyjną jak najbliżej soczewki. Obserwować widoczne na ekranie prążki powstałe symetrycznie po obu stronach szczeliny.

5. Zmierzyć odległość między soczewką a ekranem (y), oraz odległość między zerowym a pierwszym prążkiem (x).

6. Pomiary wykonać dla prążków wyższych rzędów np.
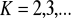
   mierząc odpowiednio x₂, x₃ ....

Kąt o jaki jest odchylana wiązka światła monochromatycznego na siatce dyfrakcyjnej wyliczyć ze wzoru:

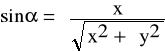
natomiast stałą siatki dyfrakcyjnej:

.

V. TABELKA POMIAROWA:

λ [nm]	K	x [cm]	Δx [cm]	y [cm]	Δy [cm]	sinα	d [nm]
590	2	4,7	0,1	21,9	0,1	0,210	5619,05
590	1	2,5	0,1	21,9	0,1	0,114	5175,44
590	0	0,0	0,1	21,9	0,1	1,000	-
590	1	-2,5	0,1	21,9	0,1	0,114	5175,44
590	2	-4,7	0,1	21,9	0,1	0,210	5619,05

Błąd w tym doświadczeniu obliczamy jako błąd średni korzystając z wzoru:

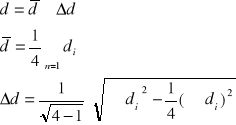
z obliczeń otrzymaliśmy: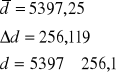

VI. WNIOSKI:

Z przeprowadzonych pomiarów i późniejszych obliczeń możemy stwierdzić, że stała badanej przez nas siatki dyfrakcyjnej ma wartość 5397±256,1 nanometrów.

Błąd jaki mógł mieć wpływ na wynik tego doświadczenia jest głównie błędem wykonujących pomiar, czyli błąd odczytu odległości między prążkami interferencyjnymi, a także pomiar odległości ekranu od siatki dyfrakcyjnej. Dokładność pomiaru tej wartości oceniliśmy na 0,1 cm. Dodatkowo wpływ na pomiar miała grubość prążków interferencyjnych która mogła wpłynąć na niedokładność pomiaru odległości między nimi.

Tego typu doświadczenie można by odwrócić i wykorzystać do pomiaru długości fali świetlnej spełniającej warunek koherentności. Należało by wtedy użyć siatki dyfrakcyjnej o znanej stałej, i korzystając z tych samych zależności wyznaczyć długość λ (która w naszym przypadku była znana i wynosiła 590 nanometrów).

4

5

---