8.Testy dla cech jakościowych:
TEST χ2: Karl Pearson w 1900 roku, dane zawarte w tabeli wielodzielczej, polega na porównaniu częstości zaobserwowanych z częstościami oczekiwanymi przy założeniu hipotezy zerowej (o braku związku między tymi dwiema zmiennymi).
Zastosowanie: cechy jakościowe w skali nominalnej, lub jakościowa z ilościową
1.H0: obie zmienne (cechy) są niezależne
H1: badane cechy są zależne, ich zależność nie jest przypadkowa.
2.Określamy poziom istotności, np. α = 0,05
3.Tworzymy tabelę asocjacji (kontyngencji), np., tabela czteropolowa - obie badane cechy dzielimy na 2 klasy, lub wielopolowe:
A |
B |
RAZEM |
|
|
I |
II |
|
I |
n11 = 8 |
n12 = 6 |
14 |
II |
n21 = 7 |
n22 = 5 |
12 |
RAZEM |
15 |
11 |
N = 26 |
4.Obliczamy wartości oczekiwane (teoretyczne) dla każdego z pól, czyli takie, które powinny być, gdyby rozkład liczebności w tabeli asocjacji był zgodny z odpowiednimi rozkładami brzegowymi. 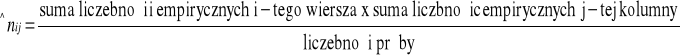
5.Tabelę asocjacji uzupełniamy wyliczonymi wartościami oczekiwanymi:
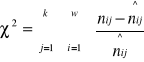
6.Obliczamy wartość statystyki χ2 według wzoru:
k - ilość kolumn w tabeli
w - ilość wierszy w tabeli
nij - wartości empiryczne, czyli zaobserwowane
n^ij - wartości oczekiwane (teoretyczne)
7.Znajdujemy w tablicach rozkładu χ2 wartość krytyczną χ2α dla poziomu istotności α przy df = (k-1)(w-1) stopniach swobody.
8.Wyliczoną wartość statystyki porównujemy z wartością krytyczną.
9.Podejmujemy decyzję:
10.nterpretujemy merytorycznie.
POPRAWKI DO TESTU χ2
LICZEBNOŚCI |
RODZAJ TESTU |
N>40 i wszystkie liczebności oczekiwane >10 |
Test χ2 |
N>40 i którakolwiek z liczebności oczekiwanych <10 |
Test V-kwadrat |
N>40 i którakolwiek z liczebności oczekiwanych <5 |
Test χ2 z poprawką Yates'a |
20<N≤40 i wszystkie liczebności oczekiwane >5 |
Test χ2 z poprawką Yates'a |
20<N≤40 i którakolwiek z liczebności oczekiwanych <5 |
Dokładny test Fisher'a |
N≤20 |
Dokładny test Fisher'a |
TEST McNEMARY: cechy jakościowe (dychotomicznych) prób powiązanych, jeżeli np. dwukrotny pomiar badanej cechy u tych samych jednostek, w międzyczasie wprowadzając jakieś działanie.
Określenie istotności różnic danych zależnych pomiędzy wynikami tych dwóch pomiarów.
SIŁA ZWIĄZKU:
Skala zależności pomiędzy cechami:
rxy=0 - zmienne nie są skorelowane
0,0 < rxy < - zależność nikła
0,1 ≤ rxy < 0,3 - zależność słaba
0,3 ≤ rxy < 0,5 - zależność przeciętna
0,5 ≤ rxy < 0,7 - zależność wysoka
0,7 ≤ rxy < 0,9 - zależność bardzo wysoka
0,9 ≤ rxy < 1 - zależność prawie pełna
Współczynnik Ф Yule'a: miara korelacji między dwoma zmiennymi jakościowymi w tabeli 2x2, Przyjmuje wartości z przedziału [0,1]., Nie informuje o kierunku zależności, tylko o sile zależności.
Współczynnik V-Cramer'a: miara korelacji między dwoma zmiennymi jakościowymi w tabeli 2x2, Przyjmuje wartości z przedziału [0,1], Nie informuje o kierunku zależności, tylko o sile zależności.
DO ZAGADNIENIA 2
Kierunek zależności:
Kierunek zależności między cechami można określić w przypadku współczynników korelacji, które zmieniają znak.
ξ > 0 - wzrost wartości jednej cechy powoduje również wzrost wartości drugiej cechy dla cech ilościowych
ξ < 0 - wzrost wartości jednej cechy powoduje spadek wartości drugiej cechy dla cech ilościowych.
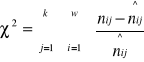
Wyszukiwarka