Zmienna losowa X - zmienna, która w wyniku pewnego doświadczenia przyjmuje z pewnym prawdopodobieństwem wartość z określonego zbioru - każda funkcja o wartościach liczbowych ze zbioru liczb rzeczywistych, która jest określona na zbiorze zdarzeń elementarnych
Zmienną losową X - nazywamy dyskretną (skokową), jeżeli zbiór wartości zmiennej X jest zbiorem skończonym lub przeliczalnym (ciąg liczbowy).
Zmienną losową X - nazywamy ciągłą, jeżeli zbiór wartości zmiennej X można przedstawić jako przedział liczbowy.
Zmienna losowa skokowa:
Rozkładem zmiennej losowej skokowej (funkcją rozkładu prawdopodobieństwa) nazywamy funkcję prawdopodobieństwa, która każdej realizacji zmiennej X przyporządkowuje określone prawdopodobieństwo:
![]()
, dla ![]()
gdzie:
P(X=xi) - prawdopodobieństwo, że zmienna X przyjmie wartość xi,
![]()
Dystrybuantą zmiennej losowej X nazywamy funkcję F(x) dla wszystkich liczb rzeczywistych o postaci
![]()
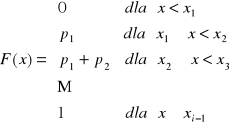
Wartość oczekiwana zmiennej losowej skokowej E(x):
![]()
Wariancja zmiennej losowej skokowej D2(X)
![]()
Zmienna losowa ciągła:
Funkcją gęstości prawdopodobieństwa zmiennej losowej ciągłej nazywamy funkcję f(x), określoną na zbiorze liczb rzeczywistych, spełniającą warunki:
![]()
dla każdego xR
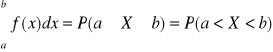
dla dowolnych a < b
Z powyższej definicji wynikają ważne własności funkcji gęstości:
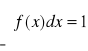
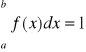
![]()
Dystrybuantą zmiennej losowej ciągłej nazywamy funkcję
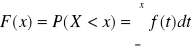
Na podstawie dystrybuanty zmiennej losowej ciągłej można obliczyć prawdopodobieństwa:
![]()
![]()
![]()
Wartość oczekiwana zmiennej losowej ciągłej
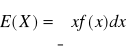
Wariancja zmiennej losowej ciągłej
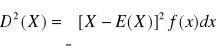
Wyszukiwarka