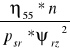Dane |
Obliczenia |
Wyniki |
ES = 0,000025 m ei = - 0,00005 m EI = 0 m es = - 0,000025 m
Lmax = 0,000075 m Lmin = 0,000025 m d = 0,04 m
n = 750 [obr/min] d = 0,04 [m]
vobw = 1,57 [m/s]
ψorient = 0,00084 ψśr = 0,0013
F = 5600 [N] d = 40 [mm] L = 40 [mm] pdop = 15 [MPa] |
ŁOŻYSKO ŚLIZGOWE
DANE: H7/f7 F = 5600 [N] n = 750 [obr/min] ES = 0,025 mm d = 40 [mm] L = d EI = 0 mm L = 0,06 m es = - 0,025 mm Fa = 0 [N] ei = - 0,05 RZC = 0,0016 [mm] RZP = 0,0032 [mm] pdop = 15 [MPa] αp = 23*10-6 [1/K] αc = 11*10-6 [1/K] β = Π
Lmax = ES - ei Lmax = 0,000075 m Lmin = EI - es Lmin = 0,000025 m
ψmax =
ψmin =
ψśr =
vobw = d*Πn vobw = 1,57 [m/s]
ψorient = 0,8*10-3*
Warunek dotyczący pasowania jest spełniony.
pśr = pdop = 15 * 106 [Pa] pśr ≤ pdop
Warunek na docisk jest spełniony.
|
Lmax = 0,000075 m Lmin = 0,000025 m
ψmax = 0,0019
ψmin = 0,0004
ψśr = 0,0013
vobw = 1,57 [m/s]
ψorient = 0,00084
pśr = 3,5 * 106 [Pa]
pdop = 15 * 106 [Pa] |
w = 1,4 m/s
L = 0,04 m d = 0,04 m
L0 = 0,354 m
tOt = 20 [°C] tBO = 55 [°C]
Dmax = 0,040025 m dmin = 0,03998 m d = 0,06 m dt = 35 [°C] αp = 23*10-6 [1/K] αc = 11*10-6 [1/K]
Dmin = 0,04 m dmax= 0,03995 m
n = 750 [obr/min] ψrz = 0,0016 pśr = 3,5 * 106 [Pa]
Ψrz = 0,0016
μ = 0,00504 F = 5600 [N] vobw = 1,57 [m/s]
NT = 44,31168 W A = 0,065 m2 αwnik = 20,796
d = 0,04 m ψrz = 0,0016
RZC = 0,0000011 m RZP = 0,0000021 m |
VG150
tBO = 55 [°C] w = 1,4 [m/s]
αwnik = 9,81* (0,7+1,2
AK = 27*L*d AK = 0,043 m2
AW = 0,5*L0*Π*d AW = 0,022 m2
A = Aw + Ak A = 0,065 m2
dt = tB0 - 20[°C] dt = 35 [°C]
Dmax = d + ES Dmax = 0,040025 m Dmin = d + EI Dmin = 0,04 m dmin = d + ei dmin = 0,03998 m dmax = d + es dmax= 0,03995 m
ψmaxtB = ψmaxtB = 1,546*10-3
ψmintB = ψmintB = 1,67*10-3
ψśr1 = (ψmaxtB + ψmintB)/2 ψśr1 = 0,0016
ψrz = ψśr1
η55 = 60 * 10-3 [Pa*s]
S =
μ = Ψrz* 3,15 (3,15 - zależność Sommerfelda) μ = 0,00504
NT = μ*F*vobw NT = 44,31168 W
tB =
ε = 1 - 0,51
h0 = 0,5 * Π * d * (1 - ε) * Ψrz h0 = 0,0000493 m
RZC + RZP = 0,0000032 m
h0 = 0,0000493 m
RZC + RZP < h0
Warunek jest spełniony.
|
tBO = 55 [°C ] w = 1,4 [m/s]
αwnik = 20,796 [
AK = 0,043 m2
AW = 0,022 m2
A = 0,065 m2
dt = 35 [°C]
Dmax = 0,060025 m Dmin = 0,04 m dmin = 0,03998 m dmax= 0,03995 m
ψmaxtB = 1,546*10-3
ψmintB = 1,67*10-3
ψśr1 = 0,0016
S = 5,02
μ = 0,00504
NT = 44,31168 W
tB = 32,46°C
h0 = 0,0000493 m |
Wyszukiwarka