Rachunek różniczkowy funkcji jednej zmiennej

1. Obliczyć z definicji pochodną podanej funkcji we wskazanym punkcie:

a)
,
; b)
,

2. Zbadać różniczkowalność funkcji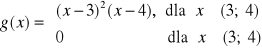
.

3. Stosując reguły różniczkowania obliczyć pochodne funkcji:

a)
b)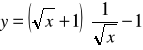
c)

d)
e)
f)

g)
h)
i)

j)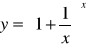
k)

4. Napisać równanie stycznej do podanej krzywej:

)
w punkcie

)
w punkcie

)
w punkcie

)
prostopadłej do prostej
.

5. Napisać wzór Taylora dla funkcji
, gdy
.

6. Przy pomocy wzoru Taylora obliczyć liczbę e z dokładnością do
.

7. Oszacować dokładność podanych wzorów przybliżonych:

a)
, dla

, dla

8. Wyznaczyć przedziały wypukłości i punkty przegięcia wykresu funkcji:

a)
b)
c)

9. Obliczyć wskazane granice:

a)
b)
c)

d)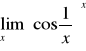
e)
.

10. Znaleźć wartość c, o której mówi twierdzenie Rolle'a dla funkcji
w przedziale
.

11. Znaleźć c, o którym mowa w twierdzeniu Lagrange'a dla funkcji
w
.

12. Zbadać monotoniczność funkcji:

a)
b)
c)

13. Znaleźć ekstrema funkcji:

a)
b)
c)

14. Zbadać przebieg funkcji i naszkicować jej wykres:

a)
b)
c)

d)
e)
.

15. Znaleźć najmniejszą i największą wartość wielomianu
na przedziale
.

16. Wyznaczyć najmniejszą i największą wartość funkcji
na przedziale
.

17. Podać promień podstawy stożka o największej objętości jaki można wpisać w sferę o promieniu R.

18. Liczbę 120 podzielić na dwie części tak, aby iloczyn jednej z tych części przez kwadrat drugiej był największy.

---