1. Sigma σ-algebry zdarzeń - w przestrzeni Ω nazywamy rodziną F jej podzbiorów spełniającą następujące aksjomaty:
1) Ω ∈ F,
2) jeżeli A ∈ F, to A'∈ F (A'=Ω\A)
3) jeżeli A1, A2 ∈ F, to ![]()
Ai ∈ F
Elementy σ-algebry zdarzeń F nazywamy zdarzeniami losowymi zdarzeniami.
2. Aksjomatyczna definicja prawdopodobieństwa.
Jeżeli Ω jest przestrzenią zdarzeń elementarnych, F jest σ-algebrą zdarzeń, to prawdopodobieństwo nazywamy funkcją. p: F→R, taka że:
1) dla każdego A∈F jest P(A)≥0
2) P(Ω)=1 (wartość unormowania)
3) jeżeli A1, A2, .... jest dowolnym ciągiem parami wykluczających się zdarzeń, to:
P(![]()
Ai)=![]()
(Ai)
3.Własności prawdopodobieństwa.
1) P(∅)=0
2) jeżeli A⊂B, to P(A) ≤ P(B)
3) P(A∪B) = P(A) + P(B) - P(A∩B)
4) P(A∪B) ≤ P(A) + P(B)
5) jeżeli B⊂A, to P(A\B) = P(A) - P(B)
6) P(A\B) = P(A)-P(A∩B)
7) P(A') = 1 - P(A)
4. Definicja przestrzeni probabilistycznej. Trójka (Ω, F, P)
5. Definicja prawdopodobieństwa warunkowego.
Prawdopodobieństwo zdarzenia A pod warunkiem zdarzenia B określone jest wzorem:
P(A\B)=![]()
, P(B)>0
6.Definicja zdarzeń niezależnych.
Mówimy, że zdarzenia A i B SA niezależne jeżeli: P(A∩B) = P(A)∙ P(B).
Jeżeli zdarzenia A i B są niezależne i P(B)>0, to P(A\B)=P(A)
Mówimy, że zdarzenia A1, A2, … (ciąg skończony lub nieskończony) są niezależne, jeżeli dla dowolnych Ai1, Ai2, …, Aik zachodzi równość:
P(Ai1 ∩ Ai2 ∩…∩ Aik) = P(Ai1) x P(Ai2) x … x P(Aik)
Uwaga. Jeżeli wszystkie lub tylko niektóre zdarzenia niezależne A1, A2, … zastąpimy przez zdarzenia przeciwne do nich, to otrzymamy również zdarzenia niezależne.
7.Definicja zmiennej losowej.
Niech (Ω,F,P) będzie dowolną przestrzenią probabilistyczna. Zmienna losową X nazywamy funkcją określoną na przestrzeni zdarzeń elementarnych Ω i przyjmującą wartości rzeczywiste: X: Ω→R, spełniającą warunek: {ω: X(ω)≤x} ∈ F, dla każdego x∈R
8.Definicja i własności dystrybuanty.
Dystrybuantą zmiennej losowej X nazywamy funkcją rzeczywistą zmiennej rzeczywistej określona wzorem:
F(x)=P({ω: X(ω)≤x}) = P(X ≤ x), dla każdego x∈R
Twierdzenie. Funkcja F(x) jest dystrybuantą pewnej zmiennej losowej ↔ :
1) F(x) jest niemalejąca,
2) F(x) jest prawostronnie ciągła
3) ![]()
F(x)=0
4) ![]()
F(x)=1
(WYKRESY)
9.Własności dystrybuanty:
P(X ≤ a) = F(a)
P(X < a) = ![]()
F(x) = F(a-)
P(X = a) = F(a) - F(a-)
P(X > a) = 1 - F(a)
P(X ≥ a) = 1 - F(a-)
P(a < X ≤ b) = F(b) - F(a)
P(a < X < b) = F(b-) - F(a)
P(a ≤ X ≤ b) = F(b) - F(a-)
P(a ≤ X < b) = F(b-) - F(a-)
10. Definicja i własności wartości oczekiwanej.
Własności:
1) Wartość oczekiwana jest operatorem liniowym, tzn.
E(aX + By) = aEX + bEY, a, b ∈ R
2) Jeżeli zmienne losowe X i Y są niezależne, to
E(X∙Y) = EX ∙ EY
3) Jeżeli h(x) jest funkcja przedziałami ciągłą, to
E[h(x)] = 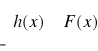
, gdzie F(x) jest dystrybuantą zmiennej losowej x.
11. Definicja i własności wariancji.
Wariancją zmiennej losowej X nazywamy liczbą D2X określoną wzorem: D2X = E(X-EX)2
Wariancją jest miara rozrzutu. Interpretacja fizyczna: moment bezwładności względem środka masy.
Własności wariancji:
1) D2X ≥ 0
2) D2X = 0 ↔ zmienna losowa X przyjmuje wartość stałą z prawdopodobieństwem 1,
tzn. gdy P(x=x0) = 1 dla pewnej liczby x0 ∈ R
3) D2(aX + b) = a2 ∙ D2X, a, b ∈ R
4) Jeżeli X I Y są niezależne, to:
D2(X + Y) = D2X + D2Y
5) D2X = EX2 - (EX)2
12. Definicja i własności rozkładu wykładniczego.
Rozkład wykładniczy to rozkład zmiennej losowej opisujący sytuację, w której obiekt może przyjmować stany X i Y, przy czym obiekt w stanie X może ze stałym prawdopodobieństwem przejść w stan Y w jednostce czasu. Prawdopodobieństwo wyznaczane przez ten rozkład to prawdopodobieństwo przejścia ze stanu X w stan Y w czasie δt.
Własności:
1) Gęstość:
-rozkład wykładniczy jednoparametrowy o parametrze λ (λ > 0):
f(x) = λeλxI[0,∞](x)
-rozkład wykładniczy ujemny (dwuparametrowy) z parametrami położenia μ ∈ R
i parametrami skali σ > 0 ma gęstość:
f(x; μ, σ) = ![]()
I(μ,∞)(x)
-rozkład podwójnie wykładniczy o parametrach położenia β i parametrze skali γ > 0
ma gęstość:
f(x; β, γ) = ![]()
, x ∈ R
2) Dystrybuanta jest funkcją F określoną dla wartości rzeczywistych x taką, że
F(x) = P(X < x). Dla ciągłej zmiennej losowej X:
F(x) = 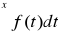
,
gdzie f jest gęstością X.
3) Wariancją zmiennej losowej X jest wielkość będąca miarą rozproszenia rozkładu
wokół wartości oczekiwanej. Zazwyczaj stosuje się oznaczenia: Var(X), D2(X), σ2
Jeżeli EX < ∞, to Var(X) = EX2 - (EX)2
13. Definicja i własności rozkładu normalnego.
Istnieje wiele równoważnych sposobów zdefiniowania rozkładu normalnego. Należą do nich: funkcja gęstości, dystrybuanta, momenty, kumulanty, funkcja charakterystyczna, funkcja tworząca momenty i funkcja tworząca kumulanty. Wszystkie kumulanty rozkładu normalnego wynoszą 0 oprócz pierwszych dwóch.
Własności:
1) Jeżeli zmienne losowe x1, x2, …, xn są niezależne oraz x ~ N(μi; σi) i=1, 2, …
x1 + x2 +… +xn ~ N(μ1, μ2, …+ μn) ![]()
2) Jeżeli zmienne losowe x1, x2, …, xn są niezależne oraz
xi ~ N(μ, σ) dla i=1,2,…,n
x1 + x2 +…+xn ~ N(n μ, σ![]()
)
3) Jeżeli zmienne losowe x1 i x2 są niezależne oraz
x1 ~ N(μ1,σ1) x2 ~ N(μ2,σ2)
to x1 - x2 x1 ~ N(μ1- μ2,![]()
)
4) Jeżeli zmienne losowe x1, x2 są niezależne oraz
x1 ~ N(μ,σ) x2 ~ N(μ,σ)
to x1 - x2 ~ N(0, ![]()
σ)
5) Jeżeli zmienne losowe x1, x2,…, xn są niezależne oraz
xi ~ N(μ1,σ1) dla i=1,2,…
to ![]()
n =![]()
~ N(![]()
(μ1 + μ2 +…+ μn)∙![]()
(![]()
))
6) Jeżeli zmienne losowe x1, x2,…, xn są niezależne
xi ~ N(μ,σ) dla i=1,2,…,n
![]()
n =![]()
~ N(μ,![]()
)
14. Definicja estymatora niedociążonego.
Estymator ![]()
n parametru Q nazywamy estymatorem zgodnym, jeżeli
![]()
P(|![]()
n - Q| < ε) = 1 dla każdego ε > 0
Estymator ![]()
n, który przy każdym n spełnia warunek E![]()
n = 0 nazywamy estymatorem niedociążonym parametru Q.
Jeżeli ![]()
E![]()
n =Q, to estymator ![]()
n nazywamy estymatorem asymptotycznie niedociążonym parametru Q.
15. Definicja estymatora najefektywniejszego.
Estymator niedociążony, którego wariancja jest możliwie najmniejsza nazywamy estymatorem najefektywniejszym parametru Q. Miara efektywności niedociążonego estymatora ![]()
n jest liczba: ef![]()
n = 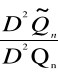
Zwaną efektywnością estymatora ![]()
n, gdzie ![]()
jest estymatorem najefektywniejszym.
0 < ef![]()
n ≤ 1
Jeżeli ef![]()
n = 1, to estymator ![]()
n jest najefektywniejszy.
Jeżeli ![]()
ef![]()
n = 1, to ![]()
n nazywamy estymatorem asymptotycznym najefektywniejszym parametru Q.
16. Definicja przedziału ufności.
Przedziałem ufności (dwustronnym) dla parametru Q na poziomie ufności 1- α, α ∈ (0;1), nazywamy przedział (Q*, Q*) spełniający warunki:
- jego końce są statystykami,
- P(Q* < Q < Q*) = 1 - α
(q*, q*) - realizacja przedziału ufności
Odp. Przedział (q*, q*) z prawdopodobieństwem 1 - α pokrywa nieznany parametr Q.
17. Definicja hipotezy statystycznej.
Hipotezę statystyczną nazywamy każde przypuszczenie dotyczące nieznanego rozkładu badanej cechy populacji, które może być zweryfikowane na podstawie sporawej próby.
Hipotezę dzielimy na:
- parametryczne,
- nieparametryczne
Hipotezę podlegającą weryfikacji nazywamy hipotezę zerową i oznaczamy H0. Każda dopuszczalna hipoteza poza hipotezą zerową nazywa się hipotezą alternatywną i oznacza się
H1.
18.19. Definicja błędu I rodzaju i błędu II rodzaju:
Sprawdzając hipotezę statystyczną możemy podjąć poprawną decyzję albo popełnić jeden z dwóch następujących błędów:
- możemy odrzucić weryfikowaną hipotezę H0, wtedy gdy jest ona w rzeczywistości prawidłowa (błąd I rodzaju, prawdopodobieństwo jego popełnienia oznaczamy przez α).
- możemy przyjąć weryfikowaną hipotezę H0, jako prawidłową, podczas gdy jest ona w rzeczywistości fałszywa (błąd II rodzaju, prawdopodobieństwo jego popełnienia oznaczamy przez β).
Obydwa błędy są ze sobą sprzężone, jeżeli opieramy się na tej samej próbie, to mniejsze α pociąga za sobą większe β i na odwrót).
20. Definicja obszaru krytycznego.
R - zbiór wartości statystyki testowej Un, których wystąpienie jest tak mało prawdopodobne, gdy hipoteza H0 jest prawdziwa, że odczytujemy je jako zaprzeczenie hipotezy H0 (obszar krytyczny).
21. Od czego zależy obszar krytyczny.
Obszar krytyczny zależy od:
- rozkładu statystyki testowej,
- postaci hipotez,
- prawdopodobieństw błędów.
22. Definicja poziomu istotności.
Test, w którym bierzemy pod uwagę jedynie prawdopodobieństwo α popełniania błędu i rodzaju nazywamy testem istotności, a prawdopodobieństwo α nazywamy poziomem istotności.
23. Definicja mocy testu.
Prawdopodobieństwo odrzucenia hipotezy H0, gdy prawidłowa jest hipoteza H1 nazywamy mocą testu.
moc testu = 1 - β
W klasycznej teorii weryfikacji hipotez statystycznych przy ustalonym poziomie istotności α, statystykę i obszar krytyczny dobieramy tak, aby możliwie największa była moc testu.
24. Typy decyzji weryfikowanych dla hipotez.
Typy decyzji weryfikacji przy ustalonym poziomie istotności α:
- Jeżeli Un ∈ R, to odrzucamy hipotezę H0, z prawdopodobieństwem błędu i rodzaju równym α,
- Jeżeli Un ∉ R, to nie ma podstaw do odrzucenia hipotezy H0, z prawdopodobieństwem 1 - α.
25. Definicja zmiennej losowej dwuwymiarowej.
Niech (Ω,F, P) będzie dowolną przestrzenią probabilistyczną. Zmienną losową dwuwymiarową (X, Y) nazywamy funkcję:
(X, Y): Ω → R2
Niezależną względem σ -algebry zdarzeń F, tzn. spełniającej warunek:
![]()
{ω ∈ Ω: X(ω) ≤ x, Y(ω) ≤ y} ∈ F
(X,Y) - dwuwymiarowe zmienne losowe
x,y - jednowymiarowe zmienne losowe
26. Definicja i własności dystrybuanty zmiennej losowej dwuwymiarowej.
Funkcję F: R2 → <0;1> określoną wzorem F(x, y) = P(X ≤ x, Y ≤ y), dla (x, y) ∈ R2 nazywamy łączna dystrybuanty zmiennej losowej dwuwymiarowej (X, Y).
Uwaga:
P(X ≤ x, Y ≤ y) = P({ω: X(ω) ≤ x} ∩ {ω: Y(ω) ≤ y})
27. Definicja niezależności zmiennych losowych.
Mówimy, że zmienne losowe X i Y SA niezależne, jeżeli:
![]()
F(x, y) = Fx(x) ∙ Fy(y)
Zmienne losowe skokowe X i Y SA niezależne, jeżeli
![]()
Pij = Pi ∙ Pj
Zmienne losowe absolutnie ciągłe X i Y są niezależne, jeżeli
![]()
f(x, y) = fx(x) ∙ fy(y)
28. Definicja i własności kowariancji.
Kowariancją zmiennych losowych X i Y nazywamy liczbę
cor(X,Y) = E[(X - EX)(Y - EY)]
Własności kowariancji:
1) cor(X,Y) = D2X
2) cor(X,Y) = cor(Y,X)
3) cor(X,Y) = E(X ∙ Y) - EX ∙ EY
4) (cor(X,Y)) ≤ σx ∙ σy nierówność Schwarza
29. Definicja macierzy kowariancji.
Macierz kowariancji:
![]()
= 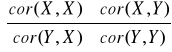
Korzystając z własności kowariancji mamy:
![]()
=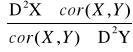
Macierz kowariancji jest macierzą symetryczna.
30. Definicja i własności współczynnika korelacji.
Współczynnikiem korelacji Pearsona nazywamy liczbę
δ = ![]()
, σx,σy > 0
Własności współczynnika korelacji:
1) -1 < δ < 1
2) | δ| = 1 ⇔ istnieją takie stałe a, b ∈ R, a≠0, że P(Y= aX + b) = 1
3) Jeżeli X i Y SA niezależnymi zmiennymi losowymi, to δxy = 0
4) δxx = 1
5) δxy = δyx
![]()
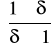
macierz współczynnika korelacji
C - macierz symetryczna
31. Definicja zmiennych losowych nieskorelowanych.
Współczynnik korelacji Pearsona mierzy siłę zależności liniowej zmiennych losowych X i Y. Mówimy, że zmienne losowe X i Y są nieskorelowane jeżeli δxy = 0
32. Definicja linii regresji I rodzaju.
Zbiór punktów spełniających równanie:
y = E(Y|X = x)
nazywamy linią regresji I rodzaju zmiennej losowej Y względem zmiennej losowej X.
33. Definicja linii regresji II rodzaju.
Punkcje g(x) nazywamy funkcją regresji II rodzaju zmiennej losowej Y względem zmiennej losowej X, jeżeli wyrażenie:
E{[Y - u(X)]2}
Przyjmuje wartość minimalną dla u(x) ≡ g(x), gdy u(X) należy do ustalonej klasy funkcji.
34. Definicja i interpretacja współczynnika determinacji.
Współczynnik determinacji jest jedną z podstawowych miar jakości dopasowania modelu. Informuje o tym, jaka część zmienności zmiennej objaśnianej została wyjaśniona przez model. Jest on więc miarą stopnia, w jakim model wyjaśnia kształtowania się zmiennej objaśnianej. Można również powiedzieć, ze współczynnik determinacji opisuje tę część zmienności zmiennej objaśnianej, która wynika z jej zależności od uwzględnionych w modelu zmiennych objaśniających. Współczynnik determinacji przyjmuje wartości z przedziału [0;1]. Jego wartości najczęściej są wyrażane w procentach. Dopasowanie modelu jest tym lepsze, im jego wartość jest bliższa jedności.
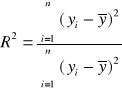
gdzie:
yi - rzeczywista wartość zmiennej objaśnianej
ŷi - wartość teoretyczna zmiennej objaśnianej (na podstawie modelu)
![]()
- średnia arytmetyczna empirycznych wartości zmiennej objaśnianej
35. Własności dwuwymiarowego rozkładu normalnego.
Zmienna losowa (X, Y) ma dwuwymiarowy rozkład normalny, jeśli ma gęstość postaci:
f(x, y) = 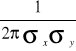
∙ exp 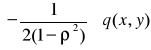
,
gdzie:
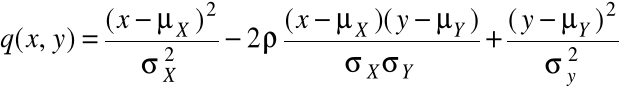
- ∞ < x < ∞, - ∞ < y < ∞, stałe σx, σy, ρ spełniają warunki σx > 0, σy > 0, -1 < ρ < 1
(X, Y) ~ N(μx, μy, σx, σy, ρ)
Jeśli (X, Y) ~ N(μx, μy, σx, σy, ρ), to:
1) X ~ N(μx, σx), Y ~ N(μy, σy)
2) cor(X, Y) = ρ
3) X, Y są niezależne ⇔ ρ = 0
Wyszukiwarka