2. Tw. o trzech siłach:

Trzy nierównoległe do siebie działające w jednej płaszczyźnie pozostają w równowadze wtedy i tylko w tedy gdy tworzą układ zbieżny a ich kierunki tworzą trójkąt zamknięty. P₁=P₂+P₃

3. Tw. Varignona:

Suma momentów sił układu zbieżnego względem dowolnego punktu jest równa momentowi wypadkowej tego układu względem punktu ∑ⁿ_i=1r∙∑P_i=r∙W

4. Para sił:

Układ dwóch sił równoległych P' = −P, P' = P nie leżących na jednej prostej nazywamy parą sił. Odległość między siłami nazywamy ramieniem pary sił.

Aby pary sił działające w jednej płaszczyźnie na ciało sztywne znajdowały się w równowadze, suma momentów tych par musi

się równać zeru.

5. Moment sił względem punktu: Mo=r∙F

Moment sił względem osi: M=r∙P , moment ten jest wektorem swobodnym do płaszczyzny π czuli ma kierunek prostej l

10. Kinematyczne równania ruchu:

x=x(t). y=y(t). z=z(t)

11. Prędkość

v=lim Δr/Δt = dr/dt = r' prędkość zawsze jest styczna do toru i zawsze jest wektorem v=x'i+y'j+z'k v=√(x')²+(y')²+(z')²

12. Przyspieszenie

a=lim Δv/Δt = dv/dt = r'' przyspieszenie nigdy nie jest styczne do toru chyba że jest linią prostą v=x''i+y''j+z''k v=√(x'')²+(y'')²+(z'')²

13. Przyspieszenie styczne i normalne:

a_s=dv/dt - przyspieszenie styczne

a_n=v²/ρ - przyspieszenie normalne

14. Droga: s= _t1∫^t2Vdt

18. Rodzaje ruchów bryły sztywnej:

l. ruch postępowy - to taki ruch w którym dowolna prosta sztywno związana z tą bryłą zajmuje położenie wzajemnie równoległe (3 stopnie swobody).

2. ruch obrotowy - to taki ruch bryły w którym dowolne dwa punkty bryły są nieruchome, prosta przechodząca przez dwa punkty to oś obrotu (1 stopień swobody).

3.ruch płaski - to taki ruch bryły w którym dowolny przekrój tej bryły płaszczyzną zajmuje położenie równoległe i jest równoległy do pewnej stałej płaszczyzny zwanej kierującą (3 stopnie swobody).

4. ruch kulisty - to taki ruch bryły w którym bryła porusza się dookoła nieruchomego punktu bryły (3 stopnie swobody).

5. ruch ogólny -jest to złożenie ruch postępowego i kulistego.

19 . Ruch postępowy bryły sztywnej:

v=dr_o/dt=v_o a=d²r_o/dt²=dv_o/dt=a_o

- wszystkie punkty bryły sztywnej w ruchu postępowym mają te same prędkości v_o i przyśpieszenia a_o w tej samej chwili czasu.

- tory wszystkich punktów bryły mają ten sam kształt.

- dla opisu ruchu postępowego bryły wystarczy podać równanie ruchu jednego punktu bryły, np. początku ruchomego układu współrzędnych O'.

20 . Ruch obrotowy bryły:

ω=dφ/dt ε=dω/dt=d²φ/dt² v=ω×r' a=ε×r'+ω×(ω×r')

a=ε×r'+ω(ω∙r')-ω²r'

21. Prędkość kątowa:

Prędkość kątowa jest równa kątowi zakreślonemu podczas ruchu podzielonemu przez czas.

22. Przyspieszenie kątowe, ε, wielkość pseudowektorowa charakteryzująca zmiany prędkości kątowej ω bryły sztywnej lub punktu materialnego.

Przyspieszenie kątowe określone jest równaniem:

23. Prędkość liniowa punktu, a prędkość kątowa bryły.

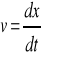
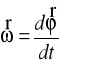
24. Prędkość i przyspieszenie bryły w ruchu płaskim.

v=v_o+ω×r' a=a_o+ε×r'+ω(ω∙r')-ω²r'

25. Twierdzenie o rzutach prędkości dwóch punktów bryły poruszającej się ruchem płaskim.

Tw. o trzech rzutach - jeśli bryła znajduje się w ruchu płaskim to rzuty prędkości 2 dowolnych punktów A i B na łączące je proste są równe.

Taki punkt należący do bryły lub leżący poza nią który w pewnej chwili ma prędkość 0 nazywa się chwilowym środkiem obrotu (punkt C). Przy pomocy chwilowego środka obrotu możemy znaleźć prędkość punktów posługując się wzorem v=ω×CA. Wektor prędkości kątowej jest zawsze taki sam i jest jeden dla wszystkich punktów bryły.

26. Chwilowy środek obrotu.

Patrz 25.

33. Ruch złożony punktu.

34. Prędkość bezwzględna

Prędkość w ruchu obrotowym unoszenia

Prędkość w ruchu względnym (prostoliniowym )

36. Przyspieszenie Coriolisa.

Przyspieszenie Coriolisa równe jest podwojonemu iloczynowi wektorowemu prędkości kątowej układu ruchomego i prędkości względem punktu A. p_c=2ω×v_r. Przyspieszenie Coliolisa nie występuje gdy ruchem unoszenia są ruchy: prostoliniowy, harmoniczny prosty i postępowy (ၷ= zero),gdy wektor prędkości kątowej jest równoległy do wektora prędkości względnej oraz gdy prędkość względna jest równa zeru.

37. Zasady Newtona.

I prawo bezwładności: punkt materialny, na który nie działa żadna siła lub działające siły się równoważą, pozostaje w spoczynku lub porusza się ruchem jednostajnym po linii prostej.

II prawo: przyśpieszenie punktu materialnego jest proporcjonalne do siły działającej na ten punkt i ma kierunek taki jak ta siła. F=ma.

III prawo akcji i reakcji: siły wzajemnego oddziaływania dwóch punktów materialnych mają jednakowe wartości, leżą na prostej łączącej te punkty i są przeciwnie skierowane.

IV prawo zasady superpozycji: jeżeli na punkt materialny działa jednocześnie kilka sił, to każda z nich działa niezależnie od pozostałych, a wszystkie razem działają jak jedna siła równa wektorowej sumie danych sił.

V prawo powszechnego ciążenia: Każde dwa punkty materialne o masach m₁ i m₂ przyciągają się z siłą wprost

proporcjonalną do iloczynu ich mas i odwrotnie proporcjonalną do kwadratu odległości r między nimi. Kierunek siły leży na prostej łączącej te punkty. F=k m₁m₂/r²

38. Zasada d'Alemberta.

Suma sił rzeczywistych i siły bezwładności działających na punkt materialny jest w każdej chwili równa zeru.

F+(-ma)=0

39. Zasada zachowania pędu; 40. Zasada pędu i popędu.

Pędem punktu materialnego o masie m i prędkości v nazywamy iloczyn masy punktu i jego prędkości: p=mv

Zasada pędu: Pochodna względem czasu pędu układu punktów materialnych jest równa wektorowi głównemu sił zewnętrznych działających na ten układ. ma=F ; a=dv/dt → m dv/dt=F ; m=const. d/dt (mv)=F → dp/dt=F.

Zasada pędu i popędu (lub inaczej, prawo zmienności pędu) Przyrost pędu układu materialnego w skończonym przedziale czasu jest równy popędowi wektora głównego sił zewnętrznych działających na ten układ. p(t)-p(0)=∫^t₀Fdt

Zasada zachowania pędu: jeżeli wektor główny układu sił zewnętrznych działających na ten układ materialny jest równy zeru, to pęd tego układu materialnego jest stały: dp/dt=F; F=0; dp/dt=0; p=const.

41. Zasada zachowania krętu: jeżeli moment główny sił zewnętrznych względem nieruchomego punktu redukcji O jest równy zeru, to kręt układu materialnego (bryły) względem tego punktu jest wielkością stałą. Jeżeli M_o=0 to k₀=const.

42. Zasada krętu: pochodna względem czasu krętu układu punktów materialnych względem dowolnego nieruchomego punktu jest równa momentowi głównemu wszystkich sił zewnętrznych względem tego samego punktu. dk_o/dt=M_o

43. Dynamiczne równania ruchu punktu materialnego.

a=dv/dt e_s +v²/ρ e_n

e_s=m dv/dt

e_n=m v²/ρ

e_b=e_s×e_n

57. Drgania swobodne.

Drgania swobodne mx''=-kx ; ω²=k/m → x''+ ω²x=0

x=Asinω_ot gdzie. x-wychylenie ciała z położenia równowagi w chwili czasu t, A - amplituda drgań, ω - częstość kołowa drgań. Brak tłumienia i brak wymuszenia.

58. Drgania tłumione.

Drgania tłumione mx''+βx'+kx=0 ; x''+β/m x'+k/m x=0 ; β/m = 2u ; k/m=ω²

Drgania słabo tłumione(u<ω).Okres drgań jest dłuższy od okresy drgań nie tłumionych zachodzących pod działaniem takiej samej siły sprężystej. Drgania tłumione nie są drganiami periodycznymi. Drgania silnie tłumione (u>ω) drgania tłumione są drganiami aperiodycznymi dla tych drgań wychylenie maleje wykładniczo z czasem. Tłumienie krytyczne (u=ω).

59. Logarytmiczny dekrement tłumienia.

wielkość charakteryzująca tłumienie drgań, zdefiniowana jako logarytm naturalny stosunku amplitud dwóch kolejnych wychyleń w tę samą stronę drgającej cząsteczki.

60. Drgania wymuszone mx''+kx=Hsinpt gdzie p- częstość kołowa siły wymuszającej, H- amplituda wymuszenia;

x''+k/m x=H/m sinpt; x''+ω²x=hsinp

p<ω - wówczas przesunięcie fazowe dąży do 0 i mówimy że częstość siły wymuszającej jest zgodna w fazie z siłą wymuszającą

p>ω - przesunięcie fazowe dąży do -π i wychylenia drgań harmonicznych zależy od masy ciała wykonującego drgania

p=ω - przesunięcie fazowe dąży do π/2 i zachodzi zjawisko rezonansu.

61. Rezonans.

zjawisko fizyczne zachodzące dla drgań wymuszonych, objawiające się pochłanianiem energii poprzez wykonywanie drgań o dużej amplitudzie przez układ drgający dla określonych częstotliwości drgań.

62. Amplituda.

największa wartość A₀ osiągana przez wielkość fizyczną A, zmieniającą się w czasie t w sposób harmoniczny, tj. proporcjonalnie do sin (ωt+ϕ₀), gdzie ω - częstotliwość kątowa, ϕ₀ - początkowa faza drgań.

63. Okres drgań.

dla ruchu periodycznego czas, po jakim układ drgający znajduje się ponownie w takiej samej fazie.

64. Częstotliwość drgań.

Częstotliwość drgań to liczba cykli wykonywanych przez drgające środowisko w ciągu jednej sekundy. Częstotliwość określa się w hercach (Hz)

66. Faza drgań.

Dla drgań harmonicznych opisanych równaniem

fazą drgań określa się argument funkcji sinus, czyli

lub resztę z dzielenia tego kąta przez miarę kąta pełnego

Faza jest wyrażana w jednostkach kąta, zwykle w układzie SI w radianach.

Kąt φ nazywa się fazą początkową drgań, czyli fazą w chwili początkowej t = 0.

---