Ćwiczenie 10
Tomasz Zaborny , gr.8
Wyznaczanie modułu Younga metodą zginania pręta
Wprowadzenie
Jeśli na unieruchomione ciało sprężyste podziałamy siłą, to powstaną w tym ciele naprężenia, wywołujące jego odkształcenie. Naprężenie σ w pręcie o przekroju poprzecznym A, na który działa siła F ( prostopadła bądź styczna do A ) równe jest stosunkowi siły do pola powierzchni przekroju pręta :
σ = F / A
Naprężeniu stawiają opór siły międzycząsteczkowe wewnątrz materiału. Rozróżnia się zwykle trzy rodzaje naprężeń : rozciągające - wywołujące wydłużenie ciała, ściskające - powodujące kurczenie ciała i ścinające - deformujące postać.
Zmiana długości pręta spowodowana rozciąganiem lub ściskaniem jest proporcjonalna do jego długości. Jeśli na przykład pręt o długości l, rozciągany siłą F, zwiększa swoją długość o Δl, to miarą odkształcenia![]()
jest względna zmiana długości :
![]()
=Δl / l
Gdy po usunięciu siły F ciało wraca do swych wymiarów, to odkształcenie nazywamy sprężystym. Dla małych odkształceń sprężystych ![]()
jest proporcjonalne do naprężenia σ :
![]()
,
gdzie E jest modułem sprężystości danego materiału ( nazywanym też modułem Younga ). Moduł Younga wyraża się, podobnie jak naprężenie czy ciśnienie, w paskalach: 1Pa = 1N/ m2
Liniowa zależność pomiędzy naprężeniem a odkształceniem znana jako prawo Hooke'a.
Prawo Hooke'a stwierdza, że podczas rozciągania lub ściskania zmiana długości jest proporcjonalna do działającej siły
![]()
,
Najprostszy sposób wyznaczenia modułu Younga polega na pomiarze przyrostu długości Δl pręta o długości l i przekroju A, umocowanego jednym końcem i rozciąganego siła F. Jednak w przypadku grubszych prętów trudno jest uzyskać ich mierzalne wydłużenia, z uwagi na konieczność użycia bardzo dużych sił. Z tego względu wykorzystujemy odkształcenia złożone, do których należy zginanie pręta umocowanego z jednej strony lub podpartego na obu końcach.
Wykonanie zadania
Badany pręt kładziemy na specjalnych podporach umieszczonych na podstawie stojącej na stole. Strzemię T nakładamy na środek pręta i zawieszamy na nim szalkę. Do pomiaru strzałki ugięcia stosujemy śrubę mikrometryczną umocowaną w specjalnym statywie. Mikromierz ustawiamy nad strzemieniem tak, aby koniec śruby nie dotykał do strzemienia. Do zacisków, które znajdują się na strzemieniu i na statywie śruby mikrometrycznej, podłączamy szeregowo zasilacz 6V i odpowiednią żaróweczkę. Przez obracanie śruby mikromierza doprowadzamy ją do zetknięcia ze strzemieniem. Gdy żaróweczka rozbłyśnie, odczytujemy wskazanie mikromierza - s0. Obciążamy szalkę - ugięcie pręta przerywa obwód i żrówka gaśnie. Ponownie obracamy śrubę, aż do momentu zaświecenia żarówki i odczytujemy wskazanie mikromierza - s1. Różnica S1 = s1 - s0 daje strzałkę ugięcia S1. Pomiary strzałek ugięcia Si przeprowadzamy dla kilku różnych obciążeń Pi , przy czym najpierw notujemy strzałki ugięcia przy obciążeniach rosnących, a następnie malejących. Z dwóch uzyskanych wyników dla danej wartości obciążenia obliczamy wartość średnią, którą przyjmujemy jako wartość średnią, którą przyjmujemy jako właściwą wartość strzałki ugięcia.
Na podstawie wyników uzyskanych dla różnych obciążeń obliczamy średnią wartość P / S. Jeśli wprowadzimy oznaczenie dla pojedynczego pomiaru : ![]()
oraz dla wartości średniej ![]()
, to możemy ją wyrazić następująco :
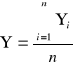
,
n - liczba różnych odłożeń pręta.
Pomiar rozmiarów pręta
Jako długość l przyjmujemy odległość pomiędzy krawędziami podpór, na których spoczywa pręt - mierzymy ja linijką. Następnie dodatkową śruba mikrometryczną mierzymy krawędzie przekroju poprzecznego pręta ai i hi - w wielu różnych miejscach pręta, poczym wyliczamy wartości średnie a i h. Otrzymane wartości pozwalają wyznaczyć stałą pręta C :
![]()
Rodz. Pręta |
Dług. [m] |
Szerokość ai [mm] |
Sred. a |
Grubość hi [mm] |
Sred. h |
C [m-1] |
||||
Drewno |
0,945 |
30,1 |
29,9 |
29,7 |
29,86 |
10,00 |
10,60 |
10,10 |
10,21 |
6,63 *106 |
|
|
30,05 |
29,7 |
30,05 |
|
10,10 |
10,50 |
10,10 |
|
|
|
|
29,55 |
30,00 |
29,7 |
|
9,9 |
10,10 |
10,50 |
|
|
Metal |
0,945 |
19,8 |
20,2 |
19,8 |
20,03 |
5,05 |
4,9 |
4,9 |
4,91 |
8,88 *107 |
|
|
20,2 |
20,2 |
20,2 |
|
4,9 |
4,9 |
4,9 |
|
|
|
|
19,8 |
19,9 |
20,2 |
|
4,9 |
4,9 |
4,85 |
|
|
Obliczanie modułu Younga
Iloczyn stałej pręta C i średniej wartości Y stosunku P do S daje wartość modułu Younga dla danego pręta o przekroju prostokątnym :
E=C*Y
Metal : E=C*Y=8,88*107*2,22=19,71*107
Drewno : E=C*Y=6,63*106*2,38=15,7*106
Rodzaj pręta |
Masa ob.[kg] |
Wskazania mikrom. [mm]przy obciążeniu |
Śr.strz. Ugięcia Si [m] |
Pi / Si [N / m] |
Srednia Y=P/S |
Moduł Younga E [Pa] |
|
|
|
rosnącym |
Malejąc. |
|
|
|
|
Metal
|
0 |
24,74 |
24,74 |
|
|
2,22 |
19,71 *107 |
|
0,10 |
24,28 |
24,30 |
0,45 |
2,27 |
|
|
|
0,20 |
23,85 |
23,87 |
0,88 |
2,27 |
|
|
|
0,30 |
23,40 |
23,43 |
1,32 |
2,27 |
|
|
|
0,40 |
22,97 |
22,99 |
1,76 |
2,25 |
|
|
|
0,50 |
22,52 |
22,55 |
2,20 |
2,23 |
|
|
|
0,60 |
22,10 |
22,12 |
2,41 |
2,41 |
|
|
|
0,70 |
21,66 |
21,70 |
3,06 |
2,27 |
|
|
|
0,80 |
21,22 |
21,22 |
3,52 |
2,27 |
|
|
Drewno
|
0 |
24,48 |
24,45 |
|
|
2,38 |
15,7 *106 |
|
0,05 |
24,25 |
24,23 |
0,22 |
2,24 |
|
|
|
0,10 |
24,05 |
24,03 |
0,42 |
2,31 |
|
|
|
0,15 |
23,18 |
23,82 |
0,65 |
2,34 |
|
|
|
0,20 |
23,60 |
23,67 |
0,83 |
2,42 |
|
|
|
0,25 |
23,44 |
23,48 |
1,00 |
2,51 |
|
|
|
0,30 |
23,23 |
23,27 |
1,21 |
2,43 |
|
|
|
0,35 |
23,03 |
23,07 |
1,41 |
2,48 |
|
|
|
0,40 |
22,87 |
22,87 |
1,51 |
2,61 |
|
|
Rachunek błędów
Dla metalu :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
n(n-1)=72
![]()
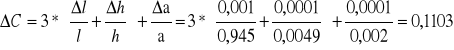
![]()
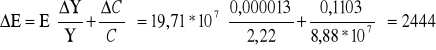
![]()
Dla drewna :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
n(n-1)=72
![]()
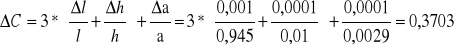
![]()
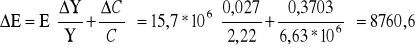
![]()
Wyszukiwarka