Oprocentowanie - określenie przyszłej wart. pieniądza na podst. znanej wart. aktualnej.

Dyskontowanie - określenie bż wart. pieniądza na podst. znanej wart. przyszłej.

Dyskonto matematyczne (rzeczywiste proste) - od aktualnej (nieznanej) wart. kapitału na podst. obowiązującej stopy proc. r: D_M=K₀r

Dyskonto handlowe - od przyszłej (znanej) wart. kapitału na podst. przewidywanej stopy proc. d (s.dyskontowej) D_H=K₁r; D_H=K_n*d_*n

Roczna stopa dyskonta - stosunek dyskonta handlowego do kwoty należnej wierzycielowi po upływie roku.

Odsetki Z= K₁-K₀ = FV-PV:

- wyrażają się jedn. pieniężnych (wielkość mianowana),

- są miarą bezwzględną przyrostu wart. kapitału,

Stopa proc. - miara względna, niemianowana tempa wzrostu wart. kapitału r=Z/K₀

Okres konwersji (kapitalizacji) - czas po którym odsetki dopisywane są do kapitału T_k­.

Kapitalizacja: prosta (oprocentowaniu podlega wyłącznie kap.początkowy), złożona (cały kapitał), z dołu (dopisywanie na koniec okresów), z góry (na początku), zgodna (odsetki dopisywane w okresach równych okresowi nominalnej stopy proc. T_k=T, niezgodna (w różnych okresach T_k~T_s)

Kapitalizacja w podokresach - okres stopy proc. jest całkowitą wielokrotnością okresu kapitalizacji (np.: kap. kwartalna - m=4)

Kapitalizacja w nadokresach - okres kapit. jest całkowitą wielokrotnością okresu stopy proc. (np.: trzyletnia - m=1/3)

TWIERDZENIA DOT. KAPITALIZACJI:

1. Wart. przyszła kapitału K₀ w modelu kapit. prostej nie zależy od okresu kapit.

2. Dla dowolnej, ustalonej wielokrotności okresu stopy proc. przyszła wart. K₀ w złożonej z dołu jest rosnącą f. częstości kapit. (dla dowolnych l. naturalnych n i m K_n=K_n/1<=K_n*n/m)

3. […] w złożonej z góry jest malejącą f. częstości kapit. (W_n*n/m<=W_n/1=W_n oraz K_n<=K_n*n/m<= W_n*n/m<= W_n)

Efektywna stopa proc. r_ef­^d w złożonej z dołu - stopa roczna dla której K_n(r_ef­^d)=K_nm/m(r/m). Równoważy efekt kapit. w podokresach przez zwiększenie stopy nom. (rocznej).

Równoważna stopa proc. r_r^d - stopa odniesiona do okresu kapital. T_k, dla której K_n(r)=K_nm/m(r_r^d). Równoważy efekt kapital. w podokresach poprzez zwiększenie stopy dostosowanej r/m do wart. r_r^g

Wysokość stóp procentowych i równoważnych nie zależy od n-liczby lat (tzn. l. okresów stopy proc.)

Stopy efektywne mają ten sam okres T_s co stopa nominalna r (niwelują skutki kapitalizacji niezgodnej).

Stopy równoważne mają ten sam okres T_k co stopa dostosowana r/m (równoważą efekt kapit. niezgodnej).

EFEKTYWNA STOPA PROC. DLA KAPIT. CIĄGŁEJ r_ef=e^r-1

Przeciętna stopa proc. - stopa r_prz, przy której przyszła wart. kapitału K₀ po n-okresach stopy proc. jest taka sama, jak przy zmieniającej się stopie proc.

Wkłady oszczędnościowe (renta) - systematyczne wpłaty podlegające dalej oprocentowaniu zgodnie z przyjętym modelem kapitalizacji, a także ratalna spłata zaciągniętej pożyczki oraz ciąg opłat za użytkowanie czegoś.

Okres wpłat wkładów oszczędnościowych T_w - czas pomiędzy kolejnymi wpłatami.

Wartość sumy wkładów zależy od:

• modelu kapitalizacji odsetek;

• wzajemnych relacji pomiędzy okresem stopy procentowej Ts, okresem kapitalizacji Tk i okresem wkładów Tw. Jeżeli okresy te są równe to wkłady oszczędnościowe nazywać będziemy zgodnymi, w przeciwnym wypadku niezgodnymi.

OPROCENTOWANIE PROSTE WKŁADÓW OSZCZĘDNOŚCIOWYCH

WKŁADY ZGODNE

T_s=T_k=T_w

WKŁADY NIEZGODNE

• T_s≠T_w

• 
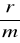
  -względna stopa procentowa o okresie równym okresowi wkładów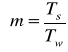
  

OPROCENTOWANIE ZŁOŻONE WKŁADÓW OSZCZĘDNOŚCIOWYCH

WKŁADY ZGODNE

• T_s=T_k=T_w

• q=1+r, r jest okresową stopą procentową.

WKŁADY NIEZGODNE - przynajmniej dwa spośród trzech okresów są różne

OKRES WKŁADÓW RÓWNY OKRESOWI KAPIT.

• T_k=T_w≠ T_s

• 
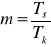
  częstość kapitalizacji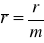

• 
  względna stopa procentowa o okresie równym okresowi kapitalizacji (uzgodnienie wkładów polega na przyjęciu nowego okresu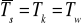
  )

• 
  

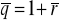
OKRES WKŁADÓW WIĘKSZY OD OKRESU KAPIT. (Kapit. częstsza niż wkłady)

• 
  ,
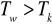
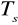
  - dowolny (np. wkłady półroczne, kapitalizacja kwartalna)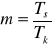

• 
  częstość kapitalizacji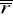

• 
  - stopa procentowa dostosowana do okresu wkładów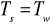
  

• uzgodnienie wkładów polega na wprowadzeniu stopy efektywnej
  

• 
  

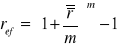
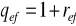
OKRES WKŁADÓW MNIEJSZY OD OKRESU KAPIT. (wkłady częstsze niż kapit)

• 
  ,
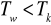
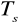
  - dowolny (np. wkłady miesięczne przy kapitalizacji kwartalnej)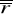

• 
  - stopa procentowa dostosowana do okresu kapitalizacji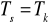
  

• wkładów dokonywano przez n okresów kapitalizacji, przy czym w każdym okresie kapitalizacji dokonywano m wkładów o tej samej wysokości E. Łączna liczba wkładów jest równa nm.

Rentą kapitałową - systematyczny dochód uzyskiwany ze zgromadzonego wcześniej kapitału rentowego.

Definicja2

Okres wypłat T_w jest to czas pomiędzy dwiema kolejnymi wypłatami.

Renty (ze względu na wysokość wypłat):

1. - Renty stałe (kolejne wypłaty renty są stałe)

2. - Renty zmienne - stosowana jest w związku z istniejącą na rynku inflacją, zwiększające się wysokości wypłat mają zapewnić utrzymanie wartości realnej otrzymywanych kwot

1. - Renty arytmetyczne (ciąg wypłat, których wysokość zmienia się (na ogół rośnie) o jednakową kwotę)

2. - Renty geometryczne (ciąg wypłat, których wysokość zmienia się (na ogół rośnie) w jednakowym stosunku)

RENTA STAŁA ZGODNA

• T_w =T_s=T_k

• r - nominalna stopa procentowa o okresie T_s, q=1+r

• e - stała wysokość renty wypłacanej przez n okresów (z dołu bądź z góry)

Renta wieczysta - renta, której wysokość nie przekracza wartości odsetek, tzn.
.

Maksymalna renta wieczysta wypłacana z kapitału rentowego K:

• 
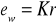
  - z dołu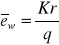

• 
  - z góry

Renta czasowa - jeśli wartość renty stałej przekracza wysokość renty wieczystej, pomniejsza kapitał rentowy i jest wypłacana przez skończony okres.

Równanie
określa wyzerowanie konta.

RENTA STAŁA NIEZGODNA - spośród trzech okresów T_k, T_w, T_s przynajmniej dwa są różne

OKRES WPŁAT RÓWNY OKRESOWI KAPIT.

• T_w=T_k, T_s - dowolny

• uzgodnienie renty polega na dostosowaniu okresu stopy procentowej do okresu wypłat i okresu kapitalizacji:
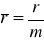
  - stopa względna;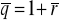
  

Zastosowanie stopy względnej
pozwala na równoważne zastąpienie renty niezgodnej rentą zgodną.

OKRES WYPŁAT WIĘKSZY OD OKRESU KAPIT.

• T_w>T_k, T_s - dowolny (np. renta półroczna przy kapitalizacji miesięcznej)

• T_s dostosowujemy do okresu wypłat

• uzgodnienie renty polega na równoważnym wydłużeniu okresu kapitalizacji, tak aby był równy okresowi stopy procentowej
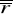
  (dostosowanej do okresu wypłat) i okresowi wypłat.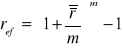

• 
  , m - oznacza ile razy w okresie wypłat odsetki są dopisywane do kapitału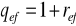

• 
  

OKRES WYPŁAT MNIEJSZY OD OKRESU KAPIT.

• T_w<T_k, T_s - dowolny (np. renta wypłacana miesięcznie przy kapitalizacji półrocznej)

T_s dostosowujemy do okresu kapitalizacji

(MODEL KAPITALIZACJI ZŁOŻONEJ Z DOŁU)

• uzgodnienie renty polega na zastąpieniu kapitalizacji okresowej wg stopy procentowej
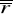
  na kapitalizację w podokresach, zgodnie z okresem wypłat, wg stopy równoważnej: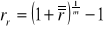
  ;
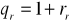
  ; m - liczba określająca ile razy okres kapitalizacji jest większy od okresu wypłat

(MODEL KAPITALIZACJI MIESZANEJ)

• odsetki za okres kapitalizacji wyznaczane wg modelu kapitalizacji złożonej z dołu

• odsetki za okresy wypłat renty wyznaczane wg modelu kapitalizacji prostej

• n - liczba pełnych okresów kapitalizacji

• m - liczba wypłat w każdym okresie kapitalizacji

• uzgodnienie renty polega na zastąpieniu m wypłat renty e w podokresach okresu kapitalizacji jedną umowną wypłatą z dołu E, równoważną w sensie równej wartości końcowej zgodnie z modelem kapitalizacji prostej

RENTA ARYTMETYCZNA ZGODNA

• T_w =T_s=T_k

• r - nominalna stopa procentowa o okresie T_s, q=1+r

• e - stała wysokość renty wypłacanej przez n okresów (z dołu bądź z góry)

• kolejne wypłaty renty tworzą ciąg arytmetyczny o różnicy d, czyli ciąg: e, e+d, e+2d, …

RENTA GEOMETRYCZNA ZGODNA

• T_w =T_s=T_k

• r - nominalna stopa procentowa o okresie T_s, q=1+r

• e - stała wysokość renty wypłacanej przez n okresów (z dołu bądź z góry)

• kolejne wypłaty renty tworzą ciąg geometryczny o ilorazie a, czyli ciąg: e, ea, ea², …

RENTA KAPITAŁOWA Z UWZGLĘDNIENIEM INFLACJI

• W czasie wypłacania renty zarówno stopa procentowa r oraz stopa inflacji i są stałe.

• Okres stopy procentowej r jest taki sam jak okres stopy inflacji i.

• q=1+r

• p=1+i

---