Podstawowe operatory języka Matlab:

• = operator przypisania

np. :

c=1

• [ , , ; , , ] konstrukcja macierzy i tablic

np.:

a=[ 1 2 3;2 4 3]

tworzy macierz :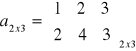

`SPACJA' lub `,' oddzielają elementy tego samego wiersza a `;' kolejne wiersze, tak stworzona tablica musi mieć jednakową ilość elementów we wszystkich wierszach. Macierze można budować z innych macierzy np.:

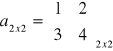
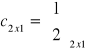
d=[a c;b]

• min:max tworzenie wektora o elementach od `min' do `max' co 1

np.:

b=1:3

tworzy wektor b=[1 2 3]

• min:kr:max tworzenie wektora o elementach od `min' do `max' z krokiem `kr'

np.:

b=0:0.1:1

tworzy wektor b=[0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1]

• m(w,k) wybór elementów z macierzy `m' o indeksach z przecięcia `w' wierszy i `k' kolumn

np.:

a(1,2)

wybiera z macierzy a element o indeksie 1x2

a(1:3,[2 4])

wybiera z macierzy a element z przecięcia wierszy 1,2,3 z kolumnami 2,4

a(2,:)

wybiera z macierzy a element całego wiersza 2

Podstawowe funkcje języka Matlab:

Elementarne funkcje macierzowe.

• zeros(w,k) generuje macierz złożoną z samych zer o `w' wierszach i `k' kolumnach

• ones(w,k) generuje macierz złożoną z samych jedynek o `w' wierszach i `k' kolumnach

• eye(w,k) generuje macierz jednostkową o `w' wierszach i `k' kolumnach

• rand(w,k) generuje macierz złożoną z elementów pseudolosowych z zakresu 0-1 o `w' wierszach i `k' kolumnach

np.:

a=ones(2,3)

b=eye(3)

funkcje mogą być też jednoargumentowe jeśli tworzymy macierze kwadratowe, jak w przykładzie

Podstawowe operatory algebraiczne

• operatory macierzowe

+ dodawanie macierzy

- odejmowanie macierzy

* mnożenie macierzowe

/ mnożenie przez odwrotność macierzy

^ mnożenie macierzy przez siebie

' transpozycja macierzy

np.:

a=[1 2 3;3 2 4]; b=[1 3;1 2];

c=a*b

d=a/b

e=b^2

• operatory tablicowe

.* mnożenie elementów tablic przez siebie

./ dzielenie elementów tablic przez siebie

.^ potęgowanie elementów tablicy

np.:

a=[1 2 3;3 2 4]; b=[1 3 2;1 2 3];

c=a.*b

d=a./b

e=a.^2

f=a.^b

Podstawowe operatory logiczne

• operatory relacji

== równe

~= różne

< mniejsze

> większe

<= mniejsze równe

>= większe równe

np.:

a==1

• funktory logiczne

& AND iloczyn logiczny

| OR suma logiczna

~ NOT negacja logiczna

xor( , ) XOR różnica symetryczna

np.:

a=[0 1 0 1] & [0 0 1 1]

Podstawowe funkcje

• funkcje trygonometryczne

sin()

cos()

tan()

asin()

acos()

atan()

• funkcje różne

sqrt() √

pow2() 2^x

exp() e^x

log() ln()

log2() lg₂()

log10() log()

abs() | moduł |

• funkcje zaokrąglenia i działania na liczbach całkowitych

round() zaokrąglenie

ceil() zaokrąglenie => +∞

floor() zaokrąglenie -∞ <=

fix() zaokrąglenie =>0 <=

sign() zwraca znak -1,0,1

rem( , ) reszta z dzielenia

gcd( , ) największa wspólna dzielna

lcm( , ) najmniejsza wspólna wielokrotność

Podstawowe konstrukcje programistyczne

• instrukcja warunkowa IF

if wyrażenie_warunkowe

elseif wyrażenie_warunkowe

else

end

np.:

if x<0

disp('x jest liczbą mniejszą od 0')

elseif x>0

disp('x jest liczbą większą od 0')

else

disp('x wynosi 0')

end

• pętla WHILE

while wyrażenie_warunkowe

end

np.:

i=1;

while i~=0

i=i-0.2;

disp(i);

end

• pętla FOR

for i=[...]

end

np.:

for i=[1 3 4]

disp(i);

end

wyświetli na ekranie:

1

3

4

Podstawowe funkcje interakcji z użytkownikiem.

• num2str() zamienia liczbę na ciąg znaków

• str2num() zamienia ciąg znaków na liczbę

• disp() wyświetla na ekranie dane

np.:

disp(a)

disp(['wynik obliczeń = ', num2str(obl)])

• input() pozwala na wprowadzenie danych z klawiatury przez użytkownika

np.:

a=input('Podaj wartość początkową: ')

pozwala na zapamiętanie w zmiennej `a' wartości liczbowych wpisanych przez użytkownika

b=input('Podaj swoje imię: ','s')

pozwala na zapamiętanie w zmiennej `b' danych typu string wpisanych przez użytkownika

• pause zatrzymuje wykonywanie programu do chwili naciśnięcia dowolnego klawisza przez użytkownika

Skrypty i funkcje w Matlabie.

W Matlabie można wykonywać programy zapisane w postaci skryptów. Skrypty mogą zawie­rać obliczenia oraz konstrukcje programistyczne takie jak instrukcja warunkowa, pętla. Skrypty mają postać plików tekstowych zapisanych z rozszerzeniem *.m zapisanych w bieżą­cym katalogu (polecenie - cd) lub w ścieżce należącej do ścieżki przeszukiwań (polece­nie - path)

Program zawarty w skrypcie można uruchomić wpisując nazwę skryptu bez rozszerzenia w linii poleceń. Przykład skryptu zapisanego w pliku skrypt.m:

skrypt.m

a=input('Jak sie nazywasz ? ','s');

disp(['Hello ',a]);

disp('Teraz narysuję parabolę');

disp('Naciśnij dowolny klawisz...');

pause;

x=-3:0.1:3

y=x.^2-2.*x

plot(x,y);

grid on;

Oprócz typowych programów, można w postaci skryptów zapisać funkcje. W jednym pliku można zapisać tylko jedną funkcję. Nazwa pliku obligatoryjnie musi być zgodna z nazwą funkcji. W pierwszej linii skryptu musi się znaleźć definicja funkcji postaci:

function [wynik1 , wynik2 , ...] = nawa_funkcji (dana1 , dana2 , ...)

Przykład funkcji wyliczającej wartość wielomianu:

funkcja.m

function [y]=funkcja(x);

y=x.^4-8.*x.^2+1

Wywołanie takiej funkcji może nastąpić w skrypcie lub z linii poleceń i może mieć postać:

y=funkcja(2)

y1=funkcja(-4:0.5:3)

Polecenia umożliwiające tworzenie okien graficznych z wykresami funkcji.

W Matlabie zaimplementowano szereg funkcji do tworzenia grafiki dwu-
i trójwymiarowej. Wykorzystywane są one do graficznej ilustracji danych. Poniżej przedstawiono najczęściej stosowane polecenia służące kreśleniu funkcji:

• jednej zmiennej

plot(x,y,'typ_linii')

x - wektor określający przedział zmienności argumentów funkcji

y - wektor będący rozwiązaniem funkcji

typ_linii - parametr określający symbol koloru i rodzaju linii

Przykład m-pliku kreślącego funkcję y=2x+1

prosta.m

x=0:0.1:10;

y=2*x+1;

plot(x,y,'r+')

• dwóch zmiennych

mesh(x,y,z) - rysowanie prostokątnej siatki

surf(x,y,z) - rysowanie kolorowej powierzchni

x, y - wektory określające przedział zmienności argumentów funkcji

z - wektor będący rozwiązaniem funkcji

Przykład m-pliku kreślącego powierzchnię

powierzchnia.m

x=-pi:0.1:pi;

y=x;

[A,B]=meshgrid(x,y); % polecenie przygotowujące przestrzenną

% siatkę punktów x i y

z=exp(sin(A.^2+B));

surf(A,B,z)

W przypadku grafiki dwuwymiarowej Matlab umożliwia również sporządzanie wykresów dla danych dyskretnych (bar, stem, stairs) i zespolonych (compass, plot) oraz wykresów poziomicowych (contour, clabel) i histogramów (his, rose).

Podobnie jest również w przypadku grafiki trójwymiarowej. Dostępne są odmiany wymienionych już funkcji jak np. meshc, meshz, surfc , surfl , waterfall oraz szeroka gama funkcji pomocniczych, które umożliwiają uzupełnienie tworzonych wykresów niezbędnymi danymi.

Funkcje pomocnicze:

• grid on/off - powoduje włączenie/wyłączenie siatki współrzędnych

• title(`tytuł_wykresu') - tytuł wykresu

• xlabel(`opis_osi_x') ylabel(`opis_osi_y') - opisy osi wykresu

• legend(`tekst_1','text_2','tekst_3')- legenda tworzonego wykresu

• axis([x_min x_max y_min y_max])- określenie przedziału zmienności osi

6

---