Wielkości fizyczne są to takie właściwości ciał lub zjawisk które można porównać ilościowo z takimi samymi właściwościami innych ciał lub zjawisk (np.:czas, długość, kąt, prędkość, przyspieszenie). Wielkości te mogą zostać zmierzone dzięki temu możemy wyrazić je liczbowo.

Pomiar wielkości fizycznej polega na jej porównaniu z wielkością tego samego rodzaju przyjętą za jednostkę. Wielkości fizyczne umowne dzieli się na podstawowe i pochodne

Wielkości pochodne: dla których operacje definicyjne opierają się na innych wielkościach fizycznych np.: prędkość, przyspieszenie, objętość.

Wielkości podstawowe nie korzysta się z innych wielkości fizycznych. Liczba wielkości uznawanych za podstawowe jest równa minimalnej liczbie wielkości koniecznych do stworzenia zwartego i jednoznacznego opisu wszystkich wielkości fizycznych np.: czas, długość. Miarą wielkości fizycznej podstawowej jest pewna liczba jednostek. Idealny wzorzec powinien być łatwo dostępny oraz być niezmienny. Obecnie jest około 42 rzędy wielkości o około 81 rzędów wielkości rozpiętości mas.

Odległość do najbliższej gwiazdy Alta Centauri 4,3*10¹⁶ m

Promień Ziemi 6,4*10⁶ m

Grubość kartki 1*10^-4 m

Promień elektronu 1*10^-16 m

Szeroka jest również skala czasowa procesów fizycznych - wiek Ziemi ocenia się na ok. 5*10⁹ lat. Jest on przypuszczalnie o rząd wielkości mniejszy od wieku galaktyki i wieku Wszechświata.

Nowy wzorzec długości w oparciu o mierzoną w próżni długość pomarańczowej linii izotopu kryptonu Kr. Izotop ten jest pobudzony do świecenia wyładowaniami elektrycznymi. Jeden metr jest obecnie definiowany 1,6*10⁶ długości fali tej linii.

Korzyści: możliwość dokonywania dokładnych pomiarów; atomy kryptonu będące źródłem światła są identyczne, emitują światło o jednakowej długości; wybrana długość fali jest jednoznacznie związana z kryptonem, jest dokładnie określona; czysty krypton można łatwo otrzymać.

Wzorzec czasu powinien określać chwilę czasu i dać odpowiedź na pytanie jak długo zjawisko trwało lub jaka jest jego powtarzalność - częstość.

Zegar o napędzie grawitacyjnym- do jego napędzania służy sprężyna lub ciężarek. Drugim podstawowym elementem mechanizmu zegara jest urządzenie uwalniające energię sprężyny małymi porcjami w różnych odstępach czasu, podstawową jego częścią jest wahadło grawitacyjne lub sprężynowe. Dokładność pomiaru czasu może wynosić 0,05s a błąd nie przekracza 0,1s. Wykorzystane są 2 cechy wahadła niezależności okresu od amplitudy oraz stałości okresu. Innymi wzorcami są zegary kwarcowe. Wykorzystywane w nich są naturalne okresowe drgania płytki kwarcowej podtrzymywane elektrycznie. Mierzyć mogą one czas z maksymalnym błędem 0,2s/rok. W chwili obecnej za najbardziej precyzyjne uważa się zegary atomowe, w których wykorzystuje się charakterystyczne, okresowe drgania atomów cezu

Nowa definicja sekundy - sekunda jest trwaniem 9102631770 okresów promieniowania odpowiadającego przejściu pomiędzy dwoma poziomami struktury nadsubtelnej (F=4, M=0 i F=3, M=0) stanu podstawowego 2 S_1/2 atom cezu 133. Atomowy zegar pozwolił na zwiększenie dokładności pomiaru do 1/10¹¹. Obecnie może być nawet do 1/10^-15 a nawet 1/10^-18 (2005 rok)

Układ jednostek

Długość metr m

Masa kilogram kg

Czas sekunda s

Natężenie prądu amper A

Temperatura Kelwin K

Natężenie światła kandela cd

Kilogram jest masą wzorca stopu platyny z irydem. Jest ona porównywalna z 1000 cm³ czystej wody w temperaturze 4˚C

Amper-jest to natężenie prądu płynącego w dwóch nieskończenie długich równoległych przewodach (o przekroju okrągłym, znikomo małym) umieszczonych w próżni w odległości 1 m od siebie wywołując między nimi siłę 2*10^-7 N na każdy metr długości

Kelwin-jest to 1/273,6 część temperatury punktu potrójnego wody. Temperatura zera bezwzględnego T=0 K odpowiada wartości -273,15˚C

Kandela-jest to światłość, która ma w kierunku prostopadłym pole 1/6000000m² powierzchni ciała doskonale czarnego promieniującego w temperaturze krzepnięcia platyny pod ciśnieniem 101325 N/m²

Oprócz wymienionych jednostek podstawowych używa się jednostek wielokrotnych, które tworzy się na zasadzie dziesiętnego systemu podziału, dodając do jednostki podstawowej odpowiedni przedrostek. Wyjątek: jednostka czasu sekunda, minuta, godzina, doba

Tera T 10¹² centy c 10^-2

Giga G 10⁹ mili m 10^-3

Mega M 10⁶ mikro μ 10^-6

Kilo k 10³ nano n 10^-9

Hekto h 10² piko p 10^-12

Deka da 10 femto f 10^-15

Decy d 10^-1 atto a 10^-18

Układy odniesienia, układy współrzędnych.

Jeżeli położenie ciała lub układu ciał zmienia się w czasie to można powiedzieć, że ciało bądź układ są w ruchu. Inne ciało bądź układ ciał nazywa się układem odniesienia. Jeśli natomiast ciało nie zmienia swego położenia względem układu odniesienia, to pozostają one w spoczynku względem tego układu. Wybór układu odniesienia jest potrzebny do określenia ruchu lub spoczynku. Układ odniesienia powinien być wybierany tak aby był najwygodniejszy do opisu zjawisk a jednocześnie był naturalny. Ruch tramwaju najprościej jest opisywać względem przystanków bądź szyn, a nie względem gwiazd, Nie istnieje ruch ani spoczynek absolutny, jest tylko ruch i spoczynek względny. Ciało może poruszać się względem jednego układu odniesienia i być w spoczynku względem innego. Tramwaj stojący na przystanku jest względem niego w spoczynku, ale względem słońca jest w ruchu. W różnych układach odniesienia ruch może wyglądać inaczej. Ruch księżyca względem ziemi odbywa się po torze eliptycznym, ale w układzie związanym ze słońcem Księżyc porusza się po torze bardzo skomplikowanym.

Praktycznie z ciałami, które uważane są w danej chwili za układ odniesienia związany jest sztywno pewien układ współrzędnych, dzięki czemu położenie każdego punktu poruszającego się względem układu odniesienia można jednocześnie określić za pomocą trzech współrzędnych tego punktu.

W mechanice jako podstawowe stosuje się następujące układy współrzędnych

1. kartezjański- prostokątny- prawoskrętny

2. cylindryczny- walcowy

3. sferyczny- kulisty

Wybór układu powinien być odpowiedni dla określonej geometrii zjawiska. Ruch kredy rzuconej z pewnej wysokości h w dół bądź w górę w pomieszczeniu, w którym się znajdujemy, najwygodniej jest rozpatrywać posługując się układem 1) umieszczając go w jednym z naroży pomieszczenia. Położenia kredy względem tego układu w każdej chwili opisują trzy współrzędne x, y, z, jakiegoś punktu kredy.

Uproszczenie polegające na tym, że badanie ruchu całej kredy zastępowane jest badaniem ruchu jednego z jej punktów związane jest z pojęciem punktu materialnego, czyli ciała obdarzonego masą ale posiadającego rozmiary tak małe w porównaniu z rozmiarami otoczenia (pomieszczenia), tak że bez znacznego błędu można jego położenie opisać tak jak położenie punktu geometrycznego. Ruch elektronów w kondensatorze walcowym można rozpatrywać używając układu 2 a w kulistym układu 3.

Ruch punkt materialnego jest całkowicie określany, gdy podane jest równanie zmiany w czasie t współrzędnych przestrzennych q_1,q_2,q₃ (jakichkolwiek) tego punktu: q₁=q₁(t) q₂=q₂(t) q₃=q₃(t)

Równanie to jest równoważne jednemu równaniu wektorowemu r=r(t) gdzie r promień (wektor) wodzący łączący początek układu współrzędnych z poruszającym się punktem P (q_1,q_2,q₃). Gdy współrzędne prostokątne punktu P są x, y, z, (układ 1) to r=xi+ yj+ zk

i, j, k- wektory jednostkowe zgodne z dodatnimi kierunkami osi O_x, O_y, O_z.

Wektor r można nazwać wektorem przemieszczenia punktu P względem punktu O, który stanowi początek układu współrzędnych. Przemieszczenia dodają się do siebie według reguł dodawania wektorów. Jest to treść zasady niezależności ruchów. W myśl tej, jeśli ciało wykonuje równocześnie dwa lub więcej ruchów, ruchy te nie przeszkadzają sobie wzajemnie, każdy ruch odbywa się tak, jak gdyby inne ruchy nie istniały. Ilustracją tej zasady jest rsut ukośny i jego najprostsze przypadki, rzut pionowy ku dołowi i rzut pionowy ku górze oraz rzut poziomy.

Układ mechaniczny jest swobodny, jeżeli wszystkie wchodzące w jego skład punkty materialne mogą zajmować dowolne położenie w przestrzeni oraz mieć dowolną prędkość. W przeciwnym przypadku układ jest nieswobodny.

Więzy są to graniczenia nakładane na położenie lub ruch rozpatrywanego układu w przestrzeni. Jeżeli ciało może wykonywa dowolne ruchy pod wpływem wypadkowej zewnętrznych sił przyłożonych, to posiada ono trzy stopnie swobody bo do określenia jego położenia np. względem kartezjańskiego układu współrzędnych trzeba podać trzy liczby: składowe wektora i cząstki P. jeżeli może wykonywać ono ruch tylko po powierzchni, czyli jego ruch jest ograniczony (kamień na linie) to posiada ono dwa stopnie swobody, a przyczyny fizyczne ograniczające jego ruch nazywa się więzami. Równanie powierzchni lub krzywych to równanie więzów. Jeżeli powierzchnia lub krzywa więzów zmienia się w czasie podczas ruchu cząstki to więzy nazywają się reonomicznymi- niestacjonarnymi. W przeciwnym razie mamy do czynienia z więzami skleronomicznymi- stacjonarnymi.

Opory ruchu.

Wszystkie ciała poruszające się w naszym otoczeniu napotykają na pewne opory, zwane oporami ruchu. Siły oporu ośrodka są zawsze skierowane przeciwnie do wektora prędkości ciał i starają się powstrzymywać ten ruch. Opory ruchu występują zawsze wtedy, gdy badane ciała ślizgają się lub toczą po powierzchni innych ciał lub też gdy ciała poruszające się w ośrodkach takich jak gazy lub ciecze.

Przykład 1.

Na gładkiej poziomej powierzchni umieszczamy klocek, a następnie wprawiamy go w ruch. Będzie on się poruszał z malejącą prędkością, aż do chwili zatrzymania się. Odpowiedzialne za ten stan jest tarcie poślizgowe.

2. jeżeli w miejsce klocka umieścimy walec będzie działała na niego siła hamująca tarcia tocznego..

Opory ośrodka można pokazać w oparciu o kształt karoserii samochodów wyścigowych.

Opadanie ciał w cieczach, bądź w powietrzu związane jest z siłą oporu, której przyczyną jest lepkość- tarcie wewnętrzne.

Prawa tarcia- prawa Amontsa- Coulomba.

1. Siła tarcia F_t między dwoma ciałami jest proporcjonalna do siły normalnej F_n utrzymującej te ciała w zetknięciu, zwrot jej jest przeciwny do zwrotu wektora prędkości

F_t= k F_n

Siła dociskająca może być siłą ciężkości, bądź jej składowa- ruch po równi pochyłej.

2. Przy określonej sile normalnej siła tarcia poślizgowego nie zależy od powierzchni zetknięcia się ciał.

Istnieją dwa rodzaje współczynników tarcia: statyczny, kinetyczny.

Współczynnik tarcia statycznego k_s, pomnożony przez siłę normalną daje minimalną wartość siły F zwanej siłą tarcia statycznego, którą należy pokonać aby wprawić w ruch ciało spoczywające na powierzchni. Mnożąc współczynnik tarcia kinetycznego k_k rzez siłę normalną otrzymuje się współczynnik tarcia kinetycznego. Aby ciało ślizgające się po powierzchni utrzymać w ruchu .... ?

Aby poznać istote tarcia rozpatrzmy mechanizm tarcia w przypadku metali. Gładko wypolerowane powierzchnie metalu oglądane w dużym powiększeniu przypominają gładko zaorane pole z przerwami 10^-9 lub 10^-8 m. Przy zetknięciu kontakt zachodzi tylko pomiędzy szczytami wierzchołków i w tych miejscach działają siły molekularne-siły spójności. W miejscu styku występują ciśnienia powodujące powstawanie odkształceń plastycznych i tworzenie się tam trwałych połączeń-zespawane na zimno. W obszarach sąsiednich występują odkształcenia sprężyste. Jeżeli przyłoży się siłę równoległą do powierzchni metali zaczynają się ode względem siebie przesówać i następuje zerwanie połączeń, potrzebna do tego siła jest w przybliżeniu równa sile tarcia.Przy procesie zrywania połączeń międzymetalicznych podczas ślizgania następuje wyrwanie kawałeczków jednej powierzchni i przyłączanie ich do drugiej i z tym związane są procesy zużycia powierzchni metalicznych.

Metoda badania stanu zużycia-wskaźniki promieniotwórcze. Jakiekolwiek zanieczyszczenia powodują zmniejszenie się możliwości tworzenia się połączeń międzymetalicznych, a co za tym idzie zmiany siły tarcia. Bardzo dokładnie wypolerowana powierzchnia powoduje zwiększenie się powierzchni styku a zatemi rzeczywistej liczby połączeń. Wartość współczynników tarcia zwiększa się do ok. 10 lub 100 razy. Stosowanie smarów powoduje zmniejszenie siły tarcia. Opory ruchu w tym przypadku są spowodowane wyłącznie siły lepkości występujące między wartswami smaru.

Występowanie oporów ruchu w płynach związane jest z lepkością tych substancji. Pod określeniem płynów kryją się zarówno ciesze jak i gazy. Na powierzchni cieszy znajdującej się w naczyniu o głębokości d przesuwamy płaską deseczkę ze stałą prędkością V styczną do powierzchni cieczy. W tym celu do deski przykładamy siłę F styczną do powierzchni cieczy. Zgodnie z zasadą bezwładności ciecz odziałuje na deskę z siłą F₁ równą co do wartości F lecz przeciwnie skierowaną F=-F₁. Siła wypadkowa F_w=0, czyli deska porusza się ze stałą prędkością V oraz F=F₁=-η(V/d)S η- współczynnik lepkości

Warstwa cieczy przylegająca do deski porusza się z prędkością V, natomiast warstwy przyległe do dna naczynia pozostają w spoczynku. W cieczy wytwarza się gradient prędkości warstwy cieczy których głębokości różnią się o Δz mają różnicę prędkości ΔV. Zmiany owe są spowodowane oporami ruchu względem warstw wewnątrz cieczy-tarcie wewnętrzne [N*S*m^-2] lub [kg*m^-1*s^-1].

Ruch płynu pokazany na rysunku nazywa się warstwowym-laminarnym, warstewki poruszają się względem siebie z różnymi prędkościami, w zasadzie nie mieszając się. Siła F zależy, jak wynika z eksperymentów od gęstości ρ płynu, współczynnika lepkości η, prędkości ciała względem płynu V oraz od wymiarów liniowych b ciała prostopadłego do V.

R_e=V*l* ρ/ η - liczba Reynoldsa

Charakteryzuje ona przepływ płynów oraz ruch ciał w płynach. Odpowiada ona stosunkowi pracy zużytej na przyspieszenie jednostki objętości cieczy do prędkości V do pracy wykonywanej dla pokonania sił oporu lepkiego.

Prawo przepływów- gdy ruch różnych cieczy pływających z różnymi prędkościami w różnych przewodach jest opisany jednostkowymi wartościami liczby R_e, tocharakter ruchu tych cieczy jest jednakowy. Prawo to ma podstawowe znaczenie do eksperymentalnego określenia oporów ruchu. Pozwala ograniczyć przypadki przepływów laminarnych R_e<1160 lub turboelementarnych R_e>1160. Często do opisu siły oporu czołowego przy ruchu ciał w płynach stosuje się wzór Newtona:

F=C*( ρV²/2)*S

S-powierzchnia rzutu ciała na płaszczyznę prostopadłą do wektora prędkości V

C-współczynnik bezwymiarowy, zalezy od liczby R_e, jego orientacji względem płynu

Ruch w płynie ciała o kształcie kulistym

Eksperymentalnie stwierdzono, że dla bardzo małych wartości liczby R_e<<1 C=24/R_e, dla kuli S=πr² l=2r więc

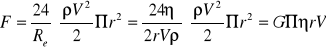
Wymiary płynu są nieograniczone. W pozostałych przypadkach wprowadza się poprawki wynikłe z ograniczonego rozmiaru naczynia. Całkowita objętość płynu płynącego laminarnie przez rurkę w odługośi l w czasie t opisuje wzór Hagena-Poisenille`a:

V-objętość

Δp-niewielka różnica ciśnień wywołujaca przepływ płynu przez cienką rurkę

Wzór ten można stosować w przypadku przepływu krwi przez elastyczne naczynia krwionośne. Warto dodać, że do przepływów laminarnych stosuje się prawo Bernouliego. W dowolnym punkcie rury suma ciśnienia zewnętrznego p hydrodynamicznego
oraz hydrostatycznego ρgh jest wielkością stałą

g - przyspieszenie grawitacyjne

Późniejsze rozważania dotyczą ośrodków ciągłych (dla ruchu w bardzo rozrzedzonych gazach pojawiają się znaczne odstepstwa)

---