Magdalena Gawrońska
nr albumu 135743
Sprawozdanie z ćwiczeń laboratoryjnych
z fizyki
Pomiar zależności oporności metali
i półprzewodników od temperatury.
Prowadzący ćwiczenia:
dr W. Kumala
Wstęp.
Przepływ prądu w metalu polega na uporządkowanym ruchu elektronów będących swobodnymi nośnikami ładunku . Zakłócenie przepływu strumienia elektronów powodujące spadek konduktywności metalu ( a tym samym wzrost rezystancji ) wywoływane jest przez dwie podstawowe przyczyny :
- w zakresie wysokich temperatur wzrasta amplituda drgań sieci krystalicznej , a tym samym przekrój czynny na rozpraszanie co powoduje osłabienie strumienia swobodnych nośników ładunku , czyli wzrost rezystancji . Dla czystych metali jednoskładnikowych zależność oporu elektrycznego od temperatury jest w przybliżeniu liniowa :
Rt=R0(1+0t)
Ro - rezystancja w temperaturze 0C ,
Rt - rezystancja w temperaturze t ,
o - temperaturowy współczynnik rezystancji w zakresie od 0 do t C :
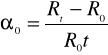
- rozpraszanie swobodnych nośników na wszelkich defektach sieciowych.
W czystych jednoskładnikowych metalach ten typ rozpraszania jest dominujący w niskich temperaturach , natomiast w temperaturze pokojowej i wyższych nie ma większego znaczenia.
Dla półprzewodników prawdziwe są powyższe spostrzeżenia o rozpraszaniu swobodnych nośników w metalach , z tym że w niskich temperaturach głównymi defektami strukturalnymi są zjonizowane atomy domieszek . Dlatego w półprzewodnikach można zauważyć silną , wykładniczą zależność konduktancji od temperatury :
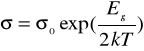
Eg - szerokość pasma wzbronionego ,
k= 1,38*10-23 JK - stała Boltzmanna ,
T - temperatura w kelvinach ,
o -stała niezależna od temperatury .
Z powyższego wzoru można bezpośrednio wyznaczyć zależność oporu od temperatury :
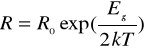
Ro - stała zależna od rodzaju i wymiarów geometrycznych półprzewodnika . Oznacza ona rezystancję jaką miałby
w nieskończenie dużej temperaturze .
W celu wyliczenia szerokości pasma zabronionego Eg należy wyznaczyć wykres zależności lnR=f(1000/T), odczytać z niego tg kąta nachylenia odcinka prostoliniowego charakterystyki i ostatnie równanie zlogarytmować stronami :
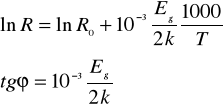
a następnie wyznaczyć Eg :
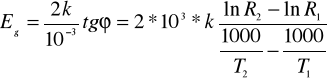
w powyższym wzorze (lnR1,1000/T1) i (lnR2,1000/T2) to współżędne punktów na początku
i końcu prostoliniowego odcinka charakterystyki ln=f(1000/T) .
Wyniki i obliczenia.
t |
Δt |
Rm1 |
Rm2 |
Rm |
Δ Rm |
[°C] |
[°C] |
[Ω] |
[Ω] |
[Ω] |
[Ω] |
16,6 |
1 |
0,105 |
0,105 |
0,105 |
0,002 |
21,6 |
1 |
0,107 |
0,107 |
0,107 |
0,002 |
26,6 |
1 |
0,109 |
0,110 |
0,110 |
0,002 |
31,6 |
1 |
0,111 |
0,112 |
0,112 |
0,002 |
36,6 |
1 |
0,113 |
0,114 |
0,114 |
0,002 |
41,6 |
1 |
0,115 |
0,116 |
0,116 |
0,002 |
46,6 |
1 |
0,117 |
0,117 |
0,117 |
0,002 |
51,6 |
1 |
0,119 |
0,119 |
0,119 |
0,002 |
56,6 |
1 |
0,121 |
0,121 |
0,121 |
0,002 |
61,6 |
1 |
0,123 |
0,123 |
0,123 |
0,002 |
66,6 |
1 |
0,125 |
0,125 |
0,125 |
0,002 |
71,6 |
1 |
0,127 |
0,127 |
0,127 |
0,002 |
76,6 |
1 |
0,129 |
0,129 |
0,129 |
0,002 |
81,6 |
1 |
0,131 |
0,131 |
0,131 |
0,002 |
86,6 |
1 |
0,133 |
0,133 |
0,133 |
0,002 |
91,6 |
1 |
0,135 |
0,135 |
0,135 |
0,002 |
Tab. 1. Pomiar rezystancji metalu w zależności od czasu.
α |
Δα |
Δα / α |
[ºC -1] |
[ºC -1] |
% |
0,0038 |
0,0001 |
2,6 |
Tab. 2. Temperaturowy współczynnik
oporności.
t |
T |
1000/T |
Rs1 |
Rs2 |
Rs |
Δ Rs |
lnRs |
[°C] |
[K] |
[K-1] |
[Ω] |
[Ω] |
[Ω] |
[Ω] |
|
16,6 |
289,6 |
3,45 |
1,192 |
0,852 |
1,022 |
0,006 |
0,022 |
21,6 |
294,6 |
3,39 |
1,067 |
0,599 |
0,833 |
0,005 |
-0,183 |
26,6 |
299,6 |
3,34 |
0,855 |
0,462 |
0,659 |
0,005 |
-0,418 |
31,6 |
304,6 |
3,28 |
0,677 |
0,379 |
0,528 |
0,004 |
-0,639 |
36,6 |
309,6 |
3,23 |
0,567 |
0,327 |
0,447 |
0,004 |
-0,805 |
41,6 |
314,6 |
3,18 |
0,491 |
0,290 |
0,391 |
0,004 |
-0,940 |
46,6 |
319,6 |
3,13 |
0,425 |
0,267 |
0,346 |
0,003 |
-1,061 |
51,6 |
324,6 |
3,08 |
0,363 |
0,243 |
0,303 |
0,003 |
-1,194 |
56,6 |
329,6 |
3,03 |
0,312 |
0,201 |
0,257 |
0,003 |
-1,361 |
61,6 |
334,6 |
2,10 |
0,265 |
0,171 |
0,218 |
0,003 |
-1,523 |
66,6 |
339,6 |
2,94 |
0,223 |
0,147 |
0,185 |
0,003 |
-1,687 |
71,6 |
344,6 |
2,90 |
0,193 |
0,128 |
0,161 |
0,003 |
-1,829 |
76,6 |
349,6 |
2,86 |
0,163 |
0,115 |
0,139 |
0,003 |
-1,973 |
81,6 |
354,6 |
2,82 |
0,136 |
0,105 |
0,121 |
0,002 |
-2,116 |
86,6 |
359,6 |
2,78 |
0,111 |
0,100 |
0,106 |
0,002 |
-2,249 |
91,6 |
364,6 |
2,74 |
0,097 |
0,097 |
0,097 |
0,002 |
-2,333 |
Tab. 3. Pomiar rezystancji półprzewodnika w zależności od czasu
Eg |
Δ Eg |
Δ Eg/ Eg |
||
[J] |
[eV] |
[J] |
[eV] |
% |
9,07ּ10-20 |
0,57 |
0,11 ּ10-20 |
0,01 |
2 |
Tab. 4. Szerokość przerwy energetycznej w półprzewodniku.
Obliczenia:
Temperaturowy współczynnik
oporności.
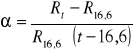
Rt -rezystancja metalu w temp. końcowej
R16,6 -rezystancja metalu w temp. pokojowej
Rt=A⋅t + B
R16,6=A⋅16,6 + B
A = 0,0004 ± 4,35⋅10-6 [Ω/°C]
B = 0,0991 ± 0,0003 [Ω]
(Odczytano z regresji liniowej.)
![]()
![]()
![]()
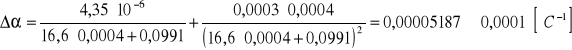
Szerokość przerwy energetycznej
w półprzewodniku.
![]()
(A= 3,2856 ± 0,0383 - odczytano z regresji liniowej)
![]()
![]()
α = 0,0038 ± 0,0001 [ºC -1] Eg = 9,07ּ10-20 ± 0,11 ּ10-20 [J] Eg = 0,57 ± 0,01 [eV] |
Wnioski.
Błędy którymi obarczone są wyniki otrzymane w ćwiczeniu zostały spowodowane przez dwie zasadnicze przyczyny :
- odczyt temperatury na skali termometru przy szybkich zmianach jej wartości był jedynie przybliżony co spowodowało niewielkie rozbieżności wyników (dla tej samej temperatury) otrzymanych przy ogrzewaniu i chłodzeniu rezystorów ,
- niedokładność multimetrów używanych do pomiaru rezystancji , która dała błąd dochodzący do 2% wartości mierzonej .
Zależności określone w ćwiczeniu (zarówno lnRt=f(1000/T) , jak i Rm=f(t)) mają postać linii prostych, zgodnie z wytycznymi teoretycznymi na ten temat. Eksperyment potwierdza w granicach błędu liniowy związek miedzy temperaturą metalu a jego rezystancją. Wykonane ćwiczenie dowodzi, ze wraz ze wzrostem temperatury półprzewodnika rośnie liczba elektronów w pasmie przewodnictwa, a tym samym maleje jego rezystancja. Również wartości temperaturowego współczynnika rezystancji = 0,0038 [1/°C] i szerokość pasma wzbronionego dla półprzewodnika Eg = 0,57eV pokrywają się z wartościami podawanymi w tablicach .
Zjawisko zmiany wartości rezystancji pod wpływem zmian temperatury znalazło szerokie zastosowanie w technice. Często stosowane są termometry oporowe platynowe pozwalające mierzyć temperatury w zakresie od -200 do +550C . Pomiar tą metodą może być bardzo dokładny po zastosowaniu odpowiednio wysokiej klasy miernika rezystancji wyskalowanego w jednostkach temperatury .
Zestawienie wyników:
α = 0,0038 ± 0,0001 [ºC -1]
Eg = 9,07ּ10-20 ± 0,11 ּ10-20 [J]
Eg = 0,57 ± 0,01 [eV]
Wyszukiwarka