Rok akademicki 2009/2010

Sprawozdanie

ćw. nr 4

Temat:

Pomiar lepkości cieczy metodą Stokesa

Wykonał:

Piotr Maślanka L 5

I. Wstęp teoretyczny:

Cieczą doskonałą nazywamy ciecz nieściśliwą i nielepką. Ciecz nieściśliwa to ciecz, która nie zmienia swojej objętości pod wpływem zmian ciśnienia. Ewentualna zmiana objętości, np. cieczy zamkniętej w strzykawce pod wpływem siły działającej na tłoczek wiąże się z wykonaniem pracy po przesunięciu odpowiadającemu zmianie objętości, a więc z dostarczeniem (odebraniem) pewnej energii cieczy. Zatem u cieczy doskonałej nie jest zużywana energia na zmianę objętości i jeżeli pominie się zmiany temperatury cieczy, to można stosować do niej zasadę zachowania energii mechanicznej. Z zasady tej można wyprowadzić równanie Bernouilliego:

gdzie:
- ciśnienie w strudze poruszającej się cieczy,

h - wysokość wzniesienia w danym miejscu strugi,

v - prędkość cieczy w danym miejscu,

- gęstość cieczy.

Pierwsze dwa człony możemy ująć ogólną nazwą: ciśnienie statyczne Ps = p + ρgh, natomiast trzeci człon to ciśnienie dynamiczne Pd = ½ρv2.

Ps jest to ciśnienie wywierane prostopadle do kierunku przepływu, a Pd - równolegle.

Skoro ich suma stanowi konstans, to należy przypuszczać, że w obszarach większej prędkości przepływu, ciśnienie statyczne będzie mniejsze.

Przejdźmy teraz do praktycznych przykładów. Mamy balię wypełnioną wodą, z otworem u dołu, przez który ta woda wypływa. Z jaką prędkością vwyp będzie ów wypływ przebiegał?

Załóżmy, że przy powierzchni (punkt 1) woda nie porusza się w ogóle. A więc ma tylko ciśnienie statyczne równe: p + ρgh1. Tuż u wylotu (w punkcie 2) ciecz ma ciśnienie statyczne równe: p + ρgh2 i ciśnienie dynamiczne: ½ρvwyp2.

Możemy, zgodnie z prawem Bernoulliego, utworzyć równanie:

p + ρgh1 = p + ρgh² + ½ρvwyp²

zatem: ρgh1 - ρgh² = ½ρvwyp²

gh1 - gh² = ½vwyp²

Widzimy, że prędkość wypływu rośnie dla większych wysokości słupa cieczy w balii. Wzór ten jest identyczny z tym, który zastosowalibyśmy dla spadku cieczy z wysokości (h1 - h2).

Zjawisko spadku ciśnienia statycznego kosztem wzrostu ciśnienia dynamicznego (i odwrotnie) można łatwo zaobserwować przy pomocy rurki, której przekrój nie jest na całej długości jednakowy (ma ona przewężenia), a do pomiaru ciśnienia statycznego służą rurki, ustawione prostopadle do kierunku przepływu cieczy.

Podczas przypływu w rurce, ciecz ma w miejscu przewężenia większą prędkość. Jest tak dlatego, że w jednostce czasu przez każdą powierzchnię przekroju rurki musi przejść ta sama ilość cieczy. Przy mniejszym przekroju musi odbywać się to na większej długości. Jest to możliwe tylko wtedy, gdy ciecz porusza się szybciej.

Ten efekt jest wyraźnie widoczny w strzykawkach. Posuwamy tłok wolno, a ciecz wypływa z przewężenia strzykawki ze znacznie większą prędkością.

Wracając do naszej rurki: zauważymy, że poziom cieczy w rurce prostopadłej do przewężenia (będący miernikiem ciśnienia statycznego), jest wyraźnie niższy niż na odcinku o normalnym przekroju.

A więc tam gdzie rośnie ciśnienie dynamiczne (ze wzrostem prędkości), tam spada składowa statyczna.

Jeszcze jeden przykład z życia wzięty. Jeśli przytkniemy 2 kartki papieru do obydwóch policzków i dmuchniemy pomiędzy nie, to paradoksalnie zaczną one do siebie przylegać. Wytłumaczenie tego zjawiska jest proste. Strumień wydmuchiwanego powietrza ma ciśnienie dynamiczne, a więc ciśnienie statyczne (działające w bok - na kartki) będzie mniejsze od tego, które działa na kartki z zewnątrz (od statycznego powietrza). Zatem ciśnienie zewnętrzne przeważy i dlatego kartki przylgną do siebie.

II. Metodologia wykonania pomiarów

1. Zmierzyliśmy długość drogi l, którą będą przebywać kulki z dokładnością ±1mm.

2. Wybraliśmy 10 jednakowych kulek, wyznaczyć ich średnicę d₁, mikromierzem z dokładnością ±0.01mm.

3. Zmierzyliśmy czas t₁ spadania kulek stoperem z dokładnością ±0.5s

4. Pomiary z pkt. 2 i 3 powtórzyć dla dziesięciu kulek wykonanych z tego samego materiału o innej średnicy d₂.

5. Zmierzyliśmy średnicę wewnętrzną rury wiskozymetru i wyniosła ona R=4,5cm.

6. Uzyskane wyniki pomiarów zestawiliśmy w tabeli pomiarów.

III. Obliczenia

1. Obliczyliśmy wartość n dla każdej pary danych eksperymentalnych korzystając ze wzoru:

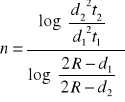
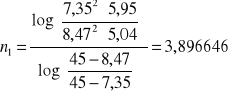
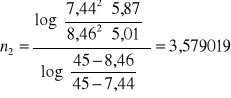
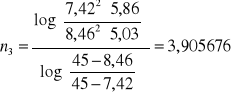
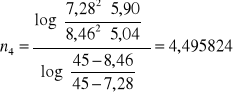
Wyznaczyliśmy wartość średnią
:

Obliczyliśmy niepewność standardową
na podstawie wzoru:

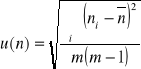
gdzie m jest liczbą wykonanych pomiarów

2. Dla wielkości t i d wyliczyliśmy niepewności standardowe u(t) i u(d):

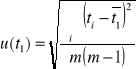
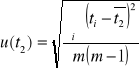
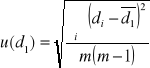
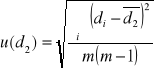
3. Obliczyliśmy niepewność standardową u(l):

4. Wyliczyć wartość współczynnika lepkości gliceryny η.

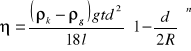
gdzie:
-gęstość kulki

-gęstość gliceryny
,g -przyspieszenie ziemskie
,

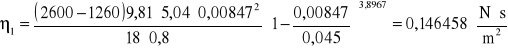
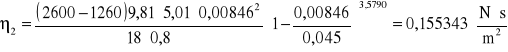
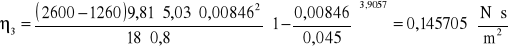
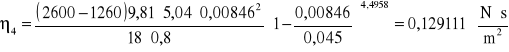
5. Obliczyć niepewność standardową u(η) metodą przenoszenia niepewności.

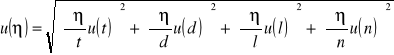
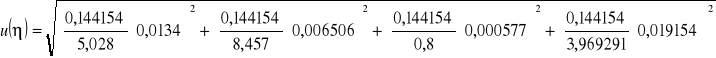
IV. Wnioski

Wartość tablicowa współczynnika lepkości gliceryny w temperaturze
wynosi 0,945
. Wyznaczona przez nas wartość współczynnika lepkości gliceryny wyniosła
. Różni się ona od wartości tablicowej. Przyczyną wystąpienia tak wielkiej rozbieżności może być zawartość wody w glicerynie wypełniającej wiskozymetr, która powoduje duży spadek współczynnika lepkości. Również powodem rozbieżności wyniku z wartością tablicową może być temperatura, w której dokonywano doświadczenia, a która nie brana była pod uwagę.

---