Ekonometria zajmuje się ustaleniem i szacowaniem na podstawie danych statystycznych, ilościowych zależności zachodzących w sferze zjawisk gospodarczych.

Model ekonometryczny to funkcja Y zmiennych objaśniających X o postaci analitycznej funkcji Y = f (X,b), której parametry „b” wyznaczono z dokładnością liczbową na podstawie materiałów statystycznych opisującego kształtowanie się zmiennej objaśnianej i zmiennych objaśniających.

Etapy budowy modelu ekonometrycznego:

1. ustalenie zmiennej objaśnianej

2. ustalenie listy zmiennych objaśniających

3. ustalenie postaci analitycznej modelu

4. zebranie materiału statystycznego o zmiennych objaśnianej i objaśniających

5. wyznaczenie parametrów

6. weryfikacja modelu

7. wykorzystanie modelu

Ustalenie listy zmiennych objaśniających.

Powinny być silnie skorelowane ze zmienną objaśnianą, a słabo ze sobą.

Ustalenie postaci analitycznej modelu:

Odwołujemy się do: wskazań teorii, intuicji, współczynników innych badań, własności funkcji matematycznych, testów statystycznych.

Weryfikacja modelu:

1. merytoryczna (zdrowy rozsądek)

2. statystyczna

Wykorzystanie modelu:

• prognozowanie - wypowiedź o wartości zjawiska w ustalonym momencie czasu w przyszłości

• symulacja i scenariusze

• syntetyczny opis zależności zmiennych zmiennej objaśnianej od zmiennej objaśniającej

Klasyfikacja modeli ekonometrycznych:

1. ze względu na liczbę zmiennych objaśniających:

• z jedną zm. objaśniającą;

• z wieloma zm. objaśniającymi

1. ze względu na postać analityczną:

• liniowe;

• nieliniowe (wykładnicze, potęgowe)

1. ze względu na liczbę zm. objaśnianych:

• z jedną zm. objaśnianą - jednorównianiowe;

• modele dla układu zm. objaśnianych (wielorównianiowe)

1. ze względu na interpretację zm. objaśniających:

• modele o interpretacji parametryczno-skutkowej, w których wszystkie zm. objaśniające są przyczynami kształtowania się zm. objaśnianej

• modele sympatomatyczne, w których występują zmienne będące symptomami zjawiska, będących przyczynami zmiennej objaśnianej

• trendy - jedyną zmienną objaśniającą jest zmienna czasowa

Modele klasyczne - gdy powiązanie między zm. objaśnianą a zm. objaśniającymi jest stabilne czyli takie samo co do postaci analitycznej zm. objaśniających - wartości parametrów

Model jest segmentowy gdy w zbiorze wyników obserwacji pojawiają się niepuste i rozłączne podzbiory takie, że:

• dla danego podzbioru powiązanie jest klasyczne

• przynajmniej dwa podzbiory różnią się albo postacią analityczną albo (i) zestawieniem zmiennych objaśniających albo (i) wartościami parametrów

Model lokalny - powiązanie zm. objaśnianej ze zm. objaśniającymi jest różne ze względu na postać analityczną, listę zm. objaśniających, wartości parametrów.

Klasyczna metoda MNK polega na takim wyznaczeniu parametrów modelu aby SKR między zaobserwowanymi wartościami zmiennej objaśnianej, a odpowiednimi wartościami teoretycznymi (niemodelowanymi) były jak najmniejsze




y - empiryczne, y' - teoretyczne

MNK dla modelu z jedną zm. objaśniającą




Wsp. kierunkowy




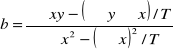
Wyraz wolny




T - numery obserwacji

Obliczanie MNK

1. zrobić tabelę CROSS - zawiera sumy iloczynów wartości wszystkich par zmiennych występujących w modelu:

	Y	X	1
Y
X
1
	X^TY	X^TX

2. obliczyć




np.


3. obliczyć




4. podstawić do wzoru




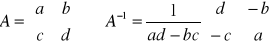
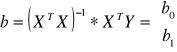
Weryfikacja modelu

• weryfikacja merytoryczna (czy model jest zgodny z teorią ekonometrii). Badamy znaki i skalę parametrów, czy model można ekstrapolować

Dopasowanie modelu - badany przy pomocy współczynnika determinacji

Współczynnik rozbieżności - mierzy tę część zaobserwowanej zmienności zm. objaśnianej, która nie została przez model wyjaśniona




SKR - suma kwadratów reszt

OSK - ogólna suma kwadratów

wr jest najmniejsze, ale powinno być<0,1 (czyli mniejsze niż 10%)







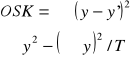
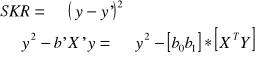
Współczynnik determinacji (zgodności) wskazuje jaka część ogólnej zaobserwowanej zmienności zm. objaśnianej została wyjaśniona przez model ekonometryczny

R²=1-wr (jeśli wr≤1)

Współczynnik determinacji ma wartość z przedziału <0,1> i powinien być większy od 0,9 (90%)

Obliczanie:

1. OSK

2. SKR

3. wr

4. R²=1-wr

Istotność zm. objaśniających

Wszystkie zm. objaśniające modelu ekonometrycznego muszą być istotne (a są istotne gdy parametr przy nich stojący jest istotnie różny od zera).

Obliczanie istotności zam. objaśniających

1. obliczamy empiryczną t_k statystyką Studenta dla badanej zm. objaśniającej:




b_k - parametr stojący przy zmiennej

d_k - szacunkowy błąd średni




c_k - to k-ty element przekątniowy macierzy odwrotnej (X^TX)^-1




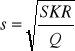
s - odchylenie standardowe składników

Q - liczba stopni swobody

Q = T - K

T - liczba obserwacji

K - liczba szacowanych parametrów

2. ustalamy krytyczną wartość statystyki Studenta t_kR (z tablic)

3. jeżeli │t_k│>t_kR moduł empirycznej statystyki Studenta jest większy od wartości krytycznej to zmienną objaśniającą uznajemy za istotną.

Przykład:

Empiryczna statystyka Studenta dla dochodu wynosi 3 i jest większa od wartości krytycznej. Dochód jest więc istotną zmienną objaśniającą.

Gdy któraś zmienna jest nieistotna to trzeba ją wykluczyć z modelu i powtórnie oszacować model - zapewne zmienią się wartości parametrów.

Linearyzacja funkcji

Nazwa funkcji	Wzór funkcji	Model
Liniowy
Potęgowa
Wykładnicza
Typu S
Hiperbola
Podwójna hiperbola
Pierwiastkowa
logarytmiczna

Praca pochodzi z serwisu www.e-sciagi.pl

---