POLITECHNIKA ŚLĄSKA

W GLIWICACH

MECHANIKA I BUDOWA MASZYN

KRYSTALICZNA STRUKTURA METALI

Semestr I

Grupa 4

Łukasz Wychrystenko

1. Krystaliczna struktura metali

Prosta sieciowa - jest ot każda prosta łącząca środki dowolnych dwóch atomów w krysztale.

Parametr sieci - jest to najbliższa odległość otworów na prostej sieciowej w sieci przeciwłącznej.

Płaszczyzna sieciowa - przesunięcie, tzw. Translacja prostej sieciowej, o period identyczności (parametr sieci) w kierunku wzdłużnym od kierunku prostej powoduje znalezienie płaszczyzny sieciowej.

Sieć przestrzenna - płaszczyzna sieciowa poddana translacjom w kierunku do niej nierównoległym tworzy sieć przestrzenną.

Trzy rodziny równoległych płaszczyzn sieciowych dzielą sieć przestrzenną na identyczne równoległościany o parametrach a, b i c stanowiących podstawowe periody identyczności (parametry) sieci. Równoległościany te są nazywane elementarnymi komórkami sieciowymi i w pełni charakteryzują dany kryształ o sieci prymitywnej. Struktura sieciowa może być opisana przez jej podstawowe periody identyczności (parametry sieci) a, b i c oraz były między nimi zawarte

, , γ

Proste elementy sieci - jakie mogą występować w kryształach to środek, osie i płaszczyzny symetrii.

Gęstość wypełnienia sieci rdzeniami otoczeniowymi charakteryzuje liczba koordynacyjna L_k , równa liczbie najbliższych i równa oddalonych rdzeni otoczeniowych w sieci krystalicznej.

W zależności od tego, czy elementy komórki sieciowej mają otwory wyłącznie na narożach (komórki prymitywne), czy także wewnątrz lub na ścianach bocznych (komórki złożone), w ramach układów krystalicznych występujących łącznie 14 typów sieci przestrzennej Bravais'go:

1. trójskośna prymitywna.

2. jednoskośna prymitywna.

3. jednoskośne centrowana na podstawach.

4. rombowa prymitywna.

5. rombowa centralowa na podstawach.

6. rombowa przestrzennie centralizowana.

7. rombowa ścienne centralizowana.

8. heksagonalna.

9. romboedyczna.

10. typowalna prymitywna.

11. typowalna przestrzennie centrowana.

12. tegularna prymitywna.

13. tegularna przestrzennie centralizowana.

14. tegularna ściennie centralizowana.

1. Określanie węzłów, kierunków i płaszczyzn w sieci krystalograficznej dla każdego elementu sieci dokonuje się tego przez podanie trzech liczb:

• współrzędne węzła sieciowego - określają liczby periodów identyczności a, b i c, o które jest oddalony węzeł od początku układu współrzędnych odpowiednio wzdłuż jego osi x, y, z. Pozycje otoczów centrujących podstawy, ściany lub przestrzeń złożonej opisuje się „współrzędnymi ułamkowymi”.

• Współczynnik kierunków - są to kierunki sieciowe. Kierunek krystolograficzny opisuje współrzędne węzła najbliższego od początku układu, przez który przechodzi prosta równoległa do analizowanego kierunku, przesunięta do początku układu.

• Wskaźnik płaszczyzn - w celu oznaczenia płaszczyzny sieciowej należy określić liczby periodów identyczności, odciętych przez daną płaszczyznę na

Poszczególnych osiach układu współrzędnych x, y, z, wyznaczyć ich odwrotność i następnie otrzymane ułamki sprowadzić do wspólnego mianownika. Liczniki ułamków o wspólnym mianowniku oznaczamy h, k, l stanowią wskaźniki sieciowe płaszczyzny.

Większość metali krystalicznych w układach krystalograficznych charakteryzuje się symetrią i dużą gęstością zapełnienia sieci przestrzennej otaczanymi, w szczególności w sieciach:

• A1ściennie centralizowanej układu regulowanego (RSC).

Elementarną kostkę A1 w kształcie sześcianu tworzy 14 rdzeni atomowych. Spośród nich 8 rdzeni atomowych jest usytuowana w narożach, natomiast sześć w środku geometrycznym ścian bocznych sześcianu. Sieć tu należy do najczęściej wypełnionych rdzeniami otoczeniowymi liczba koordynacyjna wynosi Lk=12.

• A2 przestrzennie centrowanej układu regulacyjnego (RPC) w tej komórce elementarnej znajduje się 9 rdzeni atomowych, w tym 8 na narożach sześcianu, jeden zaś w jego środku geometrycznym. Liczba koordynacyjna wynosi 2x=8. Sieć A2 charakteryzuje się mniejszą gęstością wypełnienia rdzeniami atomowymi od sieci A1(siec A1=4, sieć A2=2).

• A3 heksagonalnej o gęstym ułożeniu atomów (HGU). W sieci A3 o gęstym złożeniu rdzeni otoczeniowych z trzema elementami komórki sieciowej są złożone z 17 rdzeni atomowych, z których 12 znajduje się w narożach prostopadłościanu o podstawie sześciokąta foremnego, dwa w środku geometrycznym podstaw, a trzy pozostałe są symetrycznymi we wnętrzu elementarnej komórki sieciowej.

a) b) c)

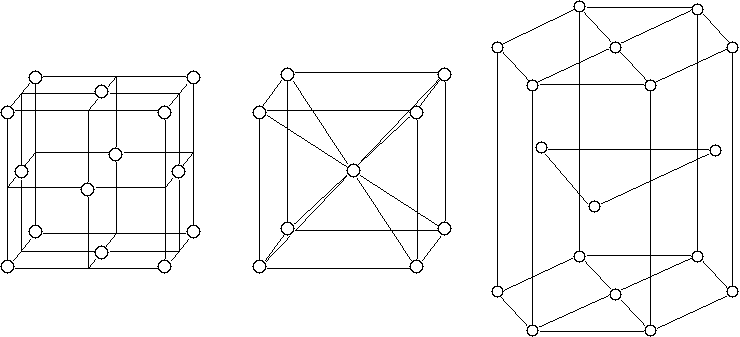
Rys. a) sieć A1; b) sieć A2; c) sieć A3

2. Wady budowy krystalicznej

1. Wady punktowe budowy krystalicznej

Do wad punktowych, cechujących się niewielkimi wymiarami we wszystkich kierunkach, należą wakanse, tj. wolne węzły w sieci krystalicznej oraz atomy międzywęzłowe, które zajęły pozycje w lukach, opuszczając węzły sieci na skutek drgań cieplnych. Obecność zarówno wakansów, jak i atomów międzywęzłowych, powoduje wokół niej lokalne odkształcenia sieci przestrzennej kryształu, zwane odpowiednia kontrakcją lub ekspansją.

2. Mechanizm tworzenia wad punktowych

Liczba wad punktowych budowy krystalicznej jest funkcją temperatury. Podwyższeniu temperatury towarzyszy wzrost amplitudy drgań cieplnych, co ułatwia opuszczenie przez rdzenie atomowe pozycji w węźle sieci krystalicznej: są to tzw. procesy aktywowane cieplnie. Wyróżnia się:

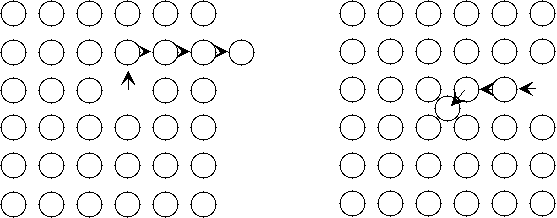
1. Defekt Schottliy'go - polega na przemieszczaniu się atomu w miejsce sąsiadującego, w wyniku czego powstaje wakans w innym miejscu sieci.

2. Defekt Frekla - związany jest z jednoczesnym utworzeniem wakansu i atomu międzywęzłowego i jest nazywany defektem Frukla i polega na przeniesieniu się rdzeniu atomowego w pozycji węzłowej do przestrzeni międzywęzłowej.

Zjawisko przemieszczania się atomów we własnej sieci krystalicznej jest nazywane samodyfuzją.

rys a) Schottky'ego rys b) Frekla

3. Dyslokacje

Nieliniowymi wadami budowy krystalicznej są dyslokacje

• krawędziowe.

• śrubowe.

• mieszane.

Dyslokacja krawędziowa - jest to półpłaszczyzna sieciowa umieszczona między nieco rozsuniętymi płaszczyznami sieciowymi kryształu o budowie promieniowej. W zależności od położenia dodatkowej półpłaszczyzny dyslokacje mogą być dodatnie, oznaczone , lub ujemnie o oznaczeniu T.

Dyslokacja śrubowa to defekt liniowy struktury krystalicznej spowodowany przemieszczeniem części kryształu wokół osi, zwanej linią dyslokacji śrubowej. Dyslokacje śrubowe mogą być prawoskrętne lub lewoskrętne.

Dyslokacje mieszane są to dyslokacje o dowolnie orientacji wektora Burgersa względem linii dyslokacji, można je traktować jako złożone na siebie dyslokacje krawędziowe i śrubowe. Dyslokacje tworzą w obrębie kryształu zamknięte pętle, które nie mogą być przerwane, chyba że dyslokacjami zmieszamy, natomiast odcinki pętli, do których wektor Burgersa jest prostopadły lub równoległy, są odpowiednio dyslokacjami krawędziowymi lub śrubowymi.

4. Wektor Burgersa - charakteryzuje wielkość dyslokacji i wywołane nią odchylenie. Wektor ten wyznacza się tworząc tzw. woutur Burgersa jego nie zamknięta część będzie taka sama i równa wektorowi Burgersa. Dyslokacja krawędziowa ma wektor Burgersa prostopadły do swej linii.

5. Wspinanie dyslokacji

Dyslokacje krawędziowe przemieszają się również przez wspinanie, które podzielić można na:

• wspinanie dodatnie, które polega na odłączeniu się atomów od krawędzi płaszczyzny i przemieszczeniu się ich droga dyfuzji do wakansów.

• Wspinanie ujemne(proces odwrotny) polega na przełączeniu się dyfundujących atomów do płaszczyzny.

Procesy te są związane z dyfuzyjnym transportem masy i dlatego proces ten wymaga podwyższenia temperatury.

6. Gęstość dyslokacji - dyslokacje powstają zarówno podczas krystalizacji metali, jaki i w stanie stałym. Całkowita długość linii dyslokacji przypadającą na jednostkę objętości kryształu nazywa się gęstością dyslokacji.

7. Oddziaływanie między dyslokacjami

Dyslokacje przemieszczające się w płaszczyźnie poślizgu, stykają się, wzajemnie na siebie oddziaływują. Dwie jednoimieniowe dyslokacje przemieszają się w tej samej płaszczyźnie poślizgu odpychają się wzajemnie (podobnie śrubowe). Dwie dyslokacje o przeciwnie skierowanych wektorach Burgersa - zarówno krawędziowe, jak i śrubowe - przyciągają się w wyniku tego następuje zlikwidowanie obydwu dyslokacji reagujących ze sobą, a zjawisko to nazywa się anihilacją dyslokacji różnoimiennych.

Dyslokacje przemieszczające się w nierównoległych płaszczyznach poślizgu przemieszczają się wzajemnie tworząc w każdej z płaszczyzn uskok.

1

2

---