LABORATORIUM FIZYKI
Ćwiczenie 37
„Dyfrakcja elektronów i światła na sieci krystalicznej”
Wydział Mechatroniki
Jakub Krzywiec;
grupa 26; zespół 7
Wstęp
Celem ćwiczenia było zbadanie naturalnej aktywności optycznej roztworu cukru w wodzie destylowanej a także obliczenie skręcenia właściwego roztworu ze wzoru:
![]()
gdzie: α - kąt skręcenia płaszczyzny polaryzacji światła, γ - skręcenie właściwe roztworu,
h - grubość warstwy roztworu, c - stężenie roztworu
W drugiej części ćwiczenia badaliśmy zjawisko Faradaya i wyznaczaliśmy stałą Verdeta z
zależności:
![]()
gdzie: α - kąt skręcenia płaszczyzny polaryzacji światła, V - stała Verdeta, h - grubość warstwy optycznie aktywnej, B - wartość wektora indukcji magnetycznej pola w którym znajduje się warstwa optycznie aktywna
Układ pomiarowy:
Układem pomiarowym w tym ćwiczeniu był polarymetr półcieniowy:
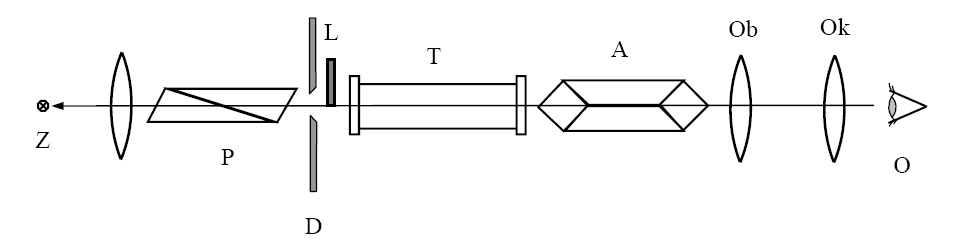
Objaśnienia do rysunku: Z- lampa sodowa, P - polaryzator, D - kolisty otwór w przesłonie, L - płytka kwarcowa Laurenta, T - rurka wypełniona badanym roztworem, A - analizator, Ob - obiektyw, Ok - okular, O- obserwator
Układ pomiarowy opiera się na zjawisku bardzo dużej czułości ludzkiego oka na różnice jasności dwóch znajdujących się obok siebie obszarów. Światło z lampy sodowej Z przechodzi przez polaryzator P i pada na kolisty otwór w przesłonie D którego połowa jest zasłonięta płytką kwarcową Laurenta zwanej również półfalówką, światło przy jej pomocy jest rozdzielone na dwa pola o różnym stopniu jasności. Gdy obrócimy analizator o kąt jaki skręca płaszczyznę roztwór aktywny optycznie, pola stają się jednakowo jasne a my możemy odczytać kąt skręcenia płaszczyzny.
W drugiej części ćwiczenia układ wygląda bardzo podobnie tylko zamiast T- rurki wypełnionej badanym roztworem, jest pręt szklany otoczony solonoidem podłączonym do zasilacza, dzięki przepuszczeniu prądu przez solonoid otrzymujemy pole magnetyczne w którym pręt szklany staje się aktywny optycznie, jest to wymuszona aktywność optyczna.
Przebieg ćwiczenia, wyniki i ich opracowanie:
W polarymetrze umieściliśmy w polarymetrze kuwetę napełnioną wodą destylowaną a następnie obracając analizatorem znajdujemy położenie gdy wszystkie pola są jednakowo jasne i odczytujemy zerowy kąt skręcenia płaszczyzny polaryzacji, dla prawego noniusza : 0°, dla lewego -0,1° który potem będziemy odejmować od każdego pomiaru dla lewego noniusza. Następnie w polarymetrze umieściliśmy kuwetę z wodą destylowaną z roztworem 1g, 2g, 4g, 6g, 8g, 10g i nieznanej ilości cukru. Następnie ustalaliśmy skręcenie płaszczyzny polaryzacji i spisywaliśmy wyniki
Masa cukru [g] |
Stężenie roztworu [%] |
Kąt skręcenia prawy noniusz |
Kąt skręcenia lewy noniusz |
Kąt skręcenia [rad] |
1 |
2% |
1.2 |
1.25 |
0,01963 |
2 |
4% |
3.9 |
3.9 |
0,06629 |
4 |
8% |
7.45 |
7.45 |
0,12822 |
6 |
12% |
11.25 |
11.35 |
0,19538 |
8 |
14% |
14.6 |
14.8 |
0,25469 |
10 |
20% |
17.75 |
17.7 |
0,30746 |
X |
X |
21 |
21.05 |
0.36679 |
Wyniki w tabeli po uwzględnieniu odczytania z noniusza skręcenia zerowej płaszczyzny polaryzacji, kąt skręcenia obliczyliśmy licząc średnią arytmetyczną z pomiarów z lewego i prawego noniusza ponieważ uznaliśmy że oba pomiary są jednakowo ważne ponieważ oba noniusze powinny działać tak samo więc ich waga uwzględniona w średniej jest jednakowa, średnia arytmetyczna będzie więc najlepszym przybliżeniem kąta skręcenia.
Na podstawie danych z tabelki wykonujemy wykres kąta skręcenia od stężenia roztworu w programie ORIGIN a następnie linearyzujemy zależność metodą sumy najmniejszych kwadratów. (WYKRES 1)
Obliczenie współczynnika skręcenia właściwego roztworu γ:
Z zależności :![]()
wynika iż współczynnikiem liniowości jest ![]()
które odpowiada parametrowi B na wykresie.
B=1,58565 ±0,05117, h jest to długość kuwety i wynosi h=149±1 mm
![]()
Ponieważ wykonywaliśmy tylko 6 pomiarów to błąd przypadkowy należy pomnożyć przez współczynnik t-Studenta dla 6 pomiarów i 2 stopni swobody, wynosi on 1,29 a więc:
ΔB= 0,05117*1,29=0,06601
natomiast błąd pomiaru kuwety wynika z niedokładności przyrządu pomiarowego jakim była linijka i wynosi Δh=1 mm
Błąd całkowity policzenia parametru ![]()
obliczamy przy pomocy różniczki zupełnej:
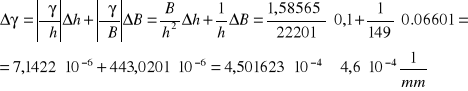
Ostatecznie:
![]()
Obliczenie stężenia C roztworu o nieznanej zawartości cukru:
Dzięki obliczeniu parametru ![]()
czyli skręcenia właściwego dla roztworu cukru z wodą, zmierzeniu długość kuwety i skręcenia polaryzatora roztworu o nieznanej zawartości cukru możemy obliczyć jego stężenie:

Błąd obliczenia stężenia roztworu o nieznanej zawartości cukru
Błąd Δα jest to błąd systematyczny pochodzący z odczytu kąta z noniusza i wynosi 0.05°
![]()
Błąd całkowity obliczania stężenia liczymy metodą różniczki zupełnej:
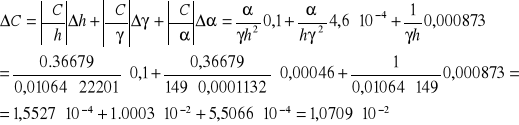
Ostatecznie C nieznanego roztworu:![]()
Wyznaczenie różnicy współczynników załamania fali spolaryzowanej prawo i lewo-skrętnie
Różnicę ![]()
wyznaczamy na podstawie zależności ![]()
gdzie: k- stała falowa a h- długość kuwety.
Obliczenie stałej falowej k dla lampy sodowej (λ=589,3nm):
![]()
mając stała k możemy obliczyć ![]()
z zależności:
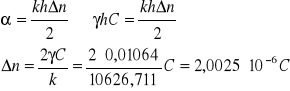
Zjawisko Faradaya
Wyliczamy zależność indukcji magnetycznej B z zależności ![]()
gdzie ![]()
natężenie prądu I [A] |
wartość indkucji magnetycznej B [Tesla] |
skręcenie zmierzone a[°] |
kąt skręcenia płaszczyzny polaryzacji a [°]
|
kąt skręcenia płaszczyzny polaryzacji a [rad]
|
|
|
|
|
|
0 |
0 |
98,95 |
|
|
0,5 |
0,00812587 |
102,3 |
3,35 |
0,05843889 |
1 |
0,01625174 |
103,5 |
4,55 |
0,07937222 |
1,5 |
0,02437761 |
104,8 |
5,85 |
0,10205 |
2 |
0,03250349 |
105,65 |
6,7 |
0,11687778 |
2,5 |
0,04062936 |
106,83 |
7,88 |
0,13746222 |
3 |
0,04875523 |
108,15 |
9,2 |
0,16048889 |
3,5 |
0,0568811 |
108,75 |
9,8 |
0,17095556 |
4 |
0,06500697 |
110,3 |
11,35 |
0,19799444 |
4,5 |
0,07313284 |
111,48 |
12,53 |
0,21857889 |
5 |
0,08125871 |
112,4 |
13,45 |
0,23462778 |
Wartości liczby zwojów, długości solenoidu, i długości pręta spisaliśmy z etykietki na solenoidzie: liczba zwojów N =4330, długość solenoidu L[mm]=280, długość pręta H[mm]=156
Za pomocą programu ORIGIN rysujemy wykres zależności kąta kąta α od natężenia prądu płynącego przez solenoid I[A] WYKRES 2
Rysujemy wykres α od B, za pomocą programu origin, z zależności:
![]()
widać że współczynnikiem kierunkowym prostej jest iloczyn ![]()
WYKRES 3
Wyliczamy stałą Verdeta
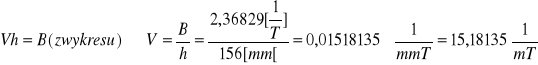
Błąd wyliczenia stałej Verdeta:
Ponieważ nie wiemy jakim przyrządem pomiarowym została zmierzona długość pręta szklanego przyjmujemy że błąd ten jest zerowy, błąd wartości ![]()
cały błąd liczymy metodą różniczki zupełnej:
![]()
Ostatecznie stała Verdeta:
![]()
Obliczenie wartości ![]()
:
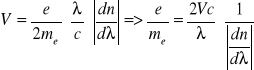
gdzie: me - masa elektronu, c - prędkość światła, ![]()
- zmiana współczynnika załamania względem długości fali.
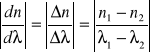
gdzie: n1, n2-współczynniki załamania fal λ1 i λ2, pomiędzy którymi leży fala światła lampy sodowej
λ światła lampy sodowej wynosi ![]()
dla λ2=0,4![]()
n2=1,53 a dla λ1=0,6![]()
n1=1,515, zatem
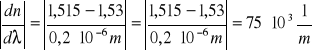
a zatem ![]()
: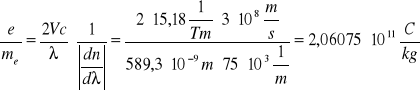
Wnioski:
Jak łatwo zauważyć z pierwszej części laboratorium sama czysta woda nie jest aktywna optycznie lecz dodanie do niej cukru powoduje pojawienie się aktywności optycznej która co więcej rośnie liniowo wraz ze wzrostem stężenia cukru w wodzie. Dzięki liniowości możemy wyznaczyć skręcenie właściwe dla danego roztworu z dość duża dokładnością. Dzięki poznaniu skręcenia właściwego dla danego roztworu mogliśmy obliczyć stężenie cukru ze znanych parametrów wartość otrzymana to 0,231±0,011 natomiast wartość oczekiwana to 0,246 czyli wartość jest bardzo zbliżona.
Z drugiego ćwiczenia spokojnie możemy stwierdzić ze prawdziwe jest prawo Faradaya, oznacza to że w polu magnetycznym niektóre ciała które w normalnych warunkach nie są aktywne optycznie stają się aktywne. W tym przypadku również występuje zależność liniowa pomiędzy prądem I[A] a skręceniem płaszczyzny polaryzacji. Z zależności kąta od indukcji magnetycznej B można obliczyć stała Verdeta. Dzięki stałej Verdeta można obliczyć stosunek ładunku elektronu do jego masy.
Wyszukiwarka