1 ) PODSTAWOWE WŁAŚCIWOŚCI KOPALNIANEJ SIECI WENTYLACYJNEJ
Kopalniana sieć wentylacyjna w której występuje ustalony stan termiczny i dynamiczny ma następujące właściwości:
Strumień masy powietrza mi w szczelnej bocznicy sieci ( elemencie i-tym) jest wielkością niezmienną , niezależną od miejsca w tej bocznicy ( m.=idem)
Strumień masy m. w szczelnym oczku bezwęzłowym sieci jest wielkością niezmienną , niezależną od miejsca w tym oczku ( m.=idem)
Strumień masy m. w bocznicy nie szczelnej jest wielkością zmienną zależną od miejsca w tej bocznicy (m.=var)
Strumień masy m. w oczku węzłowym sieci jest wielkością zmienną zależną od miejsca w tym oczku (m.=var)
Głębokość eksploatacji we współczesnych kopalniach dochodzą do kilku kilometrów , np. w Afryce Południowej ponad 3000m., w Polsce -ponad 1000m.Wysokość niwelacyjna z jest zatem wielkością zmienną , zależną od miejsca w sieci wentylacyjnej (z=var)
Różnice ciśnień powietrza na różnych wysokościach z są tak duże , że wskutek ściśliwości gęstości powietrza p jest wielkością zmienną , zależną od miejsca w sieci wentylacyjnej (p=var)
Skład chemiczny powietrza i jego masa drobinowa M. w kopalnianej sieci wentylacyjnej zależą od miejsca w sieci wentylacyjnej (M.=var)
2) RÓWNANIE STANU GAZU DOSKONAŁEGO I PÓŁDOSKONALEGO
Jeśli układ zawierający ściśle określony czynnik termodynamiczny , na skutek doprowadzenia ciepła i pracy dozna odpowiedniej przemiany , przy czym zmienią się jego parametry p,T,v to doświadczalnie wykazuje ,że parametry te nie zmienia się dowolnie , lecz w ściśle określony sposób - mianowicie w dowolnym stanie równowagi termodynamicznej zachodzi związek f(p,T,v)=0 Wymieniony związek dotyczy ściśle określonego czynnika termodynamicznego nazywa się termicznym równaniem stanu . Równania określające zależność energii wewnętrznej , entalpi , entropi od termicznych parametrow stanu nazywają się kalorycznymi równaniami stanu. W każdym z tych rownań można jeden z parametrów wyrugowac za pomoca termicznego równania stanu . Tak więc energię wewnętrzną u , entalpię horaz entropię właściwą s możemy wyrazić , stosując jako niezależne parametry termiczne, ciśnienie i temperaturę
u=f1(T,p)
h=f2(T,p)
s=f3(T,p)
Jeśli w temperaturze 0oC ciśnienie czynnika termodynamicznego i jego objętość właściwa wynoszą odpowiednio p0 i v0 to zachowując stałe ciśnienie p0=idem , po podgrzaniu tego czynnika do temperatury T(K), otrzymujemy zależność :
Pv=p0v0 αT. Iloczyn p0 i v0 jest dla określonego gazu wielkością niezmienną w temperaturze 00 C możemy więc zapisać p0 v0 α=R=idem. Z powyższych równań wynika termiczne równanie stanu gazów doskonałych i półdoskonałych
P v =RT
W którym R oznacza indywidualną stałą gazową , zależną tylko od rodzaju gazu , przy czym (R) =![]()
powyższe równanie nazywane jest równaniem Clapeyrona. Po pomnożeniu obu stron równania przez liczbę kilogramów m. i uwzględnieniu związku :
V=mv otrzymujemy ostatecznie rownanie dla całkowitej objętości gazu : p v=mRT
Powyższych wzorów nie można stosować do gazów znajdujących się pod wysokim ciśnieniem lub też w temperaturze bliskiej takiej temperaturze , w której można je skroplić .Iloczyn indywidualnej stałej gazowej i masy cząsteczkowej każdego gazu doskonałego i półdoskonałego ma jednakową wartość .Wartość ta nosi nazwę uniwersalnej stałej gazowej i wynosi :
(MR)=8314,51 J/(kmol*K).
Po pomnożeniu równania pv=RT przez masę drobinową otrzymujemy : p(Mv)=(MR)T. Mnożąc z koleji równanie to przez liczbę n kilomoli gazu otrzymuje się zależność
p(n M. v)= n (MR) T ,a ponieważ m.=nM uzyskuje się więc równanie :p m. v=n (MR)T które po uwzględnieniu wzoru
V=m. v przyjmuje postać :
pV=n(MR)T
równanie to nazywa się uniwersalnym równaniem stanu gazów doskonałych i półdoskonałych
.Gęstość masy gazu w warunkach p,T, zgodnie z równaniem pv=RT wynosi : p =![]()
po podzieleniu stronami równań dotyczących dwu różnych stanów otrzymuje się tzw wzór redukcyjny określający gęstość masy :
p2=p1![]()
W podobny sposób uzyskuje się wzór redukcyjny określający objętość :
V2=V1![]()
Za pomocą tego wzoru można redukować(sprawdzać )objętość gazu do normalnych warunków termicznych:
Vn =V![]()
Wzór ten umożliwi wyrażenie ilości gazu doskonałego lub półdoskonałego w normalnych warunkach, tj. Tn=273,15K i pn=1,013 25*105N/m2
3) ROZTWORY GAZOWE - SPOSOBY CHARAKTERYZOWANIA ROZTWORÓW
Doprowadzenie do zetknięcia się dwu lub więcej różnych czynników termodynamicznych powoduje mieszanie się ich drobin . W technice , a zwłaszcza w aerologii górniczej , ma się przeważnie do czynienia z roztworami gazowymi , które niesłusznie nazywane są mieszaninami gazowymi . W jednolitych roztworach gazów doskonałych lub półdoskonałych , w których każdy składnik zajmuje równomiernie całkowitą objętość roztworu, a temperatura każdego składnika jest taka sama słuszne jest prawo Daltona , które głosi , że ciśnienie (całkowite) roztworu gazów p jest równe sumie ciśnień cząstkowych wszystkich gazów wchodzących w skład roztworu :
p=p1+ p2+....+ pn =![]()
pi
Ciśnienie składnikowe pi i-tego składnika oznacza ciśnienie , jakie zmierzyłoby się , gdyby składnik sam zajmował objętość V roztworu i gdyby jego temperatura była równa temperaturze T roztworu .
Skład roztworu gazowego można określić trzema sposobami : za pomocą udziałów objętościowych , masowych i kilomolowych .
Udział objętościowy i-tego składnika wyraża się przez stosunek :
ri =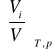
gdzie Vi- objętość składnika pod ciśnieniem p i w temperaturze T, zwana objętością składnikową ,
V-objętość roztworu w tych samych warunkach termicznych
Po skojarzeniu wzoru
Vi=![]()
z zależnością
pi =![]()
i po uwzględnieniu zależności
ri=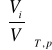
otrzymuje się :
pi = ri p z wzoru tego wynika , że ciśnienie składnikowe pi dowolnego składnika w roztworze gazowym równa się iloczynowi jego udziału objętościowego ri i ciśnienia roztworu p
Udział masowy i- tego składnika wyraża się wzorem :
gi=![]()
gdzie mi - ilość masy składnika , przy czym :
m.=m1+m2+.....+mn = ![]()
, oznacza całkowitą masę roztworu . Ponadto zachodzi zależność
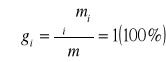
co oznacza , że suma udziałów kilogramowych jest równa jedności
Udział kilomolowy i- tego składnika jest określony stosunkiem ni (kmol) składnika do całkowitej ilości n (kmol) roztworu :
Zi =![]()
oczywiście suma udziałów molowych jest równa jedności .
Dla i-tego składnika roztworu równanie pV=m. RT ma postać :
piV=mi RiT po podzieleniu równania przez pV=m. RT otrzymujemy związek
![]()
który jest równoważny zależności :
ri=gi![]()
ponieważ zachodzi następujący związek : MiRi=(MR)=const, zależność tę można więc zapisać następująco : ri=gi![]()
, Mi i Ri oznaczają odpowiednio masę drobinową i stałą gazowa i-tego składnika roztworu , natomiast M. i R -masę drobinową i stałą gazową roztworu . Powyższe równanie umożliwia przeliczanie udziałów masowych na objętościowe i przeciwnie .
Przy stosowaniu równania pV=n(MR)T do i-tego składnika roztworu otrzymujemy :
pi V=ni (MR)T z podzielenia tego równania przez równanie wcześniejsze wynika :
![]()
czyli ri=zi ,co oznacza ,że udział objętościowy i molowy składnika w roztworze gazów doskonałych lub półdoskonałych wyraża ta sama liczba
4) POWIETRZE KOPALNIANE I JEGO WŁAŚCIWOŚCI (POWIETRZE SUCHE ,POWIETRZE WILGOTNE )
Powietrze atmosferyczne jest roztworem rożnych gazów chemicznie obojętnych wzglendem siebie , wśród których przeważają :azot , tlen , argon , i dwutlenek węgla .
Powietrze suche jest to powietrze atmosferyczne z którego usunięto parę wodną .Skład powietrza suchego jest następujący:
TLEN(O2)-20,93 %
AZOT(N2)-78,10 %
ARGON(Ar)-0,9325 %
DWUTLENEK WĘGLA(CO2)-0,03 %
WODÓR(H2)-0,01 %
NEON(Ne)-0,0018 %
HEL(He)-0,0005 %
KRYPTON(Kr)-0,0001 %
KSEON(Xe)-0,000009 %
Masa drobinowa Ma powietrza suchego i jego indywidualna stała gazowa Ra wynoszą
M.a=28,97=idem
Ra=287,04 J/(kg*K)=idem
Zawartość pary wodnej w powietrzu atmosferycznym jest zmienna , przy czym w naszym klimacie jej udział objętościowy zmienia się od 0,08 do 2,5 %. W powietrzu występują także zanieczyszczenia gazowe i pyłowe .
Powietrze kopalniane jest roztworem powietrza atmosferycznego i gazów wydzielających się w kopalni . Zgodnie z przepisami górniczymi powietrze w wyrobiskach kopalnianych , w których przebywają lub mogą przebywać ludzie powinno zawierać co najmniej 19%(objętościowo) tlenu oraz co najmniej 1%(objętościowo) dwutlenku węgla . Zawartość szkodliwych dla zdrowia gazów w powietrzu świeżym nie powinna przekraczać następujących wartości :
TLENEK WĘGLA(CO)-0,0026%
DWUTLENEK AZOTU(NO2)-0,00026%
DWUTLENEK SIARKI(SO2)-0,00075%
SIARKOWODÓR(H2S)-0,0007%
Zawartość metanu (CH4)w powietrzu świeżym nie powinna natomiast przekraczać 0,5%.W praktyce kopalnianej powietrze przepływające wyrobiskiem górniczym jest w rzeczywistości roztworem powietrza suchego i wody , czyli powietrzem wilgotnym . Woda w powietrzu może występować w trzech stanach skupienia ,tj. w stanie lotnym , ciekłym i stałym . W razie występowania w powietrzu wilgoci w stanie ciekłym , tj. zawieszonych w tym powietrzu cząstek wody , mamy do czynienia z powietrzem zamglonym . Jeśli w powietrzu występuje woda w stanie stałym , to w powietrzu występuje szron. W temperaturze i ciśnieniu powietrza występujących w kopalniach podziemnych może następować kondensacja pary wodnej ,a także odparowanie mgły .Parametrem stanu wilgotnego powietrza jest tzw .zawartość wilgoci
![]()
![]()
gdzie ;
mH2O-masa pary wodnej , kg
m.a-masa powietrza suchego, kg
5) WYKRES h-x MOLLIERA DLA POWIETRZA WILGOTNEGO
Na wykresie tym entalpia jest określona dla mieszaniny 1kg powietrza suchego oraz Xkg pary wodnej . Osie wykresu tworzą ze sobą kąt 1350 . Na wykresie naniesione są zwykle siatki linii X=idem , h=idem , t=idem , oraz φ=idem . Linia φ=1jest najważniejszą linią stałej wilgotności względnej. Linia ta dzieli wykres na dwie części . Powyżej tej lini mamy obszar powietrza nie nasyconego wilgocią(para wodna przegrzana ). Poniżej tej linii leży obszar mgły , w którym para wodna znajduje się w powietrzu w postaci kropelek . Na krzywej nasycenia są podane wartości temperatury mokrej , przy czym w punkcie przecięcia z krzywą nasycenia t=tφ (temperatura punktu rosy).Z punktów tych prowadzi się izotermy wilgotne równoległe do linii jednakowych entalpii. Punkty przecięcia się izoterm wilgotnych i suchych określają wilgotność względną powietrza. Wykres h-X jest słuszny tylko dla pewnej określonej wartości ciśnienia powietrza , gdyż φ zależy od tego ciśnienia .Wartość ciśnienia powietrza przyjęta przy sporządzaniu wykresu jest zwykle na nim podana .
6) ZASADA ZACHOWANIA ILOŚCI MASY
Wszelkie badania termodynamiczne zjawisk , opierają się głównie na zestawieniu bilansów ilości materii i energii . Każdy z wymienionych bilansów odnosi się do układu ciał , który wyodrębnia się w myśli za pomocą osłony diabatycznej , tj. kontrolnej osłony , która przepuszcza zarówno materię , jak i energię . Bilans materialny jest wyrazem tzw. Zasady zachowania materii , przyczym zachodzi związek :
m.d=∆m.u+m.w
Ilość materii m.d doprowadzonej do układu , przyrost ilości materii ∆m.u w układzie i ilość materii wyprowadzonej m.w muszą dotyczyć tego samego odcinka czasu i muszą być wyrażone za pomocą takiej jednostki uniwersalnej , tzn. kilograma. Równanie jest słuszne również wtedy , gdy użyje się kilomola lub metra sześciennego w warunkach normalnych.
7) PRZEPŁYW POWIETRZA W BOCZNICY SIECI WENTYLACYJNEJ (RÓWNANIE PRZEPŁYWU)
Równanie określające jednowymiarowy ustalony przepływ powietrza w bocznicy sieci wentylacyjnej może być wyprowadzone na podstawie bilansu energii , zestawionego dla odcinka bocznicy , ograniczonego dwoma nieskończenie blisko siebie położonymi przekrojami A i(A+dA). Przyjmujemy , że entalpia właściwa czynnika w przekroju A wynosi h , jego prędkość średnia w , środek pola A leży na wysokości z . W przekroju sąsiednim (A+dA) oddalonym o element drogi ds. odpowiednie wielkości wynoszą : (h+dh), (w+dw) oraz (z+dz). Do masy powietrza , zawartej między przekrojami I i II dopływa ciepło dq o które są uboższe źródła zewnętrzne . Powietrze zawarte między wymienionymi przekrojami nie wykonuje natomiast żadnej pracy zewnętrznej . Zestawiając bilans układu , objętego osłoną diabatyczną ograniczamy się do czasu ∆τ , potrzebnego na to , aby jednostka masy powietrza , tj. 1kg mineło przekrój I a następnie przekrój II . Równanie ruch gazów (cieczy ) rzeczywistych w szczelnych przewodach , w których nie występują opory lokalne i źródła energii ma postać :
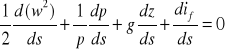
![]()
Jeśli w przewodzie występuje opór miejscowy oraz źródło energii mechanicznej , to równanie ruchu przyjmuje postać:
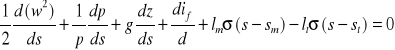
![]()
Wyszukiwarka