|
Ćwiczenie 33 Pomiar napięcia powierzchniowego |
Data pomiarów: 21.11.2006 R. |
Prowadzący:
|
WSTĘP TEORETYCZNY:
Między cząsteczkami cieczy występują siły wzajemnego oddziaływania. Siły te działają wokół każdej cząsteczki w pewnym obszarze, zwanym sferą działania. Średnie odległości cząsteczek w cieczach są znacznie mniejsze niż w gazach i dlatego siły oddziaływania między cząsteczkami cieczy są o wiele większe niż gazu. Na cząsteczkę znajdującą się wewnątrz cieczy działają siły przyciągania pochodzące od otaczających ją cząsteczek. Ze względu na symetrię sferyczną siły te kompensują się tak, że ich wypadkowa równa się zeru. Rozkład sił działających na cząsteczkę znajdującą się na powierzchni cieczy jest inny. Siły przyciągania pochodzące od cząsteczek cieczy tworzą wypadkową, która jest skierowana do wnętrza cieczy. Wypadkowa siła działająca na cząsteczki znajdujące się na powierzchni cieczy jest skierowana w głąb cieczy. Na skutek tego powierzchnia cieczy kurczy się. Gdy na ciecz nie działają siły zewnętrzne, przyjmuje kształt kuli, tzn. kształt, dla którego stosunek powierzchni do objętości jest najmniejszy. Przeniesienie cząsteczek z wnętrza na powierzchnię cieczy związane jest z wykonaniem pracy przeciw wypadkowej sił międzycząsteczkowych.
Napięciem powierzchniowym σ danej cieczy na granicy z inną fazą nazywamy pracę potrzebną do izotermicznego zwiększenia powierzchni cieczy o jednostkę. Napięciem powierzchniowym σ nazywamy także siłę styczną do powierzchni cieczy, działającą na jednostkę długości obrzeża powierzchni cieczy.
W układzie SI wymiarem napięcia powierzchniowego σ jest J/m2 lub N/m.
Na granicy cieczy oraz gazu lub ciała stałego obserwuje się zakrzywienie powierzchni cieczy, zwane meniskiem. Menisk jest wynikiem rozkładu sił, które działają na cząsteczki cieczy znajdujące się w pobliżu granic trzech faz: cieczy, gazu i ciała stałego. Siłami kohezji nazywamy siły działające między cząsteczkami tego samego ciała. Siłą adhezji nazywamy siłę działającą między cząsteczkami różnych ciał. Na przykład na cząsteczkę znajdującą się na powierzchni cieczy i w pobliżu ścianki naczynia (ciała stałego) będą działały siły pochodzące od innych cząsteczek cieczy, cząsteczek ciała stałego i cząsteczek gazu.
Oznaczmy kąt pomiędzy ścianką naczynia a powierzchnią cieczy na styku z ciałem stałym przez γ. Jeżeli napięcie powierzchniowe na powierzchni granicznej ciecz-gaz oznaczymy przez σ12, na powierzchni granicznej ciecz - ciało stałe σ13 oraz na powierzchni granicznej gaz - ciało stałe przez σ23, możemy ustalić związek między tymi wielkościami, który przedstawia się następująco: cos γ = (σ23 - σ13) / σ12 .
Jeżeli napięcie σ23 > σ13, to γ < π/2,wtedy menisk jest wklęsły i zachodzi przypadek zwilżania ścianek naczynia. Jeżeli natomiast napięcie σ23 < σ13, to γ > π/2 menisk jest wypukły i zachodzi przypadek braku zwilżania.
Dzięki istnieniu napięcia powierzchniowego pod zakrzywiona powierzchnią cieczy działa dodatkowe ciśnienie. Według Laplace'a to dodatkowe ciśnienie określa wzór:
Δp= σ (1/R1 + 1/R2),
gdzie: R1 i R2 - promienie krzywizny prostopadłych względem siebie przekrojów normalnych, dla których promienie krzywizny przyjmują wartości ekstremalne. Promienie R1 i R2 uważamy za dodatnie, gdy środki krzywizn przekrojów normalnych znajdują się po stronie cieczy, za ujemne zaś, gdy są po stronie przeciwnej.
W związku z tym dla menisku wklęsłego Δp<0, a dla menisku wypukłego Δp>0. Dodatkowe ciśnienie jest zawsze skierowane w kierunku środka krzywizny menisku. Gdy R1=R2=R (wycinek powierzchni kuli), wtedy Δp = 2σ / R. Takie jest dodatkowe ciśnienie wewnątrz pęcherzyka gazu o promieniu R, gdy znajduje się on tuż pod powierzchnią cieczy. W cienkich kapilarach dodatkowe ciśnienie pod zakrzywioną powierzchnią powoduje wznoszenie się cieczy, gdy menisk jest wklęsły (zwilżanie) i opadanie cieczy gdy menisk jest wypukły (brak zwilżania).
POMIAR NAPIĘCIA POWIERZCHNIOWEGO METODĄ ODRYWANIA.
Pomiary i wyniki dla pierwszej blaszki:
l - długość krawędzi płytki
Q - ciężar płytki
F1 - siła oderwania płytki w wodzie destylowanej
F2 - siła oderwania płytki w denaturacie
Q |
ΔQ |
F1 |
Δ F1 |
F2 |
ΔF2 |
[mG] |
[mG] |
[mG] |
[mG] |
[mG] |
[mg] |
316 |
2 |
550 |
2 |
458 |
2 |
318 |
2 |
558 |
2 |
462 |
2 |
318 |
2 |
566 |
2 |
464 |
2 |
316 |
2 |
568 |
2 |
460 |
2 |
318 |
2 |
566 |
2 |
464 |
2 |
319 |
2 |
582 |
2 |
466 |
2 |
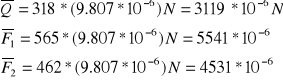
![]()
l = 18.9 [mm] = 0,0189 [m]
Δl = 0,1 [mm]
Napięcie powierzchniowe obliczymy ze wzoru:
σ = (F-Q) / 2 (l+d)
Zakładamy że d=0 dla naszej płytki i otrzymujemy w rezultacie:
σ = (F-Q) / 2l
Obliczenia dla wody destylowanej:
![]()
≈ 0.0641 [N/m]
Błąd napięcia powierzchniowego obliczmy metodą różniczki zupełnej:
Δσ = (ΔF+ΔQ)/ 2l + ((F-Q) / 2. l2). Δl
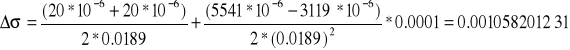
≈0.0011
Obliczenia dla denaturatu:
= 0.03735449735 ≈ 0.0374 [N/m]
![]()
Δσ = 0.001255843901 ≈ 0.0013
Napięcie powierzchniowe wynosi:
Wody destylowanej σ = (64.1 + 1.1)*10-3 [N/m]
Denaturatu σ = (37.4 + 1.3)*10-3 [N/m]
Pomiary i wyniki dla drugiej blaszki:
l - długość krawędzi płytki
Q - ciężar płytki
F1 - siła oderwania płytki w wodzie destylowanej
F2 - siła oderwania płytki w denaturacie
Q |
ΔQ |
F1 |
Δ F1 |
F2 |
ΔF2 |
[mG] |
[mG] |
[mG] |
[mG] |
[mG] |
[mg] |
352 |
2 |
614 |
2 |
486 |
2 |
350 |
2 |
598 |
2 |
494 |
2 |
350 |
2 |
586 |
2 |
488 |
2 |
352 |
2 |
584 |
2 |
486 |
2 |
350 |
2 |
572 |
2 |
486 |
2 |
350 |
2 |
586 |
2 |
488 |
2 |
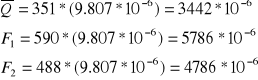
l = 19 [mm] = 0.019 [m]
Δl = 0,1 [mm]
Obliczenia dla wody destylowanej:
σ = 0.06168421053 ≈ 0.0617 [N/m]
Δσ = 0.001377285319 ≈ 0.0014
Obliczenia dla denaturatu:
σ = 0.03536842105 ≈ 0.0354 [N/m]
Δσ = 0.001238781163 ≈ 0.0013
Napięcie powierzchniowe wynosi:
Wody destylowanej σ = (61.7 + 1.4)*10-3 [N/m]
Denaturatu σ = (35.4 + 1.3) *10-3 [N/m]
II. POMIAR NAPIĘCIA POWIERZCHNIOWEGO METODĄ PĘCHERZYKOWĄ.
Urządzenie do pomiaru napięcia powierzchniowego metodą pęcherzykową przedstawiono na rysunku. Jeżeli z naczynia 1 przez zawór 2 będzie wypływać woda, to ciśnienie w zbiornikach 1 i 3 będzie się zmniejszać. W pewnej chwili u wylotu kapilary 4, który znajduje się tuż pod
powierzchnią badanej cieczy, zaczną się tworzyć pęcherzyki powietrza. Dolny koniec kapilary 4 jest zakończony stożkowo, tak że otwór kapilary i tworzące stożka stanowią ostrą krawędź. Promień pecherzyka R jest równy promieniowi kapilary r. Ciśnienie wewnątrz pęcherzyka jest równe ciśnieniu atmosferycznemu pa . Ciśnienie to jest równoważone przez
ciśnienie po-chodzące od napięcia powierzchniowego cieczy 2σ / r oraz ciśnienia pw , panującego wewnątrz naczynia 3, zatem
![]()
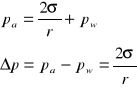
Wartość pa - pw można obliczyć na podstawie różnicy poziomów cieczy w manometrze 5
![]()
Gdzie ρT jest gęstością cieczy w manometrze. Zatem
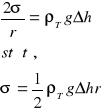
Aby był spełniony warunek zrównoważenia ciśnień, pęcherzyki powietrza wychodzące
z kapilary 4 powinny się tworzyć wolno. Opisana metoda może być stosowana do pomiaru napięcia powierzchniowego różnych cieczy. W ćwiczeniu mierzymy napięcie powierzchniowe wody.
h1 |
h2 |
Δh(h2-h1) |
[cm] |
[cm] |
[cm] |
17.4 |
21.2 |
3.8 |
17.7 |
21.1 |
3.4 |
17.5 |
21.0 |
3.5 |
17.2 |
21.2 |
4.0 |
17.3 |
20.9 |
3.6 |
17.5 |
21.3 |
3.8 |
![]()
Napięcie powierzchniowe obliczamy ze wzoru:
σ = ½ ρTg*Δh*r
ρT - gęstość wody destylowanej 998,099 + 1 [kg / m3]
r - promień kapilary (3.95 + 0.05)*10-4 [m]
g- przyspieszenie ziemskie przyjmujemy (9.81 + 0.01) [m/s2]
σ = ½ * 998.099* 9.81*3.69*10-2 *3.95*10-4 = 0.07135691963 [N/m]
Błąd pomiaru wyznaczymy za pomocą różniczki logarytmicznej:
Δσ = ( Δg /g + ΔρT /ρT + Δ(Δh) /Δh + Δr /r ). σ
Δg = 0.01 [m/s2]
ΔρT = 1[kg/m3]
Δ(Δh) = 0.001[m]
Δr = 0.05*10-4
![]()
![]()
σ ≈ (71.4 + 3.0)*10-3 [N/m]
Wnioski:
Do pomiaru napięcia powierzchniowego metodą odrywania posłużyły nam dwie metalowe płytki. Wyciągając płytkę z cieczy trzeba użyć pewnej siły, która potrzebna jest do oderwania płytki od powierzchni cieczy. Siłę potrzebną do oderwania płytek, jak i ich ciężar zmierzyliśmy wagą torsyjną. Czynności te powtórzyliśmy kilka razy w celu wyznaczenia błedu pomiaru. Znając wartości wyżej wymienionych wielkości oraz długość płytek można wyznaczyć napięcie powierzchniowe, które wynosi:
σ = (35.4 + 1.3). 10-3 [N / m] - dla denaturatu
σ = (61,7 + 1,4). 10-3 [N / m] - dla wody destylowanej.
W ocenie błędu pomiaru napięcia powierzchniowego powyższą metodą posługujemy się wzorem na różniczkę zupełną. Przy błędach wielkości mierzonych przyjmujemy, że: błąd bezwzględny Δl = 0.1 mm, czyli wartość działki elementarnej na suwmiarce. Błąd ΔF i ΔQ wynosi zaś 1 działkę na bębnie, tj. 2mG.
Metodą pecherzykową mierzyliśmy napięcie powierzchniowe wody. Przy wyznaczeniu błedu pomiaru posłużyliśmy się metodą różniczki logarytmicznej, Błąd zależy głównie od pomiaru Δh, czyli różnicy poziomu cieczy. Porównując otrzymane w ćwiczeniu wartości napięcia powierzchniowego (dla wody destylowanej) z podanymi w tablicach:
σ = (61,7 + 1,4). 10-3 [N / m] - metoda odrywania
σ = (71.4 + 3.0 ). 10-3 [N / m] - metoda pęcherzykowa
σ = 72,8. 10-3 [N / m] - wartość tablicowa
Z tych wartości można powiedzieć, że otrzymane przez nas wyniki zachowują rząd wielkości i same wartości też są zbliżone do tablicowych. Otrzymane rezultaty wskazują na stosowanie poprawnych metod pomiarowych. Jednak nie jesteśmy w stanie uwzględnić wszystkich czynników wpływających na błąd pomiarów. Na pewno wielki wpływ na błąd ma fakt, że pomiar dokonywały trzy różne osoby, które zapewne mają różne punkty widzenia.
![]()
![]()
Wyszukiwarka