Marcin Kędzierski Wrocław 30.03.98
LABORATORIUM FIZYKI OGÓLNEJ
SPRAWOZDANIE Z ĆWICZENIA NR 85
TEMAT: DYFRAKCJA FALI ŚWIETLNEJ NA FALI ULTRADŹWIĘKOWEJ.
I.CEL ĊWICZENIA.
zapoznanie z mechanizmem powstawania akustooptycznej siatki dyfrakcyjnej i ugięcia fali świetlnej na tej siatce
wyznaczenie prędkości dźwięku w cieczach
II.OPIS TEORETYCZNY.
Fala ultradźwiękowa jest to fala akustyczna o częstotliwości większej niż 20 kHz. Przechodząca przez ośrodek optyczny fala akustyczna powoduje powstanie w nim akustooptycznej siatki dyfrakcyjnej. Siatka dyfrakcyjna jest to szereg wzajemnie
równoległych i leżących w równych odstępach szczelin. Odległość między szczelinami nazywa się stałą siatki. Spójna wiązka światła przechodząc przez dwie jednakowe szczeliny ulega ugięciu i daje dwie fale spójne interferujące ze sobą. Na ekranie umieszczonym w pewnej odległości od siatki możemy zaobserwować jasne i ciemne prążki interferencyjne. Maksima promieni ugiętych obserwuje się jako jasne paski. Następuje to wtedy, gdy między promieniami wychodzącymi z dwóch sąsiednich szczelin różnica dróg wynosi kλ.
Równanie siatki dyfrakcyjnej ma postać: d sinΘk=k λ ,gdzie d-sta³a siatki (odległość między sąsiadującymi szczelinami),Θ-kąt jaki tworzy kierunek promienia ugiętego z normalną do powierzchni siatki, k- rząd widma (1,2,3...), λ- długość fali świetlnej.
Przedstawiony efekt akustooptyczny i związane z nim ugięcie fali świetlnej na powstałej dzięki temu efektowi akustooptycznej siatce dyfrakcyjnej znajduje zastosowanie w optycznych modulatorach , czy też układach sterujących wiązką świetlną przechodzącą przez siatkę akustooptyczną.
Efekt akustooptyczny polega na tym ,że przechodząca przez dany ośrodek optyczny fala akustyczna wywołuje w nim zmiany jego własności optycznych, w szczególności zmiany współczynnika załamania. Jest to spowodowane tym, że fala akustyczna jako fala mechaniczna powoduje w ośrodku sprężystym sinusoidalne zaburzenia rozkładu gęstości tego ośrodka , a ponieważ współczynnik załamania ośrodka zależy od jego gęstości , również jego rozkład będzie zmodulowany rozkładem fali akustycznej. Powstanie w ten sposób akustooptyczna siatka dyfrakcyjna o stałej d obliczonej z zależności V=λ f, gdzie V- prędkość fali dźwiękowej w cieczy, λ- długość fali dźwiękowej jest równa d, f- częstotliwość. Znając f , λ wyznaczamy z równania siatki dyfrakcyjnej zastępując sinΘ, tanΘ (ponieważ kąty ugięcia są bardzo małe)
![]()
Zmieniając równanie siatki tanΘm=xm/z (z- odległość siatki akustooptycznej od ekranu, xm- odległość m-tego prążka zerowego). Wstawiając to równanie i równanie siatki do V=λ f, otrzymujemy wzór na prędkość dźwięku:
III.PRZEBIEG ĆWICZENIA.
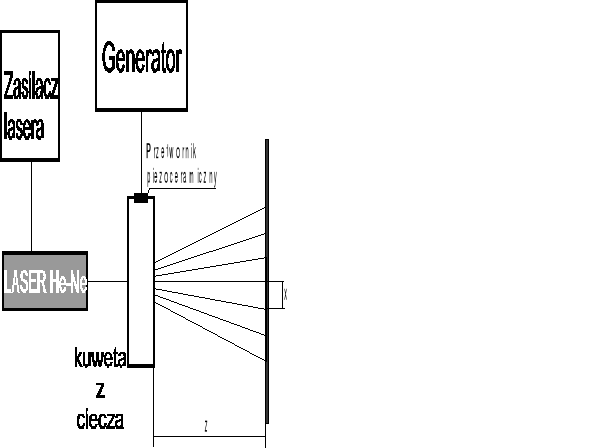
UKŁAD POMIAROWY
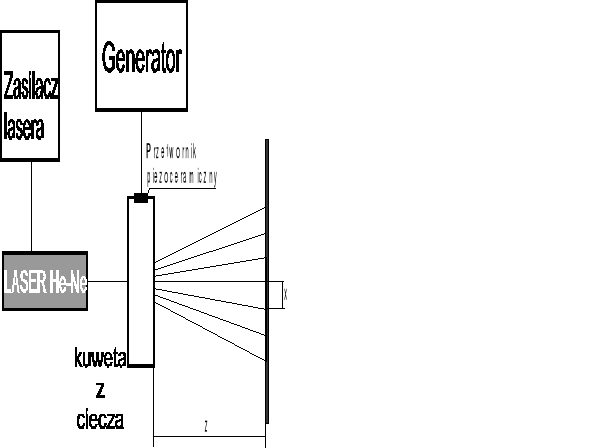
TABELA POMIAROWA
x [m] |
0,008 |
0,018 |
0,026 |
0,035 |
0,044 |
0,052 |
Δx [m] |
0,5*10-3 |
|||||
δx [%] |
6,2 |
2,8 |
1,9 |
1,4 |
1,1 |
1,0 |
z [m] |
3,76 |
|||||
Δz [m] |
0,1 |
|||||
δz [%] |
2,7 |
|||||
λLASERA [m] |
0,6328*10-6 |
|||||
f [Hz] |
5,5*10-6 |
|||||
V [m/s] |
1636 |
1454 |
1510 |
1496 |
1487 |
1510 |
δV [%] |
8,9 |
5,4 |
4,6 |
4,1 |
3,8 |
3,6 |
ΔV [m/s] |
145,7 |
79,1 |
69,2 |
61,2 |
56,5 |
54,7 |
WARTOŚĆ ŚREDNIA: V=1492 ±53 [m/s] |
||||||
Wykonano pomiar dla f=9 [MHz] (9*10-6 Hz).Inne dane pozostały niezmienione.
Zmierzono x=14 [mm] (0,014 m) z błędem bezwzględnym Δx=0,5*10-3 [m].
Obliczono V=1530 ±96 [m/s].
Rachunek błędów i przykładowe obliczenia.
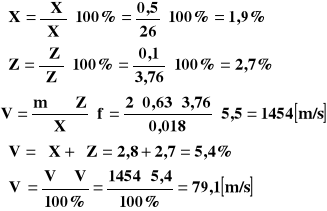
Błędy zostały policzone metodą różniczki logarytmicznej.
Sprawdzenie jednostek: ![]()
IV.DYSKUSJA BŁĘDÓW I WNIOSKI.
1
2
![]()
Wyszukiwarka