PODSTAWY STEROWANIA ROBOTÓW I MASZYN
INTERPOLACJA
Piotr Koczur
gr. 3 sem. 1 AiR
Spis treści:
Wprowadzenie do zagadnienia.
Dane do zadania.
Rozwiązanie zadania
Wnioski
1. Wprowadzenie do zagadnienia.
W wyniku realizacji algorytmu sterującego napędem robota nastepuje przemieszczenie sie każdego z napedów łańcucha kinematycznego zgodnie z okreslonym wektorem przemieszczenia, co w konsekwencji daje przemieszczenie końcówki robota do zaprogramowanego miejsca. Tor rzeczywisty często nie pokryma się dokladnie z kształtem toru zaprogramowanego, szczególnie gdzy trajektoria ruchu robota jest sumą kilku odcinków realizowanych naprzemiannie z interpolacją po prostej i po okręgu. Jest to wynikiem faktu, że zmiany kształtu trajektorii nie zachodzą w sposób ciagły. Po każdym odcinku trajektorii robota nastepuje chwilowe zatrymanie po którym nastepuje natychmiastowe przejście do nastepnego odcinka drogi robota. Odwzorowanie programowanej drogi nie jest zatem płynne i cząsto nie pokrywa się z torem zadanym. Różnice są konsekwencją konieczności dokonywania ciągłych pomiarów jakości odwzorowywania drogi zadanej. Odchyłki są odchyłkami dynamicznymi, gdyż ich wartości nie mogą przekraczać wartości dopuszczalnej.
określonej dokładnością algorytmu sterowania (błąd odwzorowywania trajektorii).
W nowoczesnych układach błąd ten wynosi 0.1mm co jest wartością zupelnie wystarczajacą dla typowych zastosowań technologicznych.
Specjalny blok programowy „interpolator trajektorii” służy do określania współrzednych pośrednich toru manipulatora tzn. pozycji podporowych gwarantujących zachowanie odpowiedniego ksztaltu trajektorii.
Interpolator oblicza współrzędne punktów pośrednich n0, n1, n2,…,na, trajektorii zgodnie z zadanym wzorcem drogi robota.
Tor przemieszczania się końcówki robota (rzeczywisty), nie pokrywa się (najczęściej) z torem określonym w programie. Tor wzdłuż którego przemieszcza się końcówka robota, jest konsekwencją przemieszczania się każdego z napędów łańcucha kinematycznego, które jest zgodne z wektorem przemieszczenia, który jest wynikiem realizacji algorytmu sterującego według określonych wartości sterowniczych związanych z ruchem robota.
Fakt iż tor rzeczywisty po którym przemieszcza się końcówka robota nie pokrywa się z torem określonym w programie widać wyraźnie gdy trajektoria zawarta w programie jest sumą kilku odcinków (np. interpolowanych naprzemiennie „po prostej” i „po okręgu”) a to dlatego że po każdym odcinku następuje bardzo krótkie zatrzymanie się robota, w celu sprawdzenia położenia względem punku docelowego. Po chwilowym zatrzymaniu się końcówki robota następuję natychmiastowe przemieszczenie się do następnego punktu. Dlatego też odwzorowanie toru zaprogramowanego nie jest płynne i nie pokrywa się dokładnie z torem zadanym.
Różnice są konsekwencją konieczności dokonywania ciągłych pomiarów jakości odwzorowywania drogi zadanej.
Odchyłki te są odchyłkami dynamicznymi, ponieważ nie mogą przekraczać wartości dopuszczalnej, określonej dokładnością algorytmu sterowania (błąd odwzorowywania trajektorii).
Bloki programowe określające pozycję pośrednie inaczej podporowe manipulatora, gwarantujące zachowanie właściwego kształtu toru nazywają się „interpolatorami trajektorii” (kształtują parametry zaprogramowanego kształtu trajektorii).
Interpolator oblicza współrzędne punktów pośrednich n0, n1, n2,…,na, trajektorii zgodnie z zadanym wzorcem drogi robota.
2. Dane do zadania.
W zadaniu występuję interpolacją „liniowa” i „kołowa”.
Natomiast występuje też interpolacja „TCP” (Tool Centered Point) która jest interpolacją punktu charakterystycznego narzędzia w której nie końcówka robota zmienia położenia, a tylko punkt charakterystyczny narzędzia zmienia orientację (rodzaj interpolacji określiliśmy w zależności od wzorca matematycznego określającego kształt drogi).
P(x,y)
x=-25
y=80
α = -35
L= 63
R=95
Φ=65
I=0.05
A=0.01
Przyjętą w projekcie jednostką miary kątowej jest stopień , natomiast długość odcinków (prosta L, promień R) wyrażone są w milimetrach [mm].
I- odchyłka dolna
A- odchyłka górna
R- promień
Φ- zakres kąta interpolacji
β- kąt pierwszego i ostatniego odcinka
α- kąt znajdujący się pomiędzy kolejnymi punktami podporowymi
3. Rozwiązanie zadania.
a. Obliczam ( α ) kąt występujący pomiędzy kolejnymi punktami
![]()
![]()
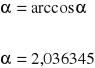
b. Obliczam ( β ) kąt pierwszego i ostatniego odcinka.
![]()
![]()
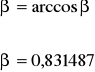
c. Obliczam ilość punktów podporowych.
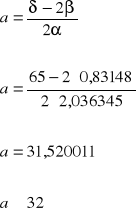
d. Obliczam ( α ) kąt pomiędzy kolejnymi punktami.
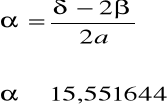
e. Obliczam współrzędne (x,y) punktów podporowych.
n |
|
|
|
0 |
2,2460 |
65 |
2,55 |
1 |
7,5526 |
64,4857 |
8,5499 |
2 |
12,8586 |
63,4187 |
14,4766 |
3 |
18,1646 |
61,8082 |
20,2792 |
4 |
23,4706 |
59,668 |
25,908 |
5 |
28,7766 |
57,0165 |
31,3148 |
6 |
34,0826 |
53,8764 |
36,4532 |
7 |
39,3886 |
50,2745 |
41,2792 |
8 |
44,6946 |
46,2418 |
45,7515 |
9 |
50,0006 |
41,8133 |
49,8312 |
10 |
55,3066 |
37,0255 |
53,4847 |
11 |
60,6126 |
31,9208 |
56,6795 |
12 |
65,9186 |
26,5426 |
59,3885 |
13 |
71,2246 |
20,9369 |
61,5885 |
14 |
76,5306 |
15,1518 |
63,2608 |
15 |
81,8366 |
9,23688 |
64,3908 |
16 |
87,1426 |
3,2428 |
64,9691 |
17 |
92,4486 |
-2,7791 |
64,9966 |
18 |
97,7546 |
-8,7435 |
64,4551 |
Koniec |
100,0012 |
-11,2972 |
64,0615 |
4. Wnioski.
Poprzez zastosowanie interpolacji możemy wyeliminować znaczące błędy powstałe w skutek krótkiego zatrzymywania się robota w celu sprawdzenia położenia końcówki robota względem punktu docelowego, po czym następuje przemieszczenie się do następnego punktu.
Zabiegi interpolacyjne pozwalają na pracę z pomijalnie małą niedokładnością. Przez co uzyskujemy dużą dokładność wytwarzania, która wpływa na jakość wyrobu a co za tym idzie większe jest zadowolenie klientów co ma bezpośredni wpływ na sprzedaż.
7
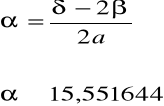
Wyszukiwarka