Nie wiem czy zadania są zrobione dobrze. Niektóre nie są zrobione do końca, wartości trzeba znaleźć w tablicach.
Czy można mówić o zależności pomiędzy terminem zbioru ziemniaka a jego trwałością w przechowywaniu, jeśli dla 393 prób otrzymano następujące zestawienie:
obliczenie wartości oczekiwanej:
obliczenie χ2
porównanie uzyskanego wyniku z wartością z tablic χ2 dla α=0,05 i df=2
Sprawdź zgodność z rozkładem normalnym cechy „zawartość tłuszczu w mleku krowim”, dla n=65, średnia próby = 4,12% i odchylenie standardowe próby = 0,43%
Oblicz prawdopodobieństwa sukcesów (pi) zawiązywania owoców róży dla liczb
ki = 0,1,2,3,4,5 , jeśli wiadomo, że 60% kwiatów róży wydaje owoce. Cecha ta posiada rozkład Bernoulliego. Przedstaw rozkład prawdopodobieństw i dystrybuanty na wykresach, oblicz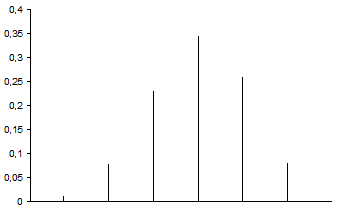
E(X) i D2(X).Własności funkcji prawdopodobieństwa i dystrybuanty zmiennej losowej skokowej. Opracuj w oparciu o przykład:
Trwałość w przechowywaniu |
Termin zbioru |
Suma |
||
|
wczesny |
optymalny |
opóźniony |
|
Dobra |
45 |
67 |
89 |
201 |
Średnia |
15 |
20 |
28 |
63 |
zła |
56 |
48 |
25 |
129 |
suma |
116 |
135 |
142 |
393 |
E= (suma wiersza *suma kolumny)/ suma ogółem
Np. dla ziemniaka o dobrej trwałości zebranego wcześnie: E= (201*116)/393= 60,21
Trwałość w przechowywaniu |
Termin zbioru |
||
|
wczesny |
optymalny |
opóźniony |
Dobra |
60,21 |
69,05 |
72,63 |
Średnia |
18,60 |
21,64 |
22,76 |
zła |
38,08 |
44,31 |
46,61 |
χ2=Σ (O-E)2/E
χ2=3,46+0,70+8,43+0,06+0,0008+0.31+3,69+1,21+10,02=27,58
χ2t=5,991
χ2obl=27,58
χ2obl> χ2t Uznajemy prawdziwość hipotezy H1- istnieje zależność między badanymi cechami.
lp |
Granice klas (xi) |
ni |
1 |
3,20-3,45 |
5 |
2 |
3,45-3,70 |
7 |
3 |
3,70-3,95 |
10 |
4 |
3,95-4,20 |
15 |
5 |
4,20-4,45 |
13 |
6 |
4,45-4,70 |
8 |
7 |
4,70-4,95 |
6 |
8 |
4,95-5,20 |
1 |
|
Suma |
65 |
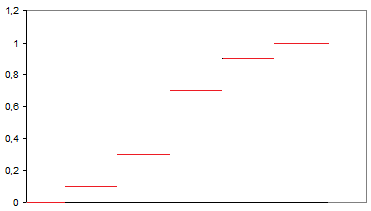
P(0; 5; 0,6)= 1 * 1 * 0,4^5= 0,01024
P(1; 5; 0,6)= 5 * 0,6 * 0,4^4=0,0768
P(2; 5; 0,6)= 10 * 0,6^2 * 0,4^3= 0,2304
P(3; 5; 0,6)= 10 * 0,6^3 * 0,4^2= 0,3456
P(4; 5; 0,6)= 5 * 0,6^4 * 0,4= 0,2592
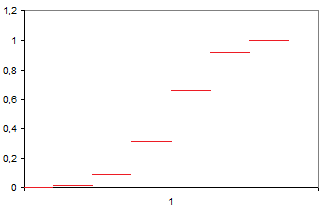
P(5; 5; 0,6)= 1 * 0,6^5 * 1= 0,07776
ΣPi=1
E(X)= 5*0,6=3,0
D2(X)= 5*0,6*0,4= 1,2
D(X)=√1,2=1,095
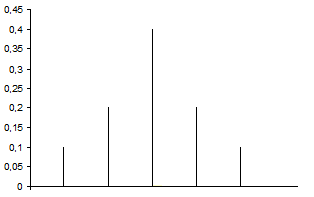
xi |
1 |
2 |
3 |
4 |
5 |
pi |
0,1 |
0,2 |
0,4 |
0,2 |
0,1 |
Oblicz: wartość oczekiwana, wariancja i odchylenie standardowe. Przedstaw na wykresie rozkład prawdopodobieństwa i dystrybuantę.
E(X)= 3,12
D2(X)= (1-3,12)2 * 0,1 + (2-3,12)2 *0,2+ (3-3,12)2* 0,4+ (4-3,12)2 * 0,2+ (5-3,12)2*0,1=0,44944+0,25088+0,00576+0,15488+0,188=1,04896
D(X)=1,0241874≈1,024
Wyszukiwarka