![]()
(13.1)
Ćwiczenie nr 13
BADANIE WŁASNOŚCI SPRĘŻYSTYCH CIAŁ
Cel ćwiczenia
Sprawdzenie prawa Hooke`a. Wyznaczenie modułu Younga .
Wprowadzenie
Podstawową cechą ciał stałych jest sprężystość postaci. Pod wpływem sił zewnętrznych ciała sztywne odkształcają się tzn. zmieniają swoje wymiary i kształt. Odkształcenie nazywamy sprężystym, jeżeli po ustaniu sił zewnętrznych ciało powraca do swojej pierwotnej postaci.
Siły zewnętrzne, które powodują odkształcenia sprężyste ciał są, zgodnie z III zasadą dynamiki, źródłem naprężeń sprężystych w odkształcanych ciałach. Wartość siły zewnętrznej F przypadającą na jednostkę pola powierzchni S ciała nazywamy naprężeniem σ:
|
(13.1) |
Jednostką naprężenia są N/m2 lub paskal [Pa], czyli jednostki ciśnienia. Naprężenie normalne występuje wówczas, gdy siła działa prostopadle do powierzchni S, a siła działająca stycznie do powierzchni powoduje naprężenia styczne.
Naprężenia wewnętrzne wywołane przez odkształcenia sprężyste są proporcjonalne do względnego odkształcenia:
|
(13.2) |
gdzie:
σ - naprężenie normalne lub styczne,
K - moduł sprężystości, który jest równy naprężeniu jeśli względne naprężenie
ε = 1(zależy od rodzaju odkształcenia)
Odkształcenie względne ε = Δx/x0 jest równe stosunkowi odkształcenia bezwzględnego Δx do początkowej wartości x0 określającej początkowe rozmiary lub kształt ciała.
Powyższe równanie nosi nazwę uogólnionego równania Hooke`a, jego szczegółowe postacie zależą od rodzaju odkształcenia.
Rozważmy pręt o długości początkowej l0, przekroju poprzecznym S rozciągany lub ściskany siłą F prostopadłą do powierzchni S. Względne wydłużenie (skrócenie) pręta Δl jest proporcjonalne do przyłożonej siły F, początkowej długości pręta l0 i odwrotnie proporcjonalnie do przekroju poprzecznego S co można zapisać wzorem:
|
(13.3) |
gdzie α oznacza współczynnik proporcjonalności (sprężystości).
Przekształcając powyższe równanie otrzymujemy:
|
(13.4) |
|
(13.5) |
|
(13.6) |
gdzie:
E - moduł Younga,
ε - naprężenie względne.
Otrzymane równanie jest zgodne z ogólnym równaniem Hooke`a. Wynika z niego, że naprężenie wewnętrzne jest proporcjonalne do względnego odkształcenia pręta. Moduł Younga określa sprężystość ciał. Jego wartość jest równa naprężeniu, które powstałoby przy dwukrotnym zwiększeniu długości ciała. Dla większości materiałów np. drutu stalowego jest to niemożliwe. Wartości modułu Younga wyznaczone doświadczalnie można znaleźć w tablicach fizycznych. Prawo Hooke`a obowiązuje tylko dla ciał sprężystych w ograniczonym zakresie. Przy wzroście działającej na ciało siły osiągamy najpierw granicę sprężystości (obowiązywania prawa Hooke`a), a następnie granicę wytrzymałości materiału.
Opis stanowiska laboratoryjnego
Wykaz urządzeń przyrządów i materiałów: statyw z uchwytem do umocowania drutu, suwmiarka z dziurką do umocowania końca drutu , śruba mikrometryczna, przymiar liniowy, szalka do zawieszania obciążników obciążniki, cienkie druty o kilku średnicach wykonane z różnych metali.
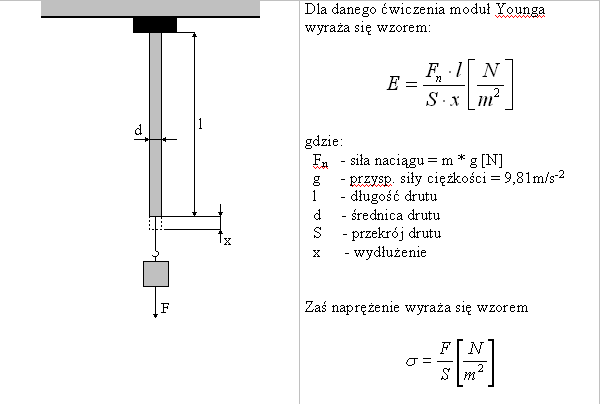
Rys. 13.1 Schemat układu pomiarowego do wyznaczania modułu Younga
Program ćwiczenia
Umieścić jeden koniec badanego drutu o długości około 1m w specjalnym uchwycie umocowanym do ściany lub ramy.
Zmierzyć śrubą mikrometryczną średnicę drutu d=2r.
Zważyć szalkę i przymocować do końca suwmiarki.
Przymocować swobodny koniec drutu do drugiego końca suwmiarki
Zmierzyć długość początkową drutu.
Określić niepewności pomiarów bezpośrednich.
Zawieszać pod szalką kolejno ciężarki o masie m = 50 g.
Obserwować i zanotować kolejne wydłużenia drutu li , Δli = li - l0 Jeżeli zauważymy duże zmiany długości zmniejszyć wartość kolejnych obciążników.
Wyniki pomiarów umieścić w tabeli 13.1.
Tabela 13.1
l0= 2r= Δl0= Δ2r= Δm= Δ(Δli)= Δx= g=9,81 m/s2
lp. |
mi[g] |
Σmi[g] |
Σmi[kg] |
li[mm] |
Δli= li-l0 [mm] |
Δli[m] |
Fi=Σmig[N] |
|
|
|
|
|
|
|
|
Sprawozdanie
Korzystając z danych pomiarowych oblicz przekrój poprzeczny drutu S=πr2,n aprężenie σ = F/S i względne wydłużenie ε = Δl/l0. Wyniki umieść w tabeli 13.2.
Tabela 13.2.
S=πr2 l0= σ=F/S=
lp. |
Fi=Σmig[N] |
σ=F/S[Pa] |
Δli[m] |
ε=Δli/l0 |
E [Pa] |
ΔE/E |
ΔE/E [%] |
|
|
|
|
|
|
|
|
Wartość modułu Younga obliczyć ze wzoru (13.7):
|
(13.7) |
Maksymalną niepewność systematyczną wyznaczenia modułu Younga wyznacz ze wzoru:
|
(13.8) |
gdzie Δl oznacza bezwzględne wydłużenie
Wyniki obliczeń ΔE/E umieścić w tabeli 13.2.
Sporządzić wykres naprężenia σ w funkcji względnego wydłużenia Δl/l0. Nanieść na wykres niepewności pomiarowe obliczone metodą różniczki zupełnej.
Sprawdzić zakres stosowalności prawa Hooke`a. W ustalonym zakresie przez prostokąty niepewności pomiarowych przeprowadzić prostą.
Obliczyć współczynnik kierunkowy prostej i wyznaczyć wartość modułu Younga.
Wyznaczoną z wykresu wartość E porównać z wartościami otrzymanymi w tabeli 13.2.Zaznaczyć, które punkty pomiarowe w tabeli 2 spełniają prawo sprężystości.
Z tablic lub Internetu znaleźć wartości modułu Younga dla badanych materiałów. Obliczyć względne różnice:
|
(13.9) |
10. Spostrzeżenia i wnioski.
Pytania kontrolne
Własności ciał stałych.
Prawo Hooke`a i granice jego stosowalności.
Rodzaje odkształceń ciał stałych.
Sens fizyczny modułu Younga i zakres wartości modułu E.
86