Granice ciągu

1. Korzystając z definicji granicy udowodnić, że:

a)
b)

2. Obliczyć granice ciągów:

a)
b)
c)

d)
e)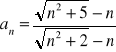
f)

g)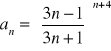
h)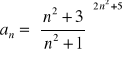

3. Wykorzystując twierdzenie o trzech ciągach wyznaczyć granice następujących ciągów:

a)
b)
c)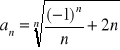

d)

4. Zbadać, czy następujące ciągi są zbieżne:

a)
b)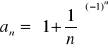

Granice i ciągłość funkcji

1. Obliczyć granice

a)
b)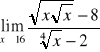
c)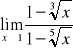

d)
e)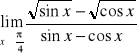
f)

g)
h)
h)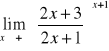

i)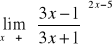

2. Obliczyć granice jednostronne następujących funkcji w podanych punktach i rozstrzygnąć, czy funkcje te mają w tych punktach granice:

a)
w punkcie
b)
w punkcie

c)
w punkcie

3. Zbadać ciągłość następujących funkcji:

a)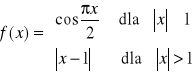
b)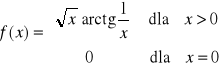

4. Niech
będzie określona następująco:

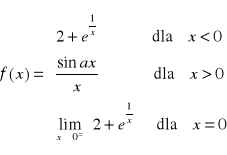
Dobrać a tak, żeby ta funkcja była ciągła na R.

1