ZESPOLONE
(def)Sprzężeniem liczby zespolonej Z=x+yi gdzie (x,y)εR nazywamy liczbę zespoloną Z=x-yi;
(def)Modułem liczby zespolonej Z=x+yi nazywamy liczbę rzeczywistą sqrt(x^2+y^2) i oznaczamy |Z|;
(def)Argumentem liczby zespolonej Z=x+yi ≠0 x,yεR nazywamy każdą liczbę rzeczywistą γεR spełniającą układ równań ![]()
. Argumentem głównym liczby zespolonej nazywamy jej argument spełniający warunek γε[0,2Π);
Postać trygo.
(def)Każdą liczbę zespoloną Z=x+yi można przedstawić w postaci Z=r(cosγ+isinγ) gdzie r≥0 γεR r=|Z| γ=ArgZ;
(tw)Dwie liczby zespolone Z1, Z2 postaci trygonometrycznej są równe Z1=|Z1|(cosγ1+isinγ1) Z2=|Z2|(cosγ2+isinγ2) Z1=Z2 ↔|Z1|=|Z2| γ1=γ2+2kΠ kεC;
(tw)Mnożenie i dzielenie liczb zespolonej postaci trygonometrycznej Z1*Z2=|Z1||Z2|[cos(γ1+γ2)+isin(γ1+γ2)] Z1/Z2=|Z1|/|Z2|[cos(γ1-γ2)+isin(γ1-γ2)];
Potęgowanie
(tw)Potęgowanie liczb zespolonych(wzór de Moiore'a) Niech Z=|Z|(cosγ+isinγ) Zn=|Z|n(cosnγ+isinnγ);
Pierwiastkowanie
(def)Pierwiastkiem stopni naturalnego n z liczby zespolonej Z nazywamy, każdą liczbę zespoloną W taką, że Wn=Z. Zbiór pierwiastków stopnia n oznaczmy ![]()
(tw)Każda liczba zespolona Z przedstawiona w postaci trygonometrycznej ma dokładnie n pierwiastków stopnia n. Zbiór tych pierwiastków ma postać ![]()
k=0,1,2,3...,n-1;
Postać wykładnicza
(def)Dla liczby rzeczywistej γ liczbę zespoloną cosγ+isinγ oznaczamy przez eiγ eiγ=cosγ+isinγ;
(tw)Wzory Eulera ![]()
![]()
;
(tw)Każdą liczbę zespoloną Z można zapisać w postaci wykładniczej Z=|Z|eiγ γεR γ=argZ
WIELOMIAMY
Wielomianem zespolonym stopnia n nazywamy funkcję W!C->C określoną wzorem ![]()
nεN∪{0}
Dzielenie wielomianów
Mówimy, że wielomian S(x) jest ilorazem a wielomian R(x) resztą z dzielenia wielomianu P(x) przez wielomian Q(x) gdy P(x)=Q(x)*S(x)+R(x), stopień reszty jest mniejszy od stopnia dzielnika. Jeżeli reszta jest wielomianem zerowym to mówimy, że wielomian P(x) jest podzielny przez wielomian Q(x);
(tw)Wielomian zespolony W(z)=az^2+bz+c a,b,cεC, a≠0 ma dwa pierwiastki zespolone ![]()
![]()
(tw)Zasadnicze tw. algebry. Każdy wielomian st. Dodatniego o wspólczynnikach zespolonych ma przynajmniej jeden pierwiastek zespolony.
(tw)1 Każdy wielomian zespolony stopnia nεN ma dokładnie n pierwiastków zespolonych (uwzględniając pierwiastki wielokrotnie). 2 niech wielomian W st. nεN ma pierwiastki zespolone Zj o krotności kj kjεN k1+k2+k3+....+kn=n wówczas ![]()
(tw) o pierwiastkach zespolonych wielomianu rzeczywistego. Niech ![]()
wówczas liczba zespolona Z0 jest k-krotnym pierwiastkiem wielomianu W(x)⇔ liczba Z0 jest k-krotnym pierwiastkiem tego wielomianu;
(tw) o rozkładzie wielomianu. Niech W(x) będzie wielomianem rzeczywistym st. nεN i niech xj j=(1,...,R) będą jego pierwiastkami rzeczywistymi o krotności kj i niech Zi, Zi Jmzi>0 będą pierwiastkami zespolonymi tego wielomianu o krotności li przy czym musi zachodzić związek k1+k2+k3+...+kr+2(l1+l2+...+ls)=n wówczas ten wielomian ![]()
pi=-2Rez qi=|Zi|^2 i=1,....,s. Każdy wielomian stopnia nieparzystego ma przynajmniej 1 pierwiastek rzeczywisty.
MACIERZE
Macierz to funkcja która parze liczb naturalnych (i,j) i,jεN przyporządkowuje pewną liczbę aij (aijεR, C);
Transpozycja
Macierzą transponowaną do macierzy A nazywamy macierz AT której zamieniono wiersze i kolumny. Macierz symetryczna - jest to macierz kwadratowa o tej własności że AT=A. Macierz asymetryczna(skośnie symetryczna) - to jest macierz kwadratowa AT=-A;
Wyznacznik
Inwersja - niech a1,a2,a3,...,an -będzie skończonym ciagiem różnych liczb rzezczywistych. Para liczb aj, ak tego ciągu tworzy inwersję gdy aj>ak dla j<k;
Minorem elementu aij macierzy kwadratowej st. n A nazywamy wyznacznik stopnia n-1 macierzy powstałej z macierzy A przez wykreślenie i-tego wiersza oraz j-kolumny;
Dopełnieniem algebraicznym Aij elementu aij jest jego minor pomnożony przez (-1)i+j
(tw)Laplace'a. Dowolny wyznacznik jest równy sumie iloczynów elementów dowolnego wiersza lub kolumny i ich dopełnień algebraicznych ![]()
;
Kombinacja liniowa- mówimy że element jest kombinacją liniową innych elementów jeżeli jest sumą iloczynów pewnej liczby przez te elementy;
Własności wyznaczników: 1. Wartość wyznacznika nie ulega zmainie, gdy w jego macierzy zmieniamy wiersza na kolumny i odwrotnie det A= det AT, 2. jeżeli 1 z kolumn wyznacznika skałada się z samych zer to wyznacznik równy jest zero, 3. przestawienie dwóch kolumn zmienia wartość wyznacznika na przeciwny, 4. jeżeli 2 kolumny są identyczne to wartość wyznacznika jest równa zero, 5. pomnożenie 1 kolumny w wyznaczniku przez liczbę jest równoważne z pomnożeniem całego wyznacznika prze tą liczbę, 6. 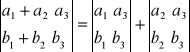
, 7. jeżeli 1 kolumna jest kombinacją liniową pozostałych to wyznacznik jest równy zero, 8. jeżeli wyznacznik jest równy zero to przynajmniej 1 z jego kolumn jest kombinacją liniową pozostałych, 9. jeżeli do pewnej kolumny w wyznaczniku dodamy kombinację liniową pozostałych to wartość wyznacznika nie ulegnie zmianie;
Wyznacznik macierzy trójkątnej jest iloczynem elementów na głównej przekątnej;
(tw)Cramera. Układ Cramera ma dokładnie jedno rozw. jest ono dane wzorem ![]()
k=1,2,...,n Ak - powstaje z macierzy A przez zastąpienie k-tej kolumny kolumną wyrazów wolnych b1,b2,...,bn. det A=0 i det Ak=0 to układ posiada nieskończenie wiele rozwiązan(nieoznaczony). detA=0 ![]()
to układ jest sprzeczny nie ma rozwiazań. Gdy ![]()
to układ niejednorodny;
(tw)Układ jednorodny (tzn bk=0 b=1,2,...,n) równań liniowych ma rozwiązanie niezerowe ⇔ wyznacznik główny jest równy zero
Macierzą odwrotna do macierzy nieosobliwej A(tzn |A|≠0) nazywamy macierz ![]()
. macierz AD jest to macierzą transponowana dopełnień algebraicznych elementów macierzy A;
(def)Rząd macierzy.1. macierz zerowa ma rząd zero. 2. jeżeli nie wszystkie elementy macierzy są zerami, ale wszystkie wyjęte z niej wyznaczniki stopnia 2 lub wyższego są równe 0, to macierz ma rząd 1. 3. jeżeli wszystkie wyznaczniki stopnia wyższego niż r wyjęte z macierzy są równe zeru, a prznajmniej jeden wyznacznik stopnia r jest różny od zera to macierz ma rząd r.
(tw)rząd macierzy nie ulega zmainie gdy:1. kolumny ppomnożymy przez liczby różne od zera. 2. przestawimy kolumny. 3. do jednej kolumny dodamy kombinacje liniowe innych kolumn(to samo dla wierszy);
(tw) kroneckera-Capelliego, Układ równań liniowych (L) jest rozwiązywalny ⇔ rzA=rzU gdy rzA=rzU=n to istnieje dokładnie jedno rozwiązanie, gdy rzA=rzU=r<n to wóczas układ (L) ma nieskończenie wiele rozwiązań zależnyhc od n-r parametrów;
W układach równań gdy m=n możemy zapisać w postaci macierzy A*X=B X=B*A-1;
FUNKCJE
Niech g=f(x) będzie różnowartościowa w przedziale [a,b] i niech przedział [c,d] będzie zbiorem wartości tej funkcji wówczas każdej yε[c,d] odpowiada dokładnie jedna wartość xε[a,b] taka, że f(x)=y. Tę wartość x oznaczamy przez g(y) zatem x=g(y) określa w zbiorze [c,d] funkcję zmiennej y. Nazywamy ją funkcją odwrotną do funkcji y=f(x);
Funkcja złożona. Dane są 2 funkcje y=f(u) u=g(x) pierwsza określona w przedziale [α,β] natomiast 2 w przedziale [a,b]. Jeżeli wartość u=g(x) należy do przedziału [α,β] to zmienną g możemy uważać jako zależną od x. Mówumy wówczas, że y jest funkcją x złożoną z funkcji y=f(u) i u=g(x) y=f(g(x)) y- funkcja wewnętrzna f- funkcja zewnętrzna;
Granica funkcji ![]()
Pochodna i różniczka
(def)Niech f będzie określona w pewnym otoczeniu punktu x0 obierzemy w tym otoczeniu dowolną liczbę x1≠x0 i oznaczymy x1-x0=Δx (x1=x0+Δx). Różnicę Δx=x1-x0 nazywamy przyrostem zmiennej x natomiast różnicę f(x1)-f(x0)=f(x0+Δx)-f(x0) nazywamy przyrostem funkcji, a iloraz przyrostu Δf/Δx=f(x1)-f(x0)/x1-x0=f(x0+Δx)-f(x0)/ Δx nazywamy ilorazem różnicowym
(def)Pochodna funkcji. Jeżeli iloraz różnicowy ma granicę przy Δx->0 (x1->x0) w punkcie x0 to tę granicę nazywamy pochodną funkcji w punkcje x0 i oznaczamy f'(x0) ![]()
;
Różniczka funkcji f(x0+Δx)=f(x0)+f'(xo)dx
Pochodne wyższych rzędów. Jeżeli funkcja jest różniczkowalna w pewnym przedziale i pochodna jest f. Różniczkowalną to jej pochodna nazywasię 2 pochodną f(x) i oznaczany f(n)(x). Funkcję f(x) mającą w przedziale [a,b] n pochodnych nazywamy n-krotnie różniczkowalną. Jeśli ponadto funkcja f(n)(x) jest ciągła to mówimy, że funkcja jest w przedziale [a,b] klasy Cn.
(tw)wzór Leibnitca. Niech f i g będą funkcjami n-krotnie różniczkowalnymi w pewnym przedziale wówczas 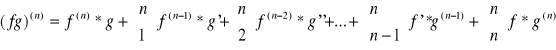
(tw)o wartości średniej Lagronge'a. Jeżeli 1. fεC[a,b], 2. fεC1(a,b) to istenieje punkt cε(a,b) taki że f'(c)=f(b)-f(a)/b-a. Wniosek 1 jeżeli f'(x)=0 dla xε[a,b] f(x)=const. Wniosek 2 Jeżeli f'(x)>0[<0] to f(x)↑[f(x)↓] w [a,b];
(tw) Rolle'a. Jeżeli 1. fεC[a,b] 2. fεC1(a,b) 3. f(a)=f(b) to istnieje cε(a,b) takie że f'(c)=0;
(tw) Taylora. Jeżeli f(x) jest klasy Cn[x0,x0+h] to istnieje punkt c=x0+θh θε(0,1) taki, że ![]()
;
(tw)Maclourina. X0=0 niech f(x) spełnia założenia Taylora h=x ![]()
;
(tw) Couchy'ego. Jeżeli 1. f,yεC[a,b] 2. f,yεC1(a,b) 3. g'(x)≠0 dla xε(a,b), to istnieje taki punkt cε(a,b) taki że f'(c) /f'(c)=f'(b)-f'(a)/g'(b)-g'(a);
(tw) reguła de L'Hospitala. Jeżeli 1. f(x), g(x) ![]()
2. jeżeli istnieje granica ![]()
to istanieje również ![]()
oraz ![]()
(tw.) to dotyczy również granic jednostronnych oraz x0 jest +∝ -∝
Symbole nieoznaczone 1. 0*∝ ![]()
2. ∝-∝ ![]()
3. 00 ∝0 1∝ ![]()
;
Maksima i minima.
(def)Mówimy, że funkcja f określona w pewnym otoczeniu x0 ma w tym pumkcie max[min] lokalne jeśli f(x0)>f(x) dla xε(x0,δ) f(x0)<f(x) dla xε(x0,δ);
(tw)warunek konieczny istnienia extremum. Jeżeli funkcja f(x) ma w punkcie x0 extermum to pochodna funkcji w tym punkcie =0 f'(x0)=0;
(tw)warunek dostateczny istnienie extremum. 1. jeżeli f'(x) zmienia znak w punkcie x0 to funkcja f ma w tym punkcie extremum lokalne dokładniej 1:f'(x)>0 dla xε(x0-δ,x0) i f'(x)<0 xε(x0,x0+δ) w punkcie x0 funkcja ma max, 2: 1:f'(x)<0 dla xε(x0-δ,x0) i f'(x)>0 xε(x0,x0+δ) w punkcie x0 funkcja ma min. 2. jeżeli pochodna w punkcie f'(x0)=0 i f''(x0)≠0 to funkcja ma w punkcie x0 extremum jest to max gdy f''(x0)>0 a min f''(x0)<0.
Ogólnie: Jeżeli f'(x0)=0 f(n-1)(x0)=0 natomiast f(n)(x0) ≠0 to wówczas gdy n jest nieparzyste to extremum nie istnieje a gdy n jest parzyste, to funkcja ma extremum w punkcie x0 i gdy f(n)(x0)>0 to w x0 jest min, a gdy f(n)(x0)<0 to w x0 jest max;
Wklęsłość, wypukłość.
(def)Funkcja jest ∪ w przedziale (a,b) gdy ![]()
f(λx1+(1-λ)x2)≤ λf(x1)+(1-λ)f(x2);
(def)Funkcja jest ∩ gdy w przedziale (a,b) ![]()
f(λx1+(1-λ)x2)≥ λf(x1)+(1-λ)f(x2);
(tw)Funkcja f(x) jest ∪ w przedziale (a,b) gdy ![]()
f''(x)>0 natomiast jest ∩ w przedziale (a,b) ![]()
f''(x)<0;
(def)Punkt (x0,f(x0)) jest punktem przegięcia wykresu funkcji f(x) gdy funkcja jest określona w punkcie i ma w nim pochodną i w przedziale (x0-δ,x0) jest wypukła[wklęsła] a w przedziale (x0,x0+δ) jest wklęsła[wypukła];
(tw)warunek konieczny istnienia punktów przegięcia. Punkt (x0,f(x0)) jest punktem przegięcia funkcji f(x) gdy f''(x0) istnieje i jest f''(x0) =0;
(tw)Warunek dostateczny istnienia punktu przegięcia. Jeżeli f'' zmienia znak w punkcie x0 to punkt o współrzędnych (x0,f(x0) jest punktem przegięcia wykresu;
CAŁKA NIEOZNACZONA
(def)Niech f(x) będzie funkcja określoną w pewnym przedziale [a,b] każdą funkcję F(x) różniczkowalną w tym przedziale [a,b] i spełniającą w nim związek F'(x)=f(x) nazywamy funkcją pierwotna funkcji f(x);
(tw)Dwie różne funkcje pierwotne F(x) i G(x) tej samej funkcji f(x) różnią się w przedziale [a,b] tylko o stałą;
(def)Całą nieoznaczoną funkcji f(x) w przedziale [a,b] nazywamy każdą jeje funkcję pierwotną ჲf(x)dx=F(x)+c;
Całkowanie przez podstawienie.
(tw)Niech f(x) będzie f. Ciągą w przedziale (ၡ,ၢ) i niech F(t) będzie f. Pierwotną tzn. ჲf(x)dt=F(t) niech ponadto t=g(x) będzie funkcją ciągłą w przedziale (a,b) spełniającą w nim nierówność ၡ<g(x)<ၢ i mającą pochodną g'(x) wówczas ჲf(g(x))*g'(x)dx=ჲf(t)dt dla t=g(x);
Całkowanie przez części
(tw)Niech U(x) i V(x) będą funkcjami mającymi w pewnym przedziale ciągłe pochodne U'(x) V'(x) wówczas ჲU(x)+V'(x)dx=U(x)*V(x)- ჲV(x)*U'(x)dx V'(x)=dV/dx U'(x)=dU/dx ჲUdV=U*V-ჲVdU;
Całkowanie funkcji wymiernych
Funkcją wymierną nazywamy iloraz dwóch wielomianów W(x)/G(x). Funkcja wymierna postaci ![]()
lub 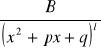
nazywa się ułamkiem prostym to k,lၥN oraz a,b,c,p,q są stałymi b2-4q<0;
![]()
mogą zajść następujące przypadki: 1. mႳn wówczas dzielimy Wm(x) przez Wn(x) ![]()
, 2. m<n iloraz Wm(x)/Wn(x) rozkładamy na sumę ułamków prostych po uprzednim rozłożeniu wielomianu Wn(x) na czynniki 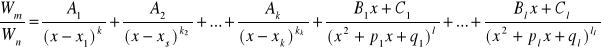
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka