Politechnika Lubelska w Lublinie	Laboratorium Teorii Obwodów
Imię i Nazwisko: Marcin Skiba Łukasz Pyra Gabriel Siłuch Wojciech Rzepka	Semestr: III	Grupa: 3.4	Rok akademicki: 2012/2013
Temat: Drgania relaksacyjne		Data wyk.: 13.12.2012r.	Ocena:

1. Cel ćwiczenia.

Celem ćwiczenia jest zapoznanie się ze zjawiskiem drgań relaksacyjnych.

2. Wykonanie ćwiczenia.

a). Badanie układu z diodą gazowaną (stabiliwoltem).

Pomiar napięcia zapłonu i gaśnięcia stabiliwoltu.

Układ do badania napięcia zapłonu i gaśnięcia stabiliwoltu.

Tabela.

Lp.	Uz	Uzśr	Ug	Ugśr
	V	V	V	V
	100,33		72,98
	100,02	99,97	72,42	72,88
	99,57		73,25

Pomiar częstotliwości drgań relaksacyjnych.

Układ do badania częstotliwości drgań relaksacyjnych.

Tabela.

Lp.	U	R	C	T	Tobl
		V	kΩ	μF	s	s
1.	102,29	330	4	4,68	3,35
2.	102,52	560	4	6,59	5,49
3.	110,08	330	4	2,04	1,72
4.	110,09	560	4	3,43	2,92
5.	102,62	330	8	8,73	6,38
6.	102,41	560	8	13,55	11,17
7.	110,01	330	8	4,16	3,45
8.	110,04	560	8	6,65	5,85

Przykładowe obliczenia

Na podstawie znanych wartości U, U_z, U_g, R, C wyznaczam okres drgań relaksacyjnych ze wzoru:

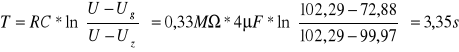
b). Badanie układu z diakiem.

Wyznaczenie charakterystyki diaka.

Układ do wyznaczania charakterystyk diaka.

Charakterystyka i aproksymacja diaka na załączniku nr 1

Wnioski

Przykładem drgań relaksacyjnych są drgania piłokształtne (lub trójkątne) uzyskiwane w generatorach przez wykorzystanie procesów ładowania i rozładowania kondensatora ze źródła napięcia stałego. Układ taki musi zawierać element ograniczający prąd ładowania kondensatora (w naszym przypadku jest to rezystor) oraz element umożliwiający przejście kondensatora z procesu ładowania do rozładowywania i na odwrót (w naszym przypadku jest to neonówka lub diak). Nasze pomiary dotyczące obliczeń okresu drgań relaksacyjnych neonówki nieznacznie się różniły, a wynikało to z refleksu przeprowadzającego pomiar, oraz z dokładności stopera.

---