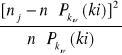LABORATORIUM FIZYKI II |
Ćwiczenie nr: 1 |
|||
Wydział: Mechatronika |
Grupa: R 39 |
Zespół: 6 |
Data wykonania: |
|
Nazwisko i imię: Żelski Krzysztof |
Ocena |
Przygotowanie: |
||
Sprawozdanie przyjęto: |
Data: |
Podpis: |
|
|
|
|
|
|
Zaliczenie |
Prowadzący: |
|
|
||
Pierwszym etapem ćwiczenia był pomiar mocy dawki pochłoniętej za pomocą radiometru RK-67. Urządzenie to pozwala na badanie mocy dawki pochłoniętej od dwóch stron: cienkościennej i grubościennej.
Wyniki pomiarów były następujące:
Od strony grubościennej licznik wskazał około 3 μGy/h
Od strony cienkościennej licznik wskazał około 1200 μGy/h
Wyniki pomiarów świadczą o tym, że promieniowanie jest bardzo mało przenikliwe. Strona grubościenna detektora powstrzymała niemal całe promieniowanie próbki. Mamy zatem do czynienia z promieniowaniem β. Promieniowanie α wykluczam (pomimo że cechuje się również bardzo słabą przenikliwością), ponieważ ma bardzo mały zasięg, a poza tym prawdopodobnie zostało by powstrzymane przez stronę cienkościenną detektora (jako osłona przed promieniowaniem tego typu starcza już kartka papieru).
Przemiana jądrowa:
Rozpatrywana w trakcie doświadczenia przemiana jądrowa jest typu β. W tego typu przemianach liczba protonów lub neutronów zmniejsza się o jeden, przy czym nadmiarowy neuklon nie jest bezpośrednio usuwany z jądra, ale ulega przemianie na neuklon innego rodzaj, a na zewnątrz emitowany jest elektron lub pozyton.
e - elektron
ν - neutrino
W drugiej części doświadczenia wyznaczyliśmy charakterystykę roboczą licznika Geigera-Mullera.
Wyniki pomiarów i wykreślony na ich podstawie wykres znajdują się poniżej (badana próbka A1):
Napięcie U [V] |
Ilość impulsów N |
Szybkość liczenia I [imp/min] |
σ=(I/t)^1/2 |
720 |
33035 |
33035 |
181,755 |
710 |
29496 |
29496 |
171,744 |
700 |
25548 |
25548 |
159,837 |
690 |
22452 |
22452 |
149,840 |
680 |
20882 |
20882 |
144,506 |
670 |
19424 |
19424 |
139,370 |
660 |
18029 |
18029 |
134,272 |
650 |
17393 |
17393 |
131,883 |
640 |
16680 |
16680 |
129,151 |
630 |
16585 |
16585 |
128,783 |
620 |
15905 |
15905 |
126,115 |
610 |
15581 |
15581 |
124,824 |
600 |
15554 |
15554 |
124,716 |
590 |
15405 |
15405 |
124,117 |
580 |
14991 |
14991 |
122,438 |
570 |
14945 |
14945 |
122,250 |
560 |
14762 |
14762 |
121,499 |
550 |
14409 |
14409 |
120,037 |
540 |
14223 |
14223 |
119,260 |
530 |
12086 |
12086 |
109,936 |
528 |
11633 |
11633 |
107,856 |
526 |
10133 |
10133 |
100,663 |
524 |
4259 |
4259 |
65,261 |
522 |
6 |
6 |
2,449 |
521 |
0 |
0 |
0,000 |
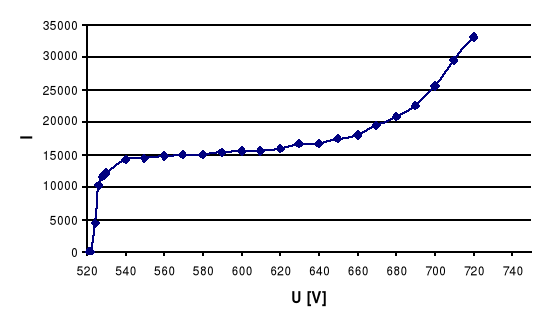
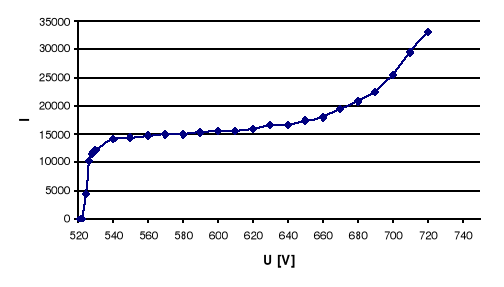
Na podstawie wykresu możemy określić podstawowe parametry licznika:
Napięcie progowe: Up=522 [V]
Napięcie pracy: U=590 [V]
Długość plateau: 100 [V]
Nachylenie plateau: 16%
Zmierzyliśmy również tło licznika: I = 15 [imp/min]
W trzeciej części doświadczenia wyznaczaliśmy czas martwy licznika. W tym celu usieliśmy dokonać trzech różnych pomiarów.
Czas trwania pomiarów: 10 minut.
Napięcie pomiarowe = napięcie pracy: 590 [V]
Próbka A1: N=149051 impulsów I1=14905,1 [imp/min]
Próbka B2,A1: N=248557 impulsów I1,2=24855,7 [imp/min]
Próbka B2: N=116205 impulsów I2=11620,5 [imp/min]
Czas martwy licznika wynosi:
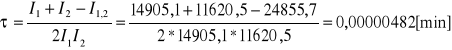
τ =0,0002892 [sek] = 289,2 [μs]
Błąd wyznaczenia czasu martwego licznika wyznaczam metodą różniczki zupełnej:
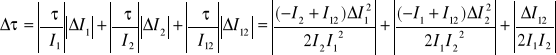
Przy czym błędy zliczania impulsów wyznaczam z zależności:
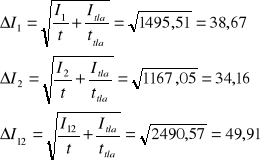
Zatem błąd wyznaczenia czasu martwego:
![]()
Ostatecznie więc wyznaczony przez nas czas martwy licznika wynosi:
τ = 289 ± 7 [μs]
Jest to czas, jaki licznik potrzebuje na zarejestrowanie kolejnej cząstki, a więc czas wygaszenia licznika.
Badanie statystycznego charakteru przemiany
promieniotwórczej.
Badań dokonywaliśmy za pomocą specjalistycznego sprzętu i dedykowanego oprogramowania. Poniżej przedstawione są wyniki dokonanych pomiarów otrzymane z komputera:
Liczba przemian: ki |
Liczba krotnności przemian n(ki) |
1 |
3 |
2 |
29 |
3 |
37 |
4 |
52 |
5 |
88 |
6 |
99 |
7 |
82 |
8 |
46 |
9 |
53 |
10 |
32 |
11 |
15 |
12 |
6 |
13 |
6 |
14 |
1 |
15 |
0 |
16 |
1 |
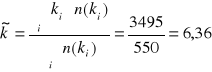
Aby zadecydować jaki rozkład prawdopodobieństwa będę testować jako najlepszy wyznaczam wartość średnią obserwowanej liczby przemian na podstawie zależności:
Jako, że otrzymana wartość średnia jest mniejsza od 20 przyjmuję hipotezę, że badany rozkład opisywany jest rozkładem Poissona. Jako, że rozpatrywany przeze mnie jest tylko jeden rozkład, przyjmuję z góry wartość poziomu ufności równą 99%. Dla takiego poziomu wyznaczona wartość graniczna statystyki wynosi 29,14 (dla 16-2=14 stopni swobody).
Przy pomocy testu χ2 sprawdzam słuszność postawionej hipotezy postępując według algorytmu postępowania zawartego w instrukcji. Poniższa tabela przedstawia poszczególne wyniki obliczeń, przy czym wykonane są one dla kśrednie = 6,36
|
|
|
|
|
|
|
|
|
1 |
3 |
3 |
-5,36 |
28,730 |
0,011 |
6,049 |
-3,049 |
1,537 |
2 |
29 |
58 |
-4,36 |
19,010 |
0,035 |
19,237 |
9,763 |
4,955 |
3 |
37 |
111 |
-3,36 |
11,290 |
0,074 |
40,782 |
-3,782 |
0,351 |
4 |
52 |
208 |
-2,36 |
5,570 |
0,118 |
64,844 |
-12,844 |
2,544 |
5 |
88 |
440 |
-1,36 |
1,850 |
0,150 |
82,481 |
5,519 |
0,369 |
6 |
99 |
594 |
-0,36 |
0,130 |
0,159 |
87,430 |
11,570 |
1,531 |
7 |
82 |
574 |
0,64 |
0,410 |
0,144 |
79,436 |
2,564 |
0,083 |
8 |
46 |
368 |
1,64 |
2,690 |
0,115 |
63,152 |
-17,152 |
4,658 |
9 |
53 |
477 |
2,64 |
6,970 |
0,081 |
44,627 |
8,373 |
1,571 |
10 |
32 |
320 |
3,64 |
13,250 |
0,052 |
28,383 |
3,617 |
0,461 |
11 |
15 |
165 |
4,64 |
21,530 |
0,030 |
16,411 |
-1,411 |
0,121 |
12 |
6 |
72 |
5,64 |
31,810 |
0,016 |
8,698 |
-2,698 |
0,837 |
13 |
6 |
78 |
6,64 |
44,090 |
0,008 |
4,255 |
1,745 |
0,716 |
14 |
1 |
14 |
7,64 |
58,370 |
0,004 |
1,933 |
-0,933 |
0,450 |
15 |
0 |
0 |
8,64 |
74,650 |
0,001 |
0,820 |
-0,820 |
0,820 |
16 |
1 |
16 |
9,64 |
92,930 |
0,001 |
0,326 |
0,674 |
1,395 |
SUMA: χ2 = 22,399 |
||||||||
Jako, że kśrednie = 6,36 jest mniejsze od 20 przyjęliśmy hipotezę, że badany rozkład jest rozkładem Poissona. Dodatkowo, założyliśmy poziom ufności równy 99% (wartość graniczna χ2=29,14). Ostatecznie ponieważ wyznaczona wartość statystyki χ2=22,4 jest mniejsza od wartości granicznej - przyjmuję hipotezę jako poprawną.
5
1
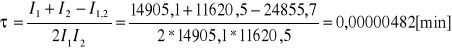
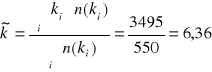
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
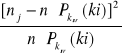
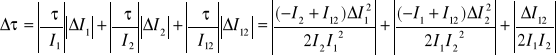
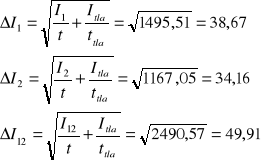
![]()
Wyszukiwarka