Paweł Panek

WIMIR gr 23B

Projektowanie liniowych układów dynamicznych w przestrzeni stanów, sterowalność i obserwowalność liniowych układów dynamicznych

Cele:

- modelowanie układów dynamicznych w przestrzeni stanów,

- badanie sterowalności i obserwowalności liniowych układów dynamicznych.

1. Modelowanie układu dynamicznego.

- wielkość wejściowa: Uw

- wielkość wyjściowa: Uc

- R=10Ω, L=1H, C=2F

,
,

Otrzymujemy na bloku Y wykres:

2. Modelowanie układu dynamicznego w przestrzeni stanów.

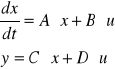
gdzie: x1=i , x2= Uc , y= UL , u= UW

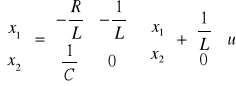
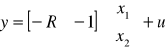
Po wpisaniu odpowiednich wartości liczbowych macierzy do bloku State-Space otrzymujemy na bloku Y2 taki sam wykres jak na Y.

3. Badanie sterowalności.

W programie Matlab za pomocą komendy Qs=ctrb(A,B), otrzymujemy macierz sterowalności (po wprowadzeniu odpowiednich wartości liczbowych do macierzy A i B):

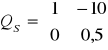
Za pomocą komend rank(A) i rank(Qs), dostajemy odpowiednio wartości rzędów macierzy A i Qs. W obu przypadkach rząd ten wyniósł 2. Na tej podstawie, że rzędy tych macierzy są sobie równe, możemy stwierdzić iż układ jest stabilny.

4. Badanie obserwowalności.

Podobnie jak wyżej: Q0=obsv(A,C) - otrzymujemy macierz obserwowalności:

,

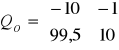
której rząd wyniósł 2 (równy rzędowi macierzy A), a więc układ jest obserwowalny!

---