Ćwiczenie 16	Nowak Michał	09.12.2003 r.	Zespół: 1 Grupa: 21
				Wydział Fizyki Tech. i Modelowania Komp.

Wyznaczanie naprężeń za pomocą tensometru oporowego.

1. Wstęp teoretyczny:

Tensometr oporowy jest elementem służącym do wyznaczania wydłużeń względnych występujących w elementach konstrukcji. Zmiany oporu elektrycznego tensometru pozwalają na obliczenie wydłużenia względnego, które jest proporcjonalne do naprężenia w odkształconym materiale.

gdzie E jest modułem Younga.

Najczęściej spotykaną postacią tensometru oporowego jest drucik metalowy (2r=0,025 mm) wklejony między dwa cienkie paski papieru. Jego opór wynosi zazwyczaj około 100Ω. Tensometr naklejamy klejem acetonowym na oszlifowaną i oczyszczoną powierzchnię badanego elementu i suszymy około doby. Poddajemy następnie materiał deformacji, np. rozciąganiu w kierunku włukien tensometru: druciki ulegają wydłużeniu, ich opór elektryczny się zmienia.

Ze wzoru:

na opór drutu widać, że na zmianę oporu tensometru składają się: zmiana długości drutu oporowego
, zmiana pola przekroju
i zmiana oporu właściwego odkształconego drucika. Doświadczenie mówi, że stosunek:

jest dla danego tensometru wielkością stałą, zależną od materiału tensometru.

2. Metoda pomiaru:
   Dla znalezienia wydłużenia względnego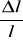
   należy wyznaczyć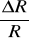
   . Do pomiaru oporu stosujemy obwód elektryczny zwany mostkiem Wheatstone'a. W jedną gałąź mostka włączamy tensometr czynny R₁, drugą, jako opór znany taki sam tensometr, przyklejony takim samym klejem na takim samym podłożu, tzw. Tensometr kompensacyjny R₂. Postępowanie to ma na celu:

1. wyeliminowanie wpływu temperatury na opór tensometru, wpływu na ogół silniejszego niż wpływ naprężeń mechanicznych,

2. wyeliminowanie zmiany oporu tensometru spowodowanej skurczem kleju.

Tensometr czynny (jego opór R₁) przyklejony jest do płaskownika, w którym będziemy badać naprężenie. Zaczynamy pomiar, gdy płaskownik spoczywa na stole - jest nie obciążony. Poddajemy następnie materiał odkształceniu. W tym celu mocujemy go w uchwycie. Ponieważ zmienia się opór tensometru przyklejonego do odkształconego płaskownika o
, równowaga mostka zostaje zakłócona i pojawia się prąd
płynący przez galwanometr.

Aby ponownie uzyskać równowagę, przesuwamy styk w nowe położenie
. Przy
jest spełniona proporcja:

gdzie
oznacza opór odcinka drutu oporowego o długości:
. Łatwo go obliczyć ze wzoru:

mając opór całkowity drutu
i jego długość (L=1000 mm):

Przy założeniu, że: R₁= R₂, zaś : R₃ = R₄ = R₀ + 0,5 R₅, równanie nasze przybierze postać:

Pamiętając, że ΔR₃ << R₃, i zaniedbując wyrazy z ΔR₃², przekształcamy nasze równanie do postaci:

stąd:

Ze wzoru:

wynika, że wydłużenie względne tensometru czynnego jest równe:

Podstawiając do wzoru:

zależności:

i

dostajemy ostateczny wzór na naprężenie mierzone tensometrem:

III. Wykonanie ćwiczenia i opracowanie wyników:

Celem ćwiczenia jest wyznaczenie naprężenia σ w oznaczonym miejscu zginanego płaskownika stalowego.

Parametry tensometru:

• stała tensometru: k = 2,1

• opór boczny: R₀ = 50 Ω

• opór drutu: R₅ = 0,35 Ω

Moduł Younga:

Długość drutu oporowego: L = 1 m

Początkowe położenie styku:

r m	xi m	Δ xi = | xi - x0 | m	σ N/m^2
obciążenie własne belki	0,467	0,02	2,760 ⋅ 10^7
0,28	0,476	0,029	4,002 ⋅ 10^7
0,38	0,485	0,038	5,244 ⋅ 10^7
0,48	0,490	0,043	5,934 ⋅ 10^7
0,58	0,495	0,048	6,624 ⋅ 10^7
0,68	0,499	0,052	7,176 ⋅ 10^7
0,78	0,504	0,057	7,866 ⋅ 10^7
0,88	0,509	0,062	8,556 ⋅ 10^7

Naprężenia zostały wyliczone ze wzoru:
w którym ΔR₃ dane jest wyrażeniem
,a R₃ = R₄ = R₀ + 0.5 R₅, wiec ostatecznie:

Obliczam niepewność maksymalną σ dla jednego pomiaru (np. dla obciążenia własnego belki):

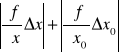
Zadanie 2.

Obliczam naprężenie w tym samym miejscu belki, korzystając ze wzoru teorii sprężystości dane wzorem :

σ =

, gdzie

M=M₁+ M₂

M_1=
, M₂=

σ =

m		M1 m	σ N/m^2
0,1		17,03	7,141⋅10^7
0,2		15,06	6,401⋅10^7
0,3		13,10	5,686 ⋅10^7
0,4		11,14	5,062⋅10^7
0,5		9,18	4,234⋅10^7
0,6		7,22	3,508⋅10^7
0,7		5,25	2,778⋅10^7
0,8		3,29	2,052⋅10^7
0,9	1,33		1,337⋅10^7

1

---