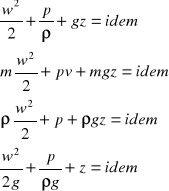1.Z jakiego równania wynika równanie:

wynika z równania EULERA {ruchu płynu,wirowy}

załozenia:

ruch jest ustalony

δ=idem płyn nieścisliwy

otrzymujemy równanie:

korzystam z równań:

grad u=Fm -

u=gz -

2. ekwipotencjalne powierzchnie płynu

-powierzchnia swobodna cieczy

-powierzchnia rozdziału dwóch cieczy o róznych gestosciach nie mieszajacych się

właściwości powierzchni ekwipotencjalnych to:

-gestosc na powierzchni ekwipotencjalnych się nie zmieniaja

-cisnienie również jest stałe

Aby okreslic powierzchnie ekwipotencjalne:

-δ(adx+gdz}=dp

u=(xyz)=idem - du=0 --dp=0

Rownanie ekwipotencjalne to inaczej powierzchnie izobaryczne (tworza się tzw powierzchnie stalego cisnienia)

3.siły zwiazane z masa płynu

sily zwiazane z masa plynu to sily masowe .W sklad sil masowych wchodza :

a}grawitacyjne,b}bezwladnosci,c}elektromagnetyczne

cechuja się one tym ze wartosci ich sa proporcjonalne do ilosci substancji badanego plynu.

4.wielosci charakteryzujace procesy przepływu:

różnice ciśnień,predkosc,temperatura,lepkość,entalpia.

5.z jakiego równania pochodzi to równanie:

jest to równanie naviera-stockesa i wynika z rownania naviera-stockesa:

założenia:

Wz=0, W=Wx -przepływ tylko w jednym kierunku

-przepływ ustalony

-przepływ jedt jednostkowy

Fmx=0 , Fmy=0 ,
-przepływ jest dwuwymiarowy

6. co oznacza funkcja dysypacji energi (Φ)

funkcja dysypacji energi jest funkcja rozproszenia energi, rozumiane jest jedno ciepło ,inaczej mowiac:to opory przepływu )wszystko to jest zwiazane z rozproszeniem}

t-{tał)-naprezenia styczne na poszczegolnych kierunkach.

w-predkosc płynu na poszczegolnych kierunkach

Funkcja dyscypacji -funkcja rozproszenia energi tzn ta czesc pracy sil powierzchniowych która ulega przeksztalceniu na energie kinetyczna ale ma energie wewnetrzna płynu.

7.co to za równanie:

jest to równanie energi

Równaie ogólne energi:

rozpisujemy rownanie na kierunki:

zakładamy że:

otrzymujemy:

8. Jakie mamy korzysci z korzystania z liczb kryterialnych w mechnice.:

Liczby kryterialne:wynikaja z twiedzen teoripodobienstwa , pozwalaja na stworzenie i badanie modeli rzeczywistych obiektow. Spełniajac warunki teorii podobienstwa (3 litery kryterialne) można poznac rzeczywwiste wielkosci charakteryzujace obiekt na podstawie wykonanego modelu. Sa bezwymiarowe i uniwersalne:

Jeżeli :
- stały stosunek

Np.:

Jeśli kiedys będę dokonywał badań i będę miał równania opisujące model,to możemy przejsc na model rzeczywisty. Należy bowiem uwzglednic liczby Reynoldsa,Eulera,Freuda

9. od jakich wielkosci zalezy predkosc wwypływu cieczy przez otwór ostrokrawedziowy ze zbiornika:

predkosc wyplywu dobieramy ze wzoru:

a wiec od wspolczynnika α definiowanego jako:

α=ψ*φ gdzie:

ψ-Wz/Wzt-wspolczynnik uwzgledniajacy lepkosc

φ=Azp/Az -wspolczynnik przewezenia strugi

10.Równanie

jest to rownanie momentow pedow ,reakcji siły oddzialywania plynu na scianki dla urzadzen wirnikowych.

Załozenia:

a}pole predkosci jednorodne,

b}grubosc profilu=0

c}m1=m2=m-nie ma odprowadzenia plynow lub doprowadzenia w przewodach 1 i 2

d}wirni idealny(nieskonczona ilosc łopatek)

e)plyn doskonały

f)musi bys spelnione rownanie ciagłosci przepływu

g)przepływ ustalony

h)grubośc łopatek równa 0

11.siła nośna dowolnego profilu

Siłe nośna dowolnego profilu wyraza się wzorem:

jej wartosc jest zalezna od:

c-wspolczynnik siły nosnej, A. Gestosci, kwadratu predkosci.

12.straty cisnienia przy przeplywie.

Straty cisnienia przy przeplywie wynikaj ze strat cisnienia spowodowanych tarciem oraz strat cisnienia w oporach miejscowych.

λ-wspl.oppru

l-dlug.rurociagu

ρ-gestosc plynu

w-predkosc

d-srednica rurociagu

ζ-wspol.strat miejscowych

13.energia płynu-

jest suma energi wewnetrznej, kinematycznej i proporcjonalnej do kwadratu predkosci . energia wewnetrzna wiaze się z energia ruchu cieplnego czastek i atomow ciala. Zmiany rodzaju energi wewnatrz czasteczkowej i wewnatzratomowej sa pomijane.

Zasada zachowania energi odniesiona do obszaru plynnego wymaga aby przyrost energi plynu zawartego w tym obszarze był rowny sumie skladowej:

-pracy wykonanej przez sily mechaniczne

-energi cieplnej utworzonej wewnatrz obszaru plynnego

energi cieplnej dostarczonej do obszaru poprzez przewodzenie ciepla powierzchni plynnej

14.Rownanie rownowagi płynu

TWIERDZENIE GAUSA-OSTROGADZKIEGO

warunki rownowagi plynu doskonalego-elementarna energia cisnienieniowa w dowolnym punkcie plynu bedaca w rownowadze ma nastepujace cechy:

-modul o ds. niezaleznie od przestrzennej orirntacji elementarnej powierzchni ds.

-kierunek normalny do ds.

zwrot ku powierzchni ds.

w dowolnym punkcie obszary plynne w stanie rownowagi. Wektor siły masowej jest prostopadły do powierzchni izobarycznej przechodacej przez ten punkt.

Skladowa sily cisnieniowej w plynie w dowolnym kierunku jest proporcjonalna do skladowej wektora sily masowej w tym kierunku.

15.paradoks hydrostatyczny

F=p*A=ro*g*z*A=ro*g*V=mg=G

Parcie na wycinek plaskiej scianki zbiornika jest rowne iloczynowi pola powierzchni tego wycinka przez panujace cisnienie w jego srodku ciezkosci. Wynika z tego paradoks hydrostatyczny odnoszacy się do parcia na poziome dna zbiornika.

Zalezy ono od :

-pola powierzchni dna

-odleglosci od zwierciadla cieczy

-nie zalezy od obietosci cieczy w zbiorniku

16, Wyprowadzic wzor na pochodna substancjonalna

-funkcja ogólna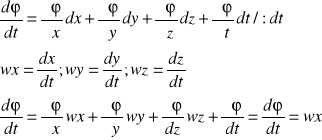

17. Rownanie ruchu płynu

ogolne rownanie ruchu płynu:

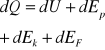
dU-roznica energi wewnetrzbej

dEk-roznica energi kinetycznej

dEp-roznica energi potencjalnej

dEf-zmiana energi dzialajacym siłom powierzchniowym.

18.Rozszyfrowac człony

jest to rownanie nawiera -stokesa w formie wektorowej

Fm-siły masowe na kierunkach x,y,z,

-zmiany predkosci w czasie na x,y,z

1/ρ grad p-od sil powierzchniowych na x,y,z

-od zmian predkosci a kierunkach x,y,z

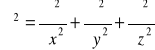
19. Rownanie

jest to rownanie ciaglosci przepływu płynu

otrzymujemy je z ogolnego rownania:

m=A*w*ρ

rozpisujemy na kierunki:

x=ρWxdydz

y=ρWydxdz

z=ρWzdxdy

otrzymujemy zaleznosc w postaci rozniczkowej:

nastepnie:

i otrzymujemy:

20.postacie równania BERNOULIEGO:

---